Вычисление пределов функции с помощью замены бесконечно малых на эквивалентные.
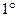 Функция называется
Функция называется 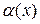 бесконечно малой при
бесконечно малой при 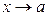 (или в точке
(или в точке 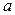 ), если
), если 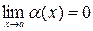 .
.
Пусть 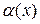 и
и 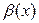 - две бесконечно малые функции при
- две бесконечно малые функции при 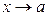 .
.
1) Если 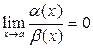 , то
, то 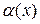 называются бесконечно малой более высокого порядка чем
называются бесконечно малой более высокого порядка чем 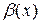 (при
(при 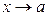 );
);
2) Если 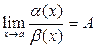 , то
, то 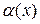 и
и 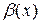 называются бесконечно малыми одного порядка (при
называются бесконечно малыми одного порядка (при 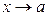 );
);
3) Если 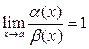 , то
, то 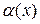 и
и 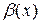 называются эквивалентными бесконечно малыми (при
называются эквивалентными бесконечно малыми (при 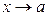 ). Эквивалентность обозначается так:
). Эквивалентность обозначается так: 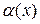 ~
~ 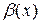 при
при 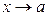 .
.
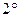 Приведем таблицу эквивалентных бесконечно малых функций при
Приведем таблицу эквивалентных бесконечно малых функций при 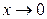 :
:
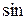
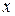 ~
~ 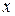 ,
,  ~
~ 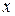 ,
, 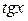 ~
~ 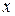 ,
, 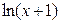 ~
~ 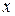 ,
, 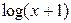 ~
~ 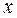
 ,
,
 ~
~ 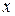 ,
, 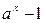 ~
~ 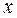
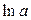 ,
, 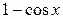 ~
~ 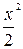 ,
, 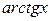 ~
~ 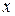 ,
,  ~
~ 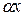 ,
,
Пример 5. Найти пределы:
а) 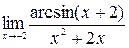 , б)
, б) 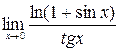 .
.
Решение. а) 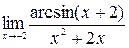 =
= 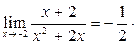
б) 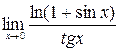 =
= 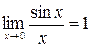 .
.
Пример 6. Найти предел:
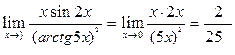 .
.
Контрольные вопросы:
1. Понятие последовательности.
2. Понятие предела последовательности
4. Определение предела функции.
5. Свойства пределов.
6. Два замечательных предела.
7. Понятие эквивалентных бесконечно малых функций.
8.Вычисление пределов функции с помощью замены бесконечно малых на эквивалентные.
Задания .
1. Вычислить пределы:
а) 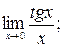 б)
б) 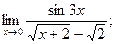 в)
в) 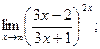 г)
г) 
2.Найти пределы последовательностей:
1) 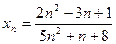 ; 2)
; 2) 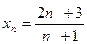 ; 3)
; 3) 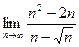 ;
;
4) 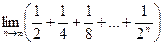 ; 5)
; 5) 
3. Пользуясь методом замены бесконечно малых эквивалентными вычислить следующие пределы:
а) 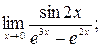 б)
б) 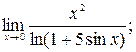 в)
в) 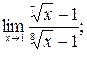
Тема 9.
Непрерывность функции
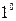 Функция
Функция 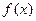 называется непрерывной в точке
называется непрерывной в точке 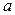 , если:
, если:
1) эта функция определена в некоторой окрестности точки 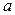 ;
;
2) существует 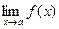 ;
;
3) этот предел равен значению функции в точке 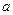 , т.е.
, т.е. 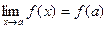 ,
,
Обозначая 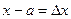 (приращение аргумента) и
(приращение аргумента) и 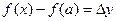 , (приращение функции), условие непрерывности можно записать так:
, (приращение функции), условие непрерывности можно записать так: 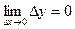 , т.е. функция
, т.е. функция 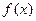 непрерывна в точке
непрерывна в точке 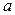 тогда и только тогда, тогда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
тогда и только тогда, тогда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т.п.), то она называется непрерывной в этой области.
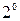 Функция
Функция  называется непрерывной в точке
называется непрерывной в точке  справа, если выполняется условие
справа, если выполняется условие 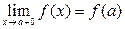 (когда
(когда 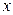 стремится к
стремится к 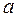 справа, оставаясь больше
справа, оставаясь больше 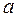 ).
).
Если 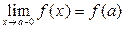 , то говорят, что функция
, то говорят, что функция  непрерывна слева (когда
непрерывна слева (когда 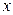 стремится к
стремится к 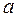 слева, оставаясь меньше
слева, оставаясь меньше 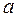 ).
).
.
Если  непрерывна в точке
непрерывна в точке 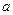 слева и справа, то она непрерывна в этой точке.
слева и справа, то она непрерывна в этой точке.
 Функция
Функция  имеет разрыв в точке
имеет разрыв в точке 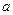 , если она определена в сколь угодно близких точках к
, если она определена в сколь угодно близких точках к 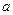 , но в самой точке
, но в самой точке 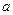 нарушается хотя бы одно из условий непрерывности функции.
нарушается хотя бы одно из условий непрерывности функции.
Конечным разрывом или разрывом первого рода называется разрыв функции  в точке
в точке 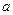 , если существуют конечные односторонние пределы
, если существуют конечные односторонние пределы
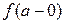 и
и 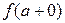 .
.
Скачком функции  в точке
в точке 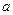 называется разность его односторонних пределов
называется разность его односторонних пределов 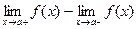 , если они различны.
, если они различны.
Если 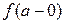 =
= 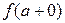 , то точка
, то точка 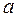 называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
Все другие случаи разрыва функции называются разрывами 2-го рода.
Если хотя бы один из указанных односторонних пределов окажется бесконечным, то разрыв функции называется бесконечным.
Пример 1.
Исследовать функцию на непрерывность; непрерывность справа и слева и установить характер точек разрыва, где

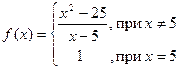
Решение. При 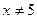 можно сократить на
можно сократить на 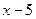 .
.
Следовательно,  при
при 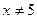 . Легко
. Легко
видеть, что 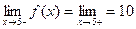 . Значит, при
. Значит, при 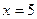 функция будет разрывной, так как предел функции не равен значению функции в этой точке.
функция будет разрывной, так как предел функции не равен значению функции в этой точке.
Пример 2. Исследовать на непрерывность функцию
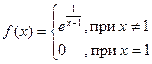
Решение. Найдем односторонние пределы в точке 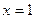 , т.е.
, т.е.
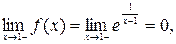
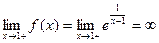 .
.
В точке 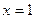 функция
функция 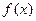 имеет разрыв 2 рода. Так как предел слева в точке
имеет разрыв 2 рода. Так как предел слева в точке 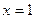 равен значению функции в этой точке, то функция непрерывна слева в точке
равен значению функции в этой точке, то функция непрерывна слева в точке 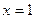 . При остальных значениях
. При остальных значениях 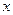 функция непрерывна (по теореме непрерывности суперпозиции функций).
функция непрерывна (по теореме непрерывности суперпозиции функций).
Пример 3. Доказать непрерывность функции 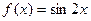 .
.
Решение. Пусть 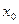 - произвольное значение на числовой прямой.
- произвольное значение на числовой прямой.
Найдем 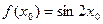 и составим разность
и составим разность
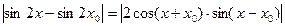
Оценим полученное выражение в правой части по абсолютной величине
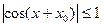 ,
,
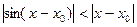 .
.
Итак, отмечаем, что
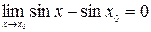 .
.
Контрольные вопросы
1. Определение непрерывной функции в точке.
2. Разрыв функции в точке. Классификация разрывов.
3. Свойства непрерывных функций.
Задания.
1) Показать, что при 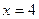 функция
функция  имеет разрыв.
имеет разрыв.
2) Найти точки разрыва функции 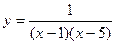 .
.
3) Каков характер разрыва функции 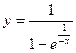 в точке
в точке 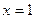 .
.
4) Исследовать на непрерывность функции
а) 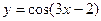 ; б)
; б) 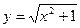
Тема 10
Производная функции
 Пусть функция
Пусть функция 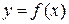 определена на интервале
определена на интервале 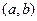 .Определим:
.Определим:
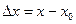 - приращение аргумента
- приращение аргумента 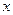 в точке
в точке  , а
, а
 - приращение функции в точке
- приращение функции в точке 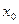 .
.
Если существует конечный предел
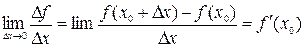 ,
,
то он называется производной функции  в точке
в точке 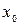 .
.
Значение производной 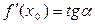 -есть угловой коэффициент касательной к графику функции
-есть угловой коэффициент касательной к графику функции 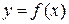 в точке, абсцисса которой есть
в точке, абсцисса которой есть 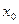
Если 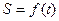 - закон прямолинейного движения точки, то первая производная пути по времени
- закон прямолинейного движения точки, то первая производная пути по времени 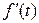 -есть скорость этого движения.
-есть скорость этого движения.
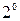 . Основные правила дифференцирования.
. Основные правила дифференцирования.
Пусть 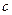 - некоторая постоянная,
- некоторая постоянная, 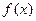 ,
, 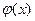 - функции, имеющие производные.
- функции, имеющие производные.
Справедливы следующие правила дифференцирования:
1. 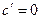 ; 2.
; 2. 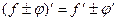 ; 3.
; 3. 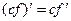 ; 4.
; 4. 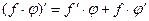 ;
;
5. 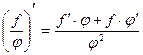 ;
; 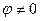 .
.
6. Производная сложной функции.
Если функции 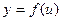 и
и 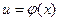 имеют конечные производные, то
имеют конечные производные, то
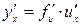
7. Дифференцирование функции, заданной параметрически..
Пусть зависимость между 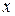 и функцией
и функцией  задана параметрически в виде двух уравнений
задана параметрически в виде двух уравнений
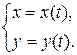
где 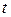 -вспомогательная переменная, называемая параметром.
-вспомогательная переменная, называемая параметром.
Производная 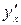 функции, заданной параметрически определяется по правилу
функции, заданной параметрически определяется по правилу
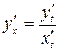 , или
, или 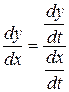 .
.
8. Производная обратной функции.
Пусть функция  в некоторой окрестности точки
в некоторой окрестности точки 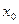 возрастает (или убывает) и является непрерывной. Пусть кроме того, функция
возрастает (или убывает) и является непрерывной. Пусть кроме того, функция  дифференцируема, в точке
дифференцируема, в точке 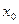 и производная
и производная 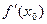 отлична от нуля. Тогда обратная функция
отлична от нуля. Тогда обратная функция  определена в некоторой окрестности соответствующей точки
определена в некоторой окрестности соответствующей точки 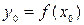 , дифференцируема в этой точке и имеет в этой точке производную, равную
, дифференцируема в этой точке и имеет в этой точке производную, равную 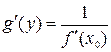 .
.
9. Производная функции  ,
, 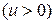 , где
, где 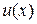 и
и  суть функции от
суть функции от 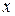 , имеющие в данной точке производные
, имеющие в данной точке производные 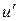 и
и  есть:
есть:
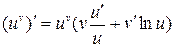
Пример 1. Исходя из определения производной, найти производную функции 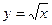 .
.
Решение. Зададим приращение 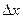 , такое, что
, такое, что 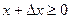 .
.
Тогда
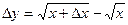 ;
;
Поэтому
 ;
;
Переходим к пределу при 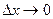 :
:
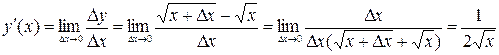 ;
;
т.е. 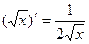 .
.
Пример 2. Исходя из определения производной функции, найти производную функции 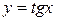 .
.
Решение. Находим
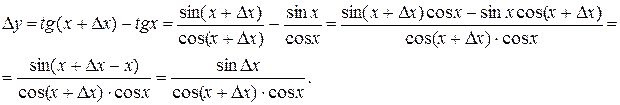
Откуда
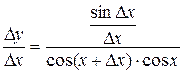
и, следовательно
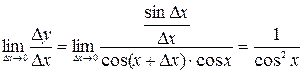 .
.
Итак, 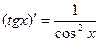 .
.
 . Формулы дифференцирования основных элементарных функций:
. Формулы дифференцирования основных элементарных функций:
1. 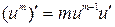 ; 11.
; 11. 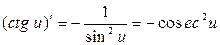 ;
;
2.  ; 12.
; 12. 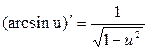 ;
;
3. 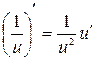 ; 13.
; 13. 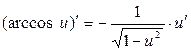 ;
;
4. 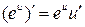 ; 14.
; 14.  ;
;
5. 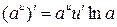 ; 15.
; 15. 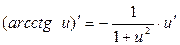 ;
;
6. 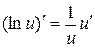 ; 16.
; 16. 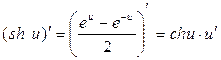 ;
;
7. 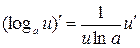 ; 17.
; 17. 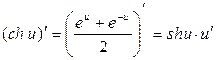 ;
;
8. 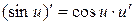 ; 18.
; 18. 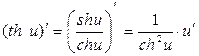 ;
;
9. 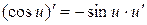 ; 19.
; 19. 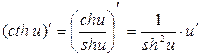 .
.
10. 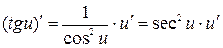 ;
;
Пример 3. Найти производную функции 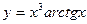 .
.
Решение.
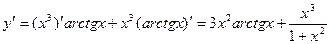 .
.
Пример 4. Найти производную 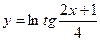 .
.
Решение. Берем производную от 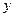 как сложной функции
как сложной функции
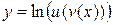 , где
, где 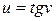 ,
, 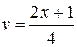 .
.
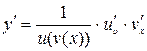 , где
, где 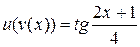 ,
,
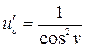 ;
; 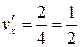
Итак,
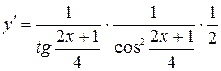 .
.
Пример 5. Найти производную функции 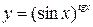
Решение. Имеем 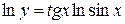 , откуда
, откуда
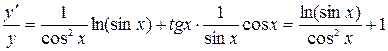 ,
,
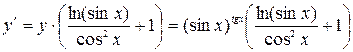 .
.
Пример 6. Найти 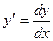 , если
, если 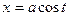 ,
, 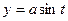 .
.
Решение. Имеем
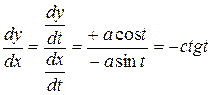
Пример 7. Найти производную 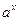 .
.
Решение. Показательная функция 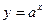 , определена на бесконечной прямой и служит обратной для логарифмической функции
, определена на бесконечной прямой и служит обратной для логарифмической функции 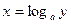 .
.
Согласно вышеуказанному утверждению, функция 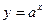 дифференцируема в любой точке
дифференцируема в любой точке 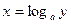 и для ее производной справедлива формула
и для ее производной справедлива формула 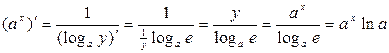 .
.
Итак, 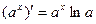 .
.
Пример 8. Вычислить производную 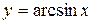 .
.
Решение. Функция 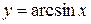 , определенная на интервале
, определенная на интервале 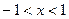 , служит обратной для функции
, служит обратной для функции 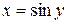 , определенной на интервале
, определенной на интервале 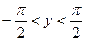 . Пользуясь правилом дифференцирования обратной функции, получим:
. Пользуясь правилом дифференцирования обратной функции, получим:
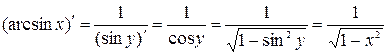 .
.
Мы взяли перед корнем знак +, т.к. 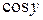 положителен всюду на интервале
положителен всюду на интервале 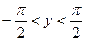 .
.
Итак  .
.
Понятие дифференциала.
 Пусть функция
Пусть функция 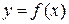 имеет в точке
имеет в точке 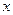 конечную производную
конечную производную 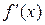 , тогда ее приращение можно записать в виде
, тогда ее приращение можно записать в виде
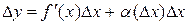 ,
,
где 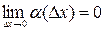 .
.
Главная, линейная относительно 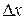 часть
часть 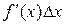 приращения функции называется дифференциалом функции и обозначается
приращения функции называется дифференциалом функции и обозначается 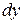 :
:
 .
.
При 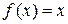 , получим
, получим 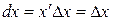 , поэтому дифференциал функции
, поэтому дифференциал функции 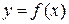 примет вид
примет вид
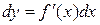 .
.
 Основные свойства дифференциала
Основные свойства дифференциала
1)  где
где 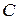 = const,
= const,
2) 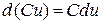
3) 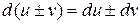 ,
,
4) 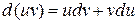 ,
,
5) 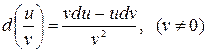
6) 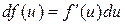 .
.
 Применение дифференциала для приближенных вычислений.
Применение дифференциала для приближенных вычислений.
При достаточно малых 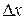 приращение функции приближенно равно ее дифференциалу, т. е.
приращение функции приближенно равно ее дифференциалу, т. е. 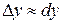 и
и
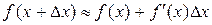 .
.
Пример 9. Найти дифференциал функции  .
.
Решение. Найдем производную данной функции 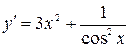 .
.
Следовательно, по определению дифференциала функции получим
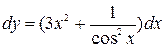 .
.
Пример1 0. Вычислить с помощью дифференциала приближенное значение 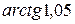
Решение . Рассмотрим функцию  . Пологая
. Пологая 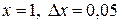 и применяя формулу
и применяя формулу 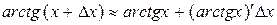 , получим
, получим
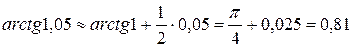 .
.
3.Производные высших порядков.
Производной второго порядка (второй производной) функции  называется производная от производной
называется производная от производной 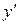 . Вторая производная обозначается так:
. Вторая производная обозначается так: 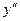 , или
, или 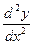 , или
, или 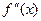 .
.
Если 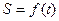 - закон прямолинейного движения точки, то вторая производная пути по времени
- закон прямолинейного движения точки, то вторая производная пути по времени 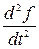 есть ускорение этого движения.
есть ускорение этого движения.
Аналогично производная третьего порядка функции  есть производная производной второго порядка
есть производная производной второго порядка  и т.д., производной n-го порядка от функции
и т.д., производной n-го порядка от функции  называется производная от производной
называется производная от производной 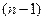 -го порядка
-го порядка  . Обозначается n-я производная так:
. Обозначается n-я производная так: 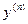 или
или 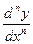 , или
, или 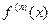 .
.
Пример 10. Дана функция  .
.
Найти: 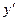 ,
, 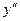 ,
,  , …
, …
Решение.
 ;
; 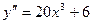 ;
;
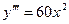 ;
; 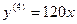 ;
; 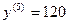 ;
;
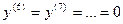 .
.
Пример 11. Дана функция 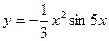
Найти: 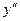 .
.
Решение. 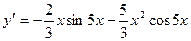 ,
,
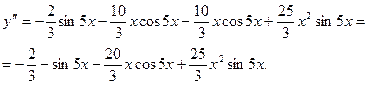
Контрольные вопросы.
Производная функции.
2.Основные правила дифференцирования.
3.Производная обратной функции.
4.Формулы дифференцирования основных элементарных функций.
5.Понятия дифференциала функции.
6.Применение дифференциала к приближенным вычислениям.
7.Производные высших порядков.
Задания.
1. Пользуясь определением производной вычислить производные следующих функций:
1) 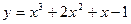 ;
;
2)  .
.
2. Найти производные и дифференциалы следующих функций
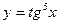 ;
; 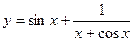 ;
; 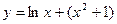 ;
; 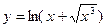 ;
;
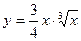 ;
; 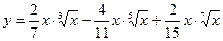 ;
; 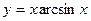 ;
;
 ;
; 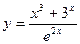 .
.
3.Найти производные функций:
1) 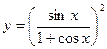 ;
;
2) 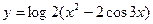 ;
;
3) 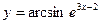 ;
;
4)  .
.
4.Найти 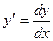 ,
,
1) если 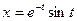 ,
, 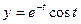 ;
;
2) если 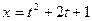 ,
, 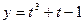 ;
;
3) если 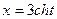 ,
, 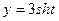 .
.
5.Вычислить с помощью дифференциала приближенные значения
 ,
, 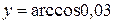 ,
, 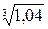 ,
, 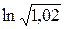 .
.
6.Найти производные
1)обратных тригонометрических функций
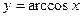 ;
; 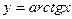 ;
; 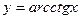 ;
; 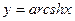 ;
; 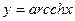 .
.
2)  обратную к
обратную к 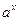 .
.
7. Найти 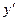 ,
, 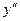 ,
,  , …,
, …, 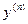 для функций:
для функций:
1) 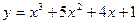 . 2)
. 2)  . 3)
. 3)  . 4)
. 4) 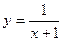 .
.
Тема 11
1.Теоремы Ролля, Лагранжа, Коши. Фрмула Тейлора.
 Теорема Ролля. Если функция
Теорема Ролля. Если функция 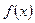 непрерывна на отрезке
непрерывна на отрезке 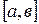 , дифференцируема в интервале
, дифференцируема в интервале 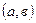 и
и 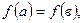 то в интервале
то в интервале 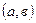 найдётся хотя бы одно значение
найдётся хотя бы одно значение  , при котором
, при котором 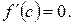
 Теорема Лагранжа (о конечном приращении). Если функция
Теорема Лагранжа (о конечном приращении). Если функция 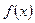 непрерывна на отрезке
непрерывна на отрезке 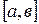 , дифференцируема в интервале
, дифференцируема в интервале 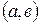 , то в этом интервале найдётся хотя бы одно значение
, то в этом интервале найдётся хотя бы одно значение 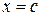 , при котором выполняется равенство
, при котором выполняется равенство 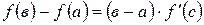 (геометрический смысл: касательная в точке
(геометрический смысл: касательная в точке  параллельна секущей АВ).
параллельна секущей АВ).
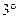 Теорема Коши. Если функции
Теорема Коши. Если функции 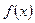 и
и  непрерывны на отрезке
непрерывны на отрезке 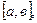 и дифференцируемы в интервале
и дифференцируемы в интервале 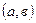 , причём
, причём 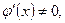 то в этом интервале найдётся хотя бы одно значение
то в этом интервале найдётся хотя бы одно значение 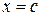 , при котором
, при котором 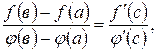 где
где 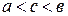 .
.
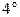 Формула Тейлора. Если функция
Формула Тейлора. Если функция 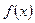 имеет в точке
имеет в точке 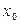 все производные до порядка
все производные до порядка 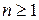 включительно, то
включительно, то
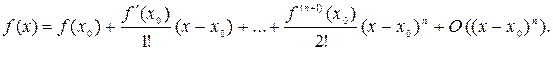
Это соотношение называется формулой Тейлора с остаточным членом в форме Пеано.
При 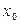 = 0 получаем частный случай формулы Тейлора-формулу Маклорена
= 0 получаем частный случай формулы Тейлора-формулу Маклорена 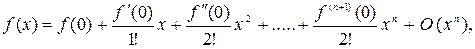
Приведем разложение некоторых функций по формуле Маклорена:
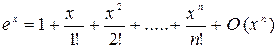 ,
,
 ,
,
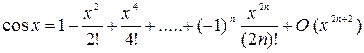
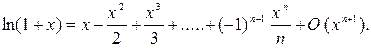
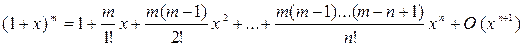
Пример 1. Выполняется ли теорема Ролля для функции 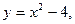
если а=-3; в=3. Найти значение  .
.
Решение. Так как функция 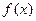 непрерывна и дифференцируема при всех значениях х и её значения на концах отрезка
непрерывна и дифференцируема при всех значениях х и её значения на концах отрезка 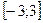 равны
равны 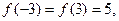 Следовательно, условия теоремы Ролля на этом отрезке выполняются. Значение
Следовательно, условия теоремы Ролля на этом отрезке выполняются. Значение  определяем из уравнения
определяем из уравнения 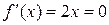 , т.е.
, т.е. 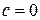 .
.
Пример 2. На дуге АВ кривой 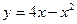 найти точку М, в которой касательная параллельна хорде АВ, если А(1, 3) и В(3, 3).
найти точку М, в которой касательная параллельна хорде АВ, если А(1, 3) и В(3, 3).
Решение. Функция 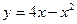 непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 существует значение х=
непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 существует значение х=  , удовлетворяющее равенству:
, удовлетворяющее равенству:
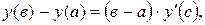
где 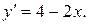
Подставив соответствующие значения, получим
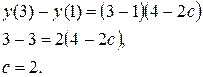
Отсюда 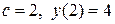 . Таким образом, точка М имеет координаты М(2; 4).
. Таким образом, точка М имеет координаты М(2; 4).
Пример 3. Проверить теорему Коши для функции 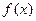 =х3 и
=х3 и 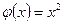 и найти с.
и найти с.
Решение . Из формулы Коши имеем
 , т.е.
, т.е. 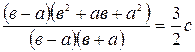 .
.
Отсюда, получим 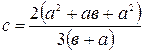 .
.
Пример 4. Разложить функцию 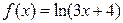 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 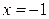 .
.
Решение. Представим, данную функцию в виде
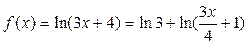 .
.
Далее воспользуемся формулой  .
.
Будем иметь
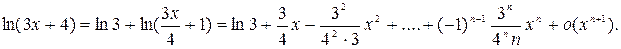
Пример 5. Вычислить предел, используя разложение по формуле Тейлора
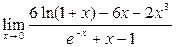 .
.
Решение. Так как
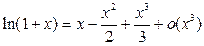 и
и 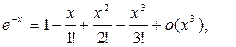 то получим
то получим
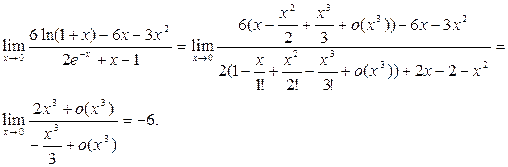
Контрольные вопросы.
1. Теоремы Ролля, Лагранжа, Коши.
2.Формула Тейлора. Формула Маклорена.
3.Разложение элементарных функций в ряд Маклорена.
Задания.
1. Применима ли теорема Ролля к функции 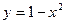 на отрезке
на отрезке  . Пояснить графически.
. Пояснить графически.
2. Проверить теорему Лагранжа и найти с для функций: а) 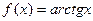 на отрезке
на отрезке 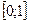
б)  на отрезке
на отрезке 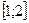
3.Проверить теорему Коши и найти с для функций: а) 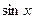 и
и 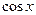 на отрезке
на отрезке 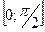 ,
,
б) х2 и 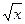 на отрезке
на отрезке  .
.
4. Разложить функцию 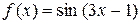 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 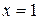 .
.
5. Найти пределы, используя разложение по формуле Тейлора
а) 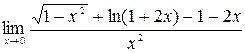 ,
,
б) 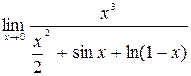 .
.
Тема 12.
Правило Лопиталя. (раскрытиенеопределенностей)
 Первое правило Лопиталя.
Первое правило Лопиталя.
Если функции  и
и 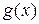 определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки  и при
и при 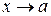
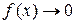 ,
, 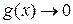 , и производные
, и производные 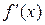 и
и 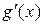 существуют в упомянутой окрестности, за исключением, быть может, самой точки и существует
существуют в упомянутой окрестности, за исключением, быть может, самой точки и существует 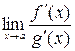 ,
,
Тогда
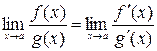 .
.
Популярное:
- A. Притяжения и отталкивания, силы отталкивания больше на малых расстояниях, чем силы притяжения. Б. Притяжения и отталкивания, силы отталкивания меньше на малых расстояниях, чем силы притяжения.
- III. Вегетативные функции НС.
- III. Предмет, метод и функции философии.
- Int mul (int x, int у); // Прототип функции mul().
- IV.1.1.2. Вычисление среднего квадратического отклонения (стандартного отклонения)
- IV.1.1.3. Вычисление коэффициента вариации
- А. Переносом стальных опилок. Б. Переносом магнита. В. Переносом проводника с током. Г. Вытягиванием его с помощью сильного электромагнита. Д. Магнитное поле переместить невозможно.
- Агрегирующие функции языка SQL
- Алгоритмы записи произвольной функции, заданной в таблице в виде с помощью элементарных функций.
- Анализ производительности с помощью анализа последовательности событий
- Антикризисный менеджмент. Функции и факторы антикризисного управления
- Антонимы. Типы антонимов. Антонимия и полисемия. Стилистические функции антонимов (антитеза, антифразис, амфитеза, астеизм, оксюморон и т.д.). Энантиосемия. Словари антонимов.

