Эпюры изгибающих моментов в однопролетных

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ............................................................................................................. 4

МЕТОД СИЛ

1. Расчет балки методом сил. Исходные данные, схемы балок......................... 5

2. Пример расчета балки методом сил............................................................... 6

3. Расчет рамы методом сил. Исходные данные, схемы рам.......................... 13

4. Пример расчета рамы методом сил.............................................................. 16

5. Контрольные вопросы по методу сил.......................................................... 29

МЕТОД ПЕРЕМЕЩЕНИЙ

6. Расчет балки методом перемещений, Исходные данные, схемы балок...... 30

7. Пример расчета балки методом перемещений............................................. 31

8. Расчет рамы методом перемещений. Исходные данные, схемы рам.......... 40

9. Пример расчета рамы методом перемещений............................................. 44

10. Контрольные вопросы по методу перемещений........................................ 59

ПРИЛОЖЕНИЯ

Эпюры изгибающих моментов в однопролетных статически неопределимых балках........................................................................................................................... 60

Использование матриц при решении систем канонических уравнений.......... 61

Список рекомендуемой методической литературы......................................... 64

ВВЕДЕНИЕ

Пособие предназначено для студентов строительных специальностей, изучающих курс строительной механики статически неопределимых систем.

Его цель помочь студентам в усвоении методов сил и перемещений и приобрести при этом необходимые навыки определения усилий и перемещений в статически неопределимых системах.

Пособие содержит задания на курсовые работы, включающие балки и рамы, которые требуется рассчитать методами сил и перемещений на действия: нагрузок, приращений температуры, заданных смещений. При этом студент должен построить эпюры внутренних силовых факторов, возникающих при каждом из воздействий, а также определить линейные и угловые перемещения заданных сечений. К каждому типу задач, включенных в задания, приводятся примеры их решения.

В приложении к пособию даны некоторые формулы и таблицы, необходимые для выполнения расчетов, элементарные сведения по матричным вычислениям и список рекомендуемой методической литературы.

Пособие может быть использовано на практических занятиях по строительной механике, при промежуточном контроле знаний студентов, а также на зачетах и экзаменах.

МЕТОД СИЛ

Расчет балки методом сил. Исходные данные, схемы балок

Для одной из заданных схем балок, изображенных на рис. 1.1–1.24 требуется:

a) изобразить расчетную схему, основную и эквивалентную системы;

b) изобразить основную систему, деформированную единичной и заданными нагрузками отдельно. Показать на этих рисунках перемещения, входящие в канонические уравнения;

c) построить эпюры внутренних силовых факторов, возникающих от нагрузки, изменения температуры и заданного смещения опор. Расчет на действие нагрузки выполнить при двух разных основных системах;

d) найти линейное и угловое перемещения сечения k при всех трех воздействиях;

e) изобразить балку, деформированную каждым из трех воздействий отдельно.

Принять: жесткость балки EI, высоту поперечного сечения h = 0, 1 L, коэффициент теплового расширения a – постоянными по длине балки; податливость упругих опор равной l = L³/EI. Другие данные принять по табл. 1.1.

Таблица 1.1

Номер варианта
F, кН
q, кН/м
М, кН× м
L, м
D, м	0, 01	0, 02	0, 03	0, 02	0, 01	0, 05	0, 04
j, рад	0, 1	0, 3	0, 2	0, 4	0, 2	0, 1	0, 3
t, °С

Пример расчета балки методом сил

2.1. Расчет на действие нагрузки

Расчетная схема балки представлена на рис. 2.1.1.

Определение усилий

Основная и эквивалентная системы изображены на рис. 2.1.2 и 2.1.3 соответственно.

Вид деформированной основной системы от единичного и силового воздействия представлен на рис. 2.1.4 и 2.1.5 соответственно, эпюры (М₁) и (М_F) – на рис. 2.1.6, 2.1.7.

В качестве неизвестных приняты силы взаимодействия (X₁) между балкой и пружиной. Они определяются из условия равенства нулю относительного перемещения точек балки и пружины, расположенных в месте их контакта. Каноническое уравнение в этом случае имеет вид:

Построение окончательных эпюр (М)^F и (Q)^F представлено на рис. 2.1.8–2.1.11.

(М)^F = (М₁)× Х₁+ (М_F).

Кинематическая проверка

Найдем угол поворота сечения А, который по условию должен быть равен нулю.

Проверка подтверждает правильность решения.

Определение перемещений сечения k

Вертикальное перемещение d _kF

Единичные загружение и эпюра (M₁)_d для определения вертикального перемещения сечения k представлены на рис. 2.1.13, 2.1.14 соответственно.

Угол поворота q _kF

Единичные загружение и эпюра (М₁)_q для определения угла поворота сечения k представлены на рис. 2.1.15, 2.1.16 соответственно.

Построение деформированной схемы рамы

Деформированная схема балки

представлена на рис. 2.1.17.

2.2. Расчет на температурное воздействие

Расчетная схема балки представлена на рис. 2.2.1.

Определение усилий

Основная и эквивалентная системы изображены на рис. 2.2.2 и 2.2.3 соответственно.

Как и в предыдущем случае (п.п. 2.1), поскольку взаимное перемещение верхней точки пружины и примыкающей к ней точки на оси балки равно нулю, получаем каноническое уравнение: (как в п.2.1).

Вид деформированной основной системы от единичного и температурного воздействия представлен на рис. 2.1.4 и 2.2.4 соответственно, эпюра (М₁) – на рис. 2.1.6.

Перемещения D₁_t, возникающие от температурного воздействия, найдем по формуле: .

Поскольку в данном случае продольных сил нет, а на эпюре (М₁) только один участок, получаем:

Подставляя соответствующие значения в каноническое уравнение, находим:

Окончательные эпюры (М)^t и (Q)^t представлено на рис. 2.2.5, 2.2.6.

(М)^t = (М₁)× Х₁.

Кинематическая проверка

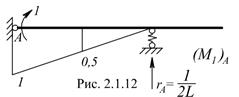
Найдем угол поворота сечения А (рис. 2.1.12), который по условию должен быть равен нулю.

Проверка подтверждает правильность решения.

Определение перемещений сечения k

Вертикальное перемещение d _kt

Единичное загружение и эпюра (M₁)_d для определения вертикального перемещения сечения k представлены на рис. 2.1.13, 2.1.14 соответственно.

Угол поворота q _kt

Единичное загружение и эпюра (M₁)_q для определения угла поворота сечения k представлены на рис. 2.1.15, 2.1.16 соответственно.

Построение деформированной схемы рамы

Деформированная схема балки

представлена на рис. 2.2.7.

2.3. Расчет на кинематическое воздействие

Расчетная схема балки представлена на рис. 2.3.1.

Определение усилий

Основная и эквивалентная системы изображены на рис. 2.3.2 и 2.3.3 соответственно.

Как и в предыдущих случаях (п.п. 2.1, 2.2), поскольку взаимное перемещение верхней точки пружины и примыкающей к ней точки на оси балки равно нулю, получаем каноническое уравнение: (как в п. 2.1).

Вид деформированной основной системы от единичного и кинематического воздействий представлен на рис. 2.1.4 и 2.3.4 соответственно, эпюра (М₁) – на рис. 2.1.6.

Перемещения D₁_D, возникающие от кинематического воздействия, найдем по формуле:

Подставляя соответствующие значения в каноническое уравнение, находим:

Окончательные эпюры (М)^D и (Q)^D представлено на рис. 2.3.5, 2.3.6.

(М)^D = (М₁)× Х₁.

Кинематическая проверка

Найдем угол поворота сечения А (рис. 2.1.12), который по условию должен быть равен нулю.

Проверка подтверждает правильность решения.

Определение перемещений сечения k

Вертикальное перемещение d _k _D

Единичные загружение и эпюра (M₁)_d для определения вертикального перемещения сечения k представлены на рис. 2.1.13, 2.1.14 соответственно.

Угол поворота q _k _D

Единичные загружение и эпюра (M₁)_q для определения угла поворота сечения k представлены на рис. 2.1.15, 2.1.16 соответственно.

Построение деформированной схемы рамы

Деформированная схема балки

представлена на рис. 2.2.7.

Расчет рамы методом сил. Исходные данные, схемы рам

Для одной из заданных схем рам, изображенных на рис. 3.1–3.24 требуется:

a) изобразить расчетную схему, основную и эквивалентную системы;

b) изобразить основную систему, деформированную единичными и заданными воздействиями. Показать на этих рисунках перемещения, входящие в канонические уравнения;

c) построить эпюры внутренних силовых факторов, возникающих от нагрузки, изменения температуры и заданного смещения опор;

d) сделать статические и кинематические проверки полученных решений;

e) найти полное линейное и угловое перемещения сечения k при всех трех воздействиях;

f) изобразить раму, деформированную каждым из трех воздействий отдельно.

Принять: изгибную жесткость стоек рамы равной EI, жесткость горизонтальных элементов и нижних частей стоек в схемах на рис. 3.16 и 3.18 равной 2 EI; высоту поперечного сечения h = 0, 1 L, коэффициент теплового расширения a – одинаковыми для всех стержней; центр тяжести поперечного сечения – в середине его высоты, j = D/2L. Другие данные принять по табл. 3.1.

Таблица 3.1

Номер варианта
F, кН
q, кН/м
L, м
D, м	0, 01	0, 02	0, 03	0, 04	0, 05	0, 02	0, 01
t_вн, °С
t_нар, °С	–30	–35	–20	–22	–28	–40	–22

4. Пример расчета рамы методом сил

Расчетная схема рамы представлена на рис. 4.1, основная и эквивалентная системы – на рис. 4.2, 4.3 соответственно.

Силы X₁ и X₂ определяются из условий отсутствия взаимного перемещения концов стержней, сходящихся в шарнире (узел 2). Эти условия записываются в форме канонических уравнений метода сил:

(4.1)

В первом уравнении написано, что перемещение по вертикали, а во втором – по горизонтали равны нулю.

Свободные члены уравнений D₁ и D₂ определяются от каждого воздействия отдельно.

4.1. Определение коэффициентов канонических уравнений

Определение d_ik

Вид деформированной основной системы от единичных воздействий представлен на рис. 4.1.1 и 4.1.2, эпюры (М₁) и (М₂) – на рис. 4.1.3, 4.1.4 соответственно.

Проверка правильности вычисления коэффициентов выполняется с помощью суммарной единичной эпюры (М_S), представленной на рис. 4.1.5.

Определение свободных членов D₁ и D ₂ от силового воздействия

Вид деформированной основной системы от силового воздействия представлен на рис. 4.1.6, эпюры (М_F) – на рис. 4.1.7.

D₁ _F и D₂ _F вычислены верно.

Определение свободных членов D₁ и D₂ от температурного воздействия

Вид деформированной основной системы от температурного воздействия представлен на рис. 4.1.8, единичные эпюры (N₁) и (N₂) – на рис. 4.1.9, 4.1.10 соответственно.

В этом случае формула для определения перемещений имеет вид:

В нашем примере получаем:

Определение свободных членов D₁ и D₂ от кинематического воздействия

Вид деформированной основной системы от кинематического воздействия представлен на рис. 4.1.11.

В этом случае формула для определения перемещений имеет вид:

В нашем примере получаем:

4.2. Определение неизвестных усилий X ₁ и X ₂

Чтобы найти эти силы необходимо решить систему уравнений (4.1), которую для краткости запишем в матричной форме:

(4.2.1)

где

Матрица B и, как следствие, матрица X зависят от вида воздействия, в то время как матрица A остается неизменной.

Для решения уравнения (4.2.1) можно пойти следующими путями.

1. Троекратное решение системы уравнений второго порядка (поскольку в нашем примере три вида нагружений).

Так, при действии нагрузки матрица B имеет вид:

и тогда уравнение (4.2.1) будет таким

Перемножив матрицы A и X, после упрощений получаем

Решив эту систему уравнений, находим:

При температурном воздействии:

уравнение (4.2.1) получает вид

Откуда

Решив систему, находим:

При расчете на смещения S и j:

Уравнение (4.2.1) получает вид

Откуда

2. Можно избежать троекратного решения системы уравнений, если воспользоваться матрицей A^–1, обратной матрице A (см. Приложение 2).

Неизвестные в этом случае находятся по формуле (2) Приложения 2:

здесь

Следовательно

Получаем .

Откуда, после перемножения матриц, находим неизвестные

3. Если использовать возможности математической системы Matlab никакие вычисления " вручную" не потребуются.

Запишем уравнение AX + B = 0 в развернутом виде, умножив его на .

Или в десятичных дробях

Обозначим и

Теперь обращаемся к Matlab и получаем X (рис. 4.2.1).

Рис. 4.2.1

Чтобы получить эту матрицу в окончательном виде вспомним, что первый ее столбец имеет множитель qL, второй – , а третий – . Заметим, кроме того, что , а .

Итак,

Незначительные расхождения в результатах объясняются погрешностями ручного счета.

4.3. Построение эпюр, проверка решения, определение перемещений от силового воздействия

Построение эпюр

Построение окончательной эпюры (М)^F, т.е. эпюры моментов, возникающих от нагрузки q, представлено на рис. 4.3.1–4.3.4.

Чтобы построить эпюру (Q)^F найдем поперечные силы в каждом стержне отдельно (рис. 4.3.5–4.3.7).

Окончательная эпюра (Q)^F представлена на рис. 4.3.8.

Когда поперечные силы найдены, из условий равновесия узлов рамы определяются продольные силы (рис. 4.3.9, 4.3.10).

Окончательная эпюра (N)^F представлена на рисунке 4.3.11.

Кинематическая проверка

Найдем угол поворота сечения на левой опоре (рис. 4.3.13), который по условию должен быть равен нулю.

Проверка равновесия рамы в целом (рис. 4.3.13)

Условия равновесия выполняются.

Можно сделать и другие статические проверки, например равновесие части рамы, равенства нулю изгибающего момента в шарнире (узел 2) и т.п.

Определение перемещений сечения k

Линейное перемещение d_kF

Единичная эпюра (M₁)_d для определения линейного перемещения сечения k представлена на рис. 4.3.14.

Поскольку принято, что длины стержней при силовом нагружении не изменяются, то горизонтальное перемещение сечения k является его полным перемещением.

Угол поворота q_kF

Единичная эпюра (M₁)_q для определения угла поворота сечения k представлена на рис. 4.3.15.

Построение деформированной схемы рамы

Деформированная схема рамы представлена на рис. 4.3.16.

4.4. Построение эпюр, проверка решения, определение перемещений от температурного воздействия

Построение эпюр

Построение окончательной эпюры (М)^t представлено на рис. 4.4.1–4.4.3.

Правила построения эпюр (Q) и (N) подробно рассмотрены в разделе 4.3. Пользуясь этими правилами строим эпюры (Q)^t и (N)^t – рис. 4.4.4, 4.4.5.

Кинематическая проверка

Найдем угол поворота сечения на левой опоре (рис. 4.3.13), который по условию должен быть равен нулю. Дополнительная эпюра , необходимая для нахождения угла поворота, представлена на рис. 4.4.6.

Проверка подтверждает правильность решения.

Проверка равновесия рамы в целом (рис. 4.4.7)

Условия равновесия выполняются.

Определение перемещений сечения k

Линейное перемещение d_kt

Единичные эпюры (M₁)_d и (N₁)_d для определения линейного перемещения сечения k представлены на рис. 4.3.14 и 4.4.8 соответственно.

Угол поворота q _kt

Единичная эпюра (M₁)_q для определения угла поворота сечения k представлена на рис. 4.3.15.

Построение деформированной схемы рамы

Деформированная схема рамы представлена на рис. 4.4.9.

4.5. Построение эпюр, проверка решения, определение перемещений от кинематического воздействия

Построение эпюр

Построение окончательной эпюры (М)^D представлено на рис. 4.5.1–4.5.3.

Эпюры (Q)^D и (N)^D представлены на рис. 4.5.4, 4.5.5.

Кинематическая проверка

Найдем угол поворота сечения на левой опоре (рис. 4.3.13), который по условию должен быть равен нулю.

Проверка подтверждает правильность решения.

Проверка равновесия рамы в целом (рис. 4.5.6)

Очевидно, что

Условия равновесия выполняются.

Определение перемещений сечения k

Линейное перемещение d_k_D

Единичная эпюра (M₁)_d для определения линейного перемещения сечения k представлена на рис. 4.3.14.

Перемещения определяются по формуле

– по условию.

м.

Угол поворота q_k_D

Единичная эпюра (M₁)_q для определения угла поворота сечения k представлена на рис. 4.3.15.

рад.

Построение деформированной схемы рамы

Деформированная схема рамы представлена на рис. 4.5.7

3

5. Контрольные вопросы по методу сил

1. Какая система называется статически неопределимой? Как найти степень статической неопределимости?

2. Что принимается за неизвестные метода сил? Что такое основная и эквивалентная системы метода сил?

3. Как вы понимаете идею метода сил?

4. Как с помощью суммарной единичной эпюры проверить правильность коэффициентов канонических уравнений?

5. Как определяются свободные члены канонических уравнений при расчете на температурные воздействия, на заданные смещения?

6. Каков физический смысл и особенности канонических уравнений метода сил?

7. Каков физический смысл коэффициентов при неизвестных и свободных членов в канонических уравнениях?

МЕТОД ПЕРЕМЕЩЕНИЙ

Расчет балки методом перемещений, Исходные данные, схемы балок

Для одной из заданных схем балок, изображенных на рис. 6.1–6.24 требуется:

a) изобразить расчетную схему, основную систему и эквивалентную системы;

b) изобразить основную систему, деформированную единичным и заданными воздействиями. Показать на этих рисунках величины, входящие в канонические уравнения;

d) найти линейное и угловое перемещения сечения k при всех трех воздействиях;

e) изобразить балку, деформированную каждым из трех воздействий отдельно.

Принять: жесткость балки EI, высоту поперечного сечения h = 0, 1 L, коэффициент теплового расширения α – постоянными по длине балки; жесткость податливых связей равной k = EI / L ³(податливость – l = L³/EI ), φ = ∆ /L. Другие данные принять по табл. 6.1.

Таблица 6.1

Номер варианта
F, кН
q, кН/м
М, кН× м
L, м
D, м	0, 01	0, 02	0, 03	0, 04	0, 01	0, 02	0, 03
t, °С

7. Пример расчета балки методом перемещений

Расчетная схема балки представлена на рис. 7.1, основная система – на рис. 7.2.

В качестве неизвестных здесь приняты: Z₁– угол поворота узла B и Z₂ – вертикальное перемещение этого узла. Они определяются из условий равенства нулю реакций в дополнительных связях 1 и 2, которые записываются в форме канонических уравнений метода перемещений:

(7.1)

В первом уравнении написано, что реакция (момент) в первой связи равна 0, во втором – реакция (усилие) во второй связи равна 0.

7.1. Определение коэффициентов канонических уравнений

Изгибающие моменты и поперечные силы, возникающие в стержнях основной системы, определяются по таблицам Приложения 1.

Определение r_ik

Схема деформирования и эпюра моментов от единичного смещения первой связи (поворот узла на Z ₁ = 1) представлены на рис. 7.1.1 и 7.1.2 соответственно. Схемы определения реакций во введенных связях – на рис. 7.1.3, 7.1.4.

Определение r₁₁Определение r₂₁

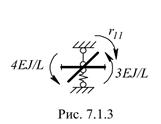
Схема деформирования и эпюра моментов от единичного смещения второй связи (линейное перемещение на Z ₂ = 1) представлены на рис. 7.1.5 и 7.1.6 соответственно. Схемы определения реакций во введенных связях – на рис. 7.1.7, 7.1.8.

Определение r₁₂Определение r₂₂

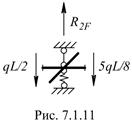
Определение свободных членов R₁ и R₂ от силового воздействия

Эпюра моментов в ОС от силового воздействия представлена на рис. 7.1.9. Схемы определения реакций во введенных связях – на рис. 7.1.10, 7.1.11.

Определение R₁_F Определение R₂_F

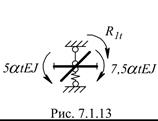
Определение свободных членов R₁ и R₂ от температурного воздействия

Эпюра моментов в ОС от температурного воздействия представлена на рис. 7.1.12. Схемы определения реакций во введенных связях – на рис. 7.1.13, 7.1.14.

Определение R₁_t Определение R₂_t

Определение свободных членов R₁ и R₂ от кинематического воздействия

Эпюра моментов в ОС от кинематического воздействия представлена на рис. 7.1.15. Схемы определения реакций во введенных связях – на рис. 7.1.16, 7.1.17.

Определение R₁_D Определение R₂_D