ИЗУЧЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
Цель работы: рассматриваются понятия тензора инерции, эллипсоида инерции при вращении твердого тела.
Теория
Тензор инерции
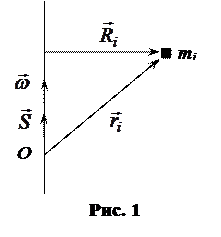 При описании вращательного движения твердого тела часто появляется необходимость знать его движение около точки закрепления. Важнейшим понятием при этом является тензор инерции. Для упрощения расчетов воспользуемся представлением о теле как совокупности материальных точек с массами
При описании вращательного движения твердого тела часто появляется необходимость знать его движение около точки закрепления. Важнейшим понятием при этом является тензор инерции. Для упрощения расчетов воспользуемся представлением о теле как совокупности материальных точек с массами 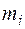 .
.
Закрепим тело в точке 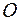 . Радиус-вектор точки с массой
. Радиус-вектор точки с массой 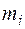 относительно
относительно 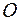 обозначим
обозначим 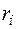 (см. рис. 1). Пусть
(см. рис. 1). Пусть 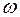 - мгновенная угловая скорость тела. Тогда скорость
- мгновенная угловая скорость тела. Тогда скорость 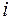 - й точки тела
- й точки тела 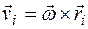 . Поэтому момент импульса
. Поэтому момент импульса 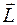 всего тела относительно точки
всего тела относительно точки 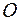 равен:
равен:
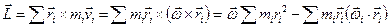
. (1)
где использована формула разложения двойного векторного произведения 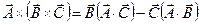 .
.
Векторное равенство (1) можно написать в виде трех проекций на оси координат:
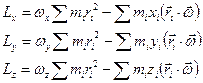 . (2)
. (2)
Учитывая, что 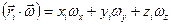 , вместо (2) имеем
, вместо (2) имеем
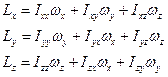 . (3)
. (3)
где:
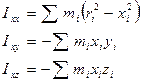 . (3а)
. (3а)
аналогично выражаются другие величины 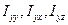 и т.д. Поэтому из 9 величин
и т.д. Поэтому из 9 величин 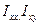 , различны лишь 6. Величины
, различны лишь 6. Величины 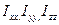 называются осевыми моментами инерции, а
называются осевыми моментами инерции, а 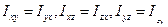 называются центробежными моментами инерции. Таким образом, момент импульса тела весьма сложно зависит от распределения масс в теле, и его направление не всегда совпадает, с угловой скоростью вращения тела. Совокупность величин
называются центробежными моментами инерции. Таким образом, момент импульса тела весьма сложно зависит от распределения масс в теле, и его направление не всегда совпадает, с угловой скоростью вращения тела. Совокупность величин
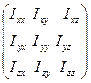 . (4)
. (4)
называется тензором инерции. Величины 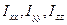 являются диагональными элементами тензора, а остальные – недиагональными. Если величины, расположенные симметрично относительно диагонали, равны, то такой тензор называется симметричным.
являются диагональными элементами тензора, а остальные – недиагональными. Если величины, расположенные симметрично относительно диагонали, равны, то такой тензор называется симметричным.
Главные оси тензора инерции
Предположим, что все недиагональные элементы тензора равны 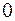 , а отличными от нуля являются лишь диагональные, т.е. тензор имеет следующий вид:
, а отличными от нуля являются лишь диагональные, т.е. тензор имеет следующий вид:
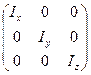 .
.
При такой ситуации говорят, что оси тензора, совпадающие с осями координат, являются главными осями инерции, а величины 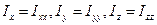 называют главными моментами инерции. О тензоре в этом случае говорят, что он приведен к диагональному виду. Таким образом, если оси системы координат направлены вдоль главных осей инерции тела, то центробежные моменты инерции отсутствуют. Процесс нахождения главных осей сводится к математической процедуре диагонализации тензора. Здесь нет необходимости ее рассматривать.
называют главными моментами инерции. О тензоре в этом случае говорят, что он приведен к диагональному виду. Таким образом, если оси системы координат направлены вдоль главных осей инерции тела, то центробежные моменты инерции отсутствуют. Процесс нахождения главных осей сводится к математической процедуре диагонализации тензора. Здесь нет необходимости ее рассматривать.
Отметим лишь результат: через любую точку твердого тела можно провести три взаимно-перпендикулярные главные оси. Главные моменты инерции 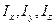 будут различны для различных точек тела. Если главные оси проведены через центр масс тела, они называются центральными главными осями. Таким образом, не имеет смысла говорить о главных моментах инерции тела, не указав точки тела, через которую проведены главные оси.
будут различны для различных точек тела. Если главные оси проведены через центр масс тела, они называются центральными главными осями. Таким образом, не имеет смысла говорить о главных моментах инерции тела, не указав точки тела, через которую проведены главные оси.
 При переходе от одной точки тела к другой главные оси, вообще говоря, меняют свое направление, а главные моменты свое значение.
При переходе от одной точки тела к другой главные оси, вообще говоря, меняют свое направление, а главные моменты свое значение.
Например, не имеет смысла начертить в теле ось и сказать, что она главная. Лишь когда речь идет о центральных главных осях и центральных главных моментах инерции, нет необходимости указать точку тела, к которой они относятся, потому что по определению известно, что это точка центра масс тела. Особенное значение имеет осевой момент инерции (рис.2), равный
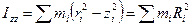 . (5)
. (5)
где 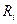 – расстояние точки
– расстояние точки 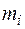 от оси, поскольку во многих случаях он позволяет полностью описать динамику вращения твердого тела. Его также называют моментом инерции тела относительно оси.
от оси, поскольку во многих случаях он позволяет полностью описать динамику вращения твердого тела. Его также называют моментом инерции тела относительно оси.
Нахождение главных осей
 Главные оси во многих случаях могут быть найдены без громоздких математических расчетов, которые надо провести для диагонализации тензора инерции. Для этого иногда бывает достаточно воспользоваться простыми соображениями симметрии. Пусть имеется плоская пластинка бесконечно малой толщины. Точка, через которую проходят главные оси, лежит на пластинке. Направим ось
Главные оси во многих случаях могут быть найдены без громоздких математических расчетов, которые надо провести для диагонализации тензора инерции. Для этого иногда бывает достаточно воспользоваться простыми соображениями симметрии. Пусть имеется плоская пластинка бесконечно малой толщины. Точка, через которую проходят главные оси, лежит на пластинке. Направим ось 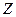 перпендикулярно ей. Очевидно, что координаты
перпендикулярно ей. Очевидно, что координаты 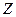 всех точек пластинки равны нулю, т.е. все
всех точек пластинки равны нулю, т.е. все 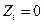 . В этом случае из формулы (3) имеем
. В этом случае из формулы (3) имеем 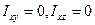 . Следовательно, любая ось, перпендикулярная этой пластинке, будет главной. Две другие главные оси расположены в плоскости пластинки взаимно перпендикулярно друг другу. Их направление зависит от формы пластинки.
. Следовательно, любая ось, перпендикулярная этой пластинке, будет главной. Две другие главные оси расположены в плоскости пластинки взаимно перпендикулярно друг другу. Их направление зависит от формы пластинки.
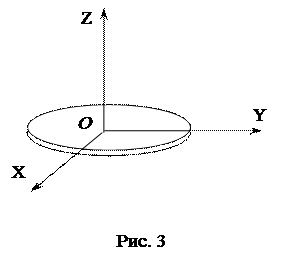
Рассмотрим случай круглой пластинки (рис.3) конечной толщины. Точка 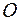 , лежащая в средней плоскости пластинки, есть точка, относительно которой надо найти главные оси. Очевидно, что одна главная ось направлена перпендикулярно плоскости пластинки. Утверждается, что другой главной осью является ось, лежащая в средней плоскости и проходящая через эту точку и центр диска. Эта ось на рис.3 взята за ось
, лежащая в средней плоскости пластинки, есть точка, относительно которой надо найти главные оси. Очевидно, что одна главная ось направлена перпендикулярно плоскости пластинки. Утверждается, что другой главной осью является ось, лежащая в средней плоскости и проходящая через эту точку и центр диска. Эта ось на рис.3 взята за ось 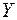 . Убедимся в этом. Имеем:
. Убедимся в этом. Имеем:
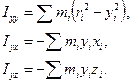
Видно, что 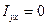 и
и 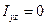 из-за симметрии пластинки относительно плоскостей
из-за симметрии пластинки относительно плоскостей 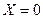 и
и 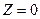 . Таким образом, выбранная ось действительно является главной. Третья главная ось однозначно определяется двумя найденными, будучи перпендикулярной им обеим. Проверим, что ось
. Таким образом, выбранная ось действительно является главной. Третья главная ось однозначно определяется двумя найденными, будучи перпендикулярной им обеим. Проверим, что ось 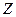 действительно является главной. Имеем:
действительно является главной. Имеем:
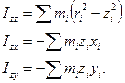 (7)
(7)
Равенства 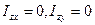 обусловливаются симметрией пластинки относительно плоскости
обусловливаются симметрией пластинки относительно плоскости 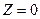 .
.
Если круглая пластинка имеет значительную толщину, то она называется круглым цилиндром. Все изложенные о главных осях пластинки соображения остаются, конечно, справедливыми и для цилиндра.
Популярное:


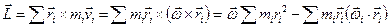 . (1)
. (1)