
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Если двузначное число разделить на сумму его цифр, то получится в частном 4 и в остатке 3. Если это число разделить на произведение его цифр, то получится в частном 3 и в остатке 5.
Найдите это двузначное число. Ответ: 23 Пример 11 Решить уравнения: 1) 2002х2-2001х-1=0; 57х2-101х-26=0. Ответ: 1) {1; - Пример 12 При каких значениях параметра «а» число Ответ: а=-1; а=1. ГЛАВА 2. Модуль вещественного числа. Решение уравнений и неравенств со знаком модуля. |f(x)|= Простейшие уравнения со знаком модуля. 1. |f(x)|=a® 2. | f(x) | =g(x) « 3. |f(x)|=|g(x)|« частный случай: |х-а|=|х-в| « х= 4. |f(x)|+|g(x)|=0 « Пример 1 Решить уравнения: 1) |5-3х|=2; 2) |х2-13х+40|=0; 3) |4-х2|=-2. Решение: 1) |5-3х|=2« Ответ: {1; 2) | х2-13х+40 | =0 « х2-13х+40=0 « Ответ: {5; 8} 3) | 4-х2 | =-2 « Пример 2 Решить уравнения: 1) |х2-5х-6|=2х-12; 2) |х2-3х-10|=2х+14; 3) |х2-25|=-30-6х; 4) |х2-7х+18|=2х-2; 5) |х2+5х+13|=-2х+1. Решения: 1) |х2-5х-6|=2х-12 О.Д.З. 2х-12³ 0« х³ 6 Заметим, что х2-5х-6³ 0 при х³ 6, т.к. х2-5х-6=(х-6)*(х+1)
|х2-5х-6|= х2-5х-6® х2-5х-6=2х-12 « х2-7х+6=0 « Ответ: {6} 2) | х2-3х-10 | =2х+14 «
Ответ: {-5; 8} 3) |х2-25|=-30-6х О.Д.З. -30-6х³ 0« х≤ -5
|х2-25|= х2-25 ® х2-25=-30-6х « х2+6х+5=0 « 4) |х2-7х+18|=2х-2 «
Ответ: {4; 5} 5) | х2+5х+13 | =-2х+1 « Ответ: {3; 4} Пример 3 Решить уравнения: 1) |2х2+3х+5|=|2х2+3х-3|; 2) |х3+х-1|=|х3+х+5|; 3) |х2-4х+8|=|х2-14|; 4)|х3-27|+|х2-4х+3|=0; 5) | Решения: 1) | 2х2+3х+5 | = | 2х2+3х-3 |; пусть 2х2+3х=t ®| t+5 | = | t-3 |« t= 2х2+3х=-1« Ответ: {-0, 5; -1} 2) | х3+х-1 | = | х3+х+5 |; пусть х3+х=t ®| t-1 | = | t+5 |« t= х3+х=-2« х3+х+2=0 « (x3+1)+(x+1)=0« (x+1)(x2-x+2)=0 « x=-1 (x2-x+2 Ответ: {-1} 3) | х2-4х+8 | = | х2-14 |« « Ответ: {-1; 3; 5, 5} 4)|х3-27|+|х2-4х+3|=0 « Ответ: {3} 5) | Ответ: {2} Пример 4 Решить уравнение: |х-3|-|2х+1|=х-4 Решение: |х-3|-|2х+1|=х-4
Пример 5 Решить уравнения (самостоятельно) 1) |7+12х|=4; 2) |х4-27х|=0; 3) |5-х3+х|=-1 Ответ: 1){- Пример 6 Решить уравнения (самостоятельно) 1) |х2-7х+6|=х-6; 2) |х2-10х+2|=-5х+54; 3) |49-х2|=-3х-21; 4) |х2-4х+3|=2х+10; 5) |х2+9х+8|=4х+2. Ответ: 1){6}; 2) {7; 8; Пример 7 Решить уравнения (самостоятельно) 1) |4х2-6х-1|=|4х2-6х-7|; 2) |2х3-х|=|2х3-х-2|; 3)|х2+2х+10|=|х2-50|; 4)|х3+125|+|х2+4х-5|=0; 5) | Ответ: 1){-0, 5; 2}; 2) {1}; 3) {-30; -5; 4}; 4) {-5}; 5){-1} Пример 8 Решить уравнение (самостоятельно) |3х+1|-|х+2|=4-2х. Ответ: { Простейшие неравенства со знаком модуля. 1.
2.
Ответ: xÎ [x0-a; x0+a] 3.
Ответ: xÎ ( 4.
Ответ: xÎ 5. |f(x)|≤ a (a> 0) « 6. |f(x)|³ a (a> 0) « 7. 8. 9. 10. |f(x)|³ g(x) « 11. |f(x)|³ |g(x)| « 12. |f(x)|≤ |g(x)| « Пример 1 Решить следующие неравенства: 1) |3х-15|> 10; 2) |7х+12|≤ 5; 3) |7-5х|³ 7; 4) |4-3х|≤ 4; 5)
1)
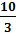
Ответ: хÎ (- 2)
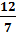 |≤ |≤ 
Ответ: хÎ [- 3)
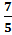 |³ |³ 
Ответ: хÎ 4)
Ответ: хÎ [0; 8/3] 5) Ответ: хÎ
Ответ: хÎ ( 6) Ответ: 8) Ответ: хÎ ( Пример 2 Решить следующие неравенства: (самостоятельно) 1) |5х-2|³ 10; 2) |4-3х|< 12; 3) |2х+10|> 1; 4) |10х+1|≤ 20; 5) 6) Ответы: 1) 4) [-2, 1; 1, 9]; 5) ( 7) Пример 3 Решить следующие неравенства: 1) |х2+25|≤ 10х; 2) |х2+6х+10|³ 5; 3) |х+8|≤ х2+6; 4) |х2-4|³ 2х-5; 5) |х2-5х|< 3х-7; 6) |х2-6|≤ |х2+4х|; 7) |2х+5|> |х2-4х-2|; 8) |х2+5х+9|≤ |х2-7х-4| Решения: 1) | х2+25 | ≤ 10х( т.к. х2+25> 0, то | х2+25 | =х2+25) « х2+25≤ 10х « « х2-10х+25≤ 0 « (х-5)2≤ 0 « х=5 Ответ: {5} 2) | х2+6х+10 |³ 5 (т.к. х2+6х+10> 0 /дискриминант отрицательный/, то |х2+6х+10|=х2+6х+10 ) « х2+6х+10³ 5 « х2+6х+5³ 0 « (х+5)*(х+1)³ 0
Ответ: хÎ 3) | х+8 | ≤ х2+6 (x2+6> 0) «
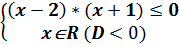
Ответ: хÎ [-1; 2] 4) | х2-4 |³ 2х-5 « « Ответ: хÎ 5) | х2-5х |< 3х-7 « «
Ответ: хÎ (1+ 6) | х2-6 | ≤ | х2+4х |« 6) (х2-6)2≤ (х2+4х)2 « (х2-6)2-(х2+4х)2≤ 0 «
Ответ: xÎ [-3; -3/2] 7) | 2х+5 | > | х2-4х-2 |« (2х+5)2> (х2-4х-2)2 « (2х+5)2-(х2-4х-2)2> 0 «
Ответ: хÎ (1; 7) 8) |х2+5х+9|≤ |х2-7х-4| Заметим. что х2+5х+9> 0 т.к. D< 0 ® | х2+5х+9 | =х2+5х+9®|x2-7x-4|³ х2+5х+9 « Ответ: хÎ (- Пример 4 Решить следующие неравенства (самостоятельно): 1) |х2+81|³ -18х; 2) |х2-8х+14|≤ 2; 3) |2х+1|³ х2+2; 4) |х2-10х+14|< 2х+3; 5) |4х-13|³ х2-9; 6) |х2-2х+2|³ |6-х2|; 7) |х2-2х-3|> 2|х-3|; 8) |х2-7х+2|≤ |х2-7х+10|. Ответы: 1) (-∞; +∞ ); 2) [2; 6]; 3) {1}; 4) (1; 11); 5)[-2- 6) (- Пример 5 Решить следующие неравенства: 1) |х-1|-|2х+5|³ 3х-4; 2) |2х+1|+|4-2х|≤ 6х+1. Решения: 1)
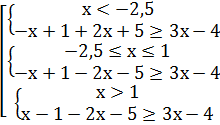 « « 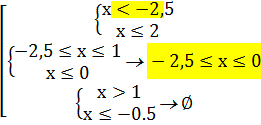
2)
Ответ: хÎ [2/3; +∞ ) Пример 6 Решить следующие неравенства (самостоятельно) 1) |3х+1|-|2х-3|≤ х+5; 2) |4х-8|+|4х+12|³ 5-4х. Ответы: 1)[ -4, 5; +∞ ); 2) (-∞; +∞ ). Пример 7 Решить следующие неравенства: 1) Решение: 1) Ответ: хÎ (-1/3; 1/3) 2) | Ответ: хÎ [-5/3; -1) 3) |
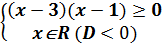
Ответ: xÎ (- 4) Ответ: хÎ (-∞; -3) Пример 8 Решить следующие неравенства (самостоятельно) 1) Ответ: 1) хÎ 3) xÎ Пример 9 Решить системы неравенств: 1) Решение: 1)
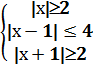
Ответ: xÎ [2; 5] 2)
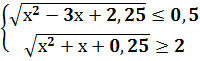 « «
« Ответ: xÎ [1, 5; 2] Пример 10 Решить системы неравенств (самостоятельно): 1) Ответ: 1) xÎ [2; 4] ГЛАВА 3. Элементы теории множеств. §1Основные понятия. Напомним, что универсальное множество, которое содержит в себе все другие множества, обозначается буквой W. Пустое множество обозначается
А A A\B (разность множеств) « {x| (xÎ A)Ù (x
При работе с множествами будем использовать следующие свойства основных операций над множествами.
Примечание: формулы 6 и 7 называют формулами де Моргана
§2 Решение примеров. Пример 1. Дано: АÌ ВÌ СÌ D Упростить: а) ( b) ( c) Решение:
а) ( Ответ: B b) ( Заметим, что Ответ: c) Ответ: Пример 2 Дано: AÌ B; CÌ D; Упростить: a) b) c) d) Решение:
a) Ответ: в) Ответ: С с) Ответ: d) Ответ: D Пример 3 Упростить:
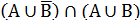
Решение:
Ответ: А Пример 4 Упростить:
Решение:
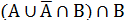 =( =( 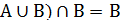
Ответ: В Пример 5 Упростить:
Решение:
Ответ: Пример 6 Упростить:
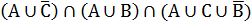
Решение:
Ответ: А Пример 7 Дано: A={xÎ R| |x-2|³ 2}; B={xÎ R| |x|≤ 4}; C={xÎ R| |x+1|≤ 5} Найти: a) Решение:
А=
B=[-4; 4]
C=[-6; 4] Ответ: a) b) c) Пример 8 Дано: A={xÎ R| Найти: а) Решение: A={xÎ R|
A=[-0, 5; 1, 5]
B={xÎ R|
B= Ответ: a) ; c)A\B=[-0, 5; 0] Пример 9 (самостоятельно) Дано: Упростить: a) b) c) ( d) e) Ответ: a) A; b) D; c) Пример 10. (самостоятельно) Дано: AÌ BÌ C; C∩ D=∅ Упростить: a) (A∪ B∪ C)∩ b) (A∩ C)∪ B∩ D c) ( Ответ: a) C; b)C; c) B∪ D. Пример 11 (самостоятельно) Упростить: (А∪ (А∩ В))∩ (А∩ В). Ответ: А∩ В Пример 12 (самостоятельно) Упростить: (А∩ В)∪ (А∩ Ответ: А Пример 13 (самостоятельно) Упростить: (А∩ Ответ: А Пример 14 (самостоятельно) Упростить: А∩ (А∪ А∩ В)∪ В∩ ( Ответ: В Пример 15 (самостоятельно) Дано: A={x∈ R| |x+0, 5|≤ 2, 5}; B={xÎ R| |x-0, 5|³ 0, 5}; C={xÎ R| |x+0, 4|≤ 2, 6} Найти: a) A∪ B∪ C; b)A∩ B∩ C; c)(A∪ C)∩ B Ответ: a) R; b)[-3; 1]∪ {2}; c) [-3; 1]∪ [2; 2, 2] Пример 16 (самостоятельно) Дано: A={xÎ R| B={xÎ R| Найти: a) A∪ B; b)A∩ B; c)A\B. Ответ: a) (-∞; -1, 6]∪ [11/3; +∞ ); b) [-2, 4; -7/3]; c) (-7/3; 1, 6] Пример 17 Дано: A={xÎ R| |4x2+1|≤ 4x}; B={xÎ R| |x+3|-|2x+1|≤ x+4} Найти: a)C=A∪ B; b)D=A∩ B; c)E= Решение: |4x2+1|≤ 4x « 4x2+1≤ 4x « 4x2+1-4x≤ 0 « (2х-1)2≤ 0«
|x+3|-|2x+1|≤ x+4
B=R Ответ: a)C=R; b)D=A={0, 5}; c)E=∅ Пример 18 Дано: A={xÎ R| |6x2-14x+18, 8|-x2-9=0}; B={xÎ R| Найти: А∪ В. Решение: |6x2-14x+18, 8|-x2-9=0 « « A={1, 4}
B=(-∞; -0, 2]∪ [0, 2; √ 3/2)∪ (√ 3/2; +∞ ) |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 756; Нарушение авторского права страницы