
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Напомним, что графиком этой функции является гипербола.
Ниже приведены схемы графиков.
Пример 1. Построить график функции и провести исследование. у= Решение: Сначала выделим целую часть: у=2- Исследование: 1. Область определения функции: D(f)=(-∞; -3)∪ (-3; +∞ ) Прямая х=-3- вертикальная асимптота 2. Множество значений функции: E(f)=(-∞; 2)∪ (2; +∞ ). Прямая У=2- горизонтальная асимптота. Точка (-3; 2)- центр симметрии.
т 4. f(x)≠ 5.Функция возрастает, т.к. к=-7< 0. Экстремумов нет. Схема данного графика имеет вид:
Пример 2. Построить график функции и провести исследование. у = Решение: Сначала построим график данной функции, используя метод преобразования графиков в следующем порядке: Построим график функции у= На рисунке показана схема полученного графика.
Исследование: 1. Область определения функции: D(f)=(-∞; -1)∪ (-1; 1)∪ (1; +∞ ) Прямые х=-1 и х=1 - вертикальные асимптоты. 2. Множество значений функции: E(f)=(-∞; -2]∪ (3; +∞ ) прямая у=3 -горизонтальная асимптота 3)
4) Чётность - нечётность. f(-x)=f(x)-®функция чётная (график симметричен относительно оси ординат)) 5) Экстремумы: max y(0)=-2. Пример 3. Построить график функции и провести исследование. у=| Решение: у=| Сначала построим график данной функции, используя метод преобразования графиков в следующем порядке: 1) у= 2) у=1- 3) у=1- 4) у= | 1- На рисунке показана схема полученного графика. Далее, используя график, можно продолжить исследование
Проведём исследование этой функции. 1).Область определения функции: D(f)=(-∞; +∞ ) 2) Множество значений функции: E(f)=[0; 2, 5] Прямая у=1 - горизонтальная асимптота. 3).Множество корней: у=0 «| х | -5=0 «| х | =5 «
4) Чётность - нечётность. f(-x)=f(x)-®функция чётная (график симметричен относительно оси ординат)) 5) Экстремумы: max y(0)=2, 5; min y(±5)=0
Пример 4 (самостоятельно). Построить график функции и провести исследование. у= Пример 5 (самостоятельно). Построить график функции и провести исследование. у= Пример 6 (самостоятельно). Построить график функции и провести исследование. у=| Степенная функция. Функция вида: у=х𝛂 , 𝛂 Î Q Называется степенной функцией Примечание:. При любом значении «𝛂 » график степенной функции проходит через точку (1; 1) Исследуем степенную функцию для различных значений «𝛂 ».
Общий случай.
Пусть х³ 0.
Примечание: При х< 0 нужно провести дополнительное исследование. Возможны варианты: а) Если D(f)=[0; +∞ ), то при х< 0 нет продолжения. б) Если D(f)=R, то возможно чётное или нечётное продолжение Пример 1. Построить схемы графиков и провести исследование данных функций: 1) у= 2) у= 3) у= 4) у= Решение:
Если при х> 0®
Примечание: При х< 0 нужно провести дополнительное исследование. Возможны варианты: а) Если D(f)=(0; +∞ ), то при х< 0 нет продолжения. б) Если D(f)=R\{0}, то возможно чётное или нечётное продолжение Пример 2. Построить схемы графиков и провести исследование данных функций: 1)Y= Решение:
Пример 3. Построить схему графика и провести исследование данной функции: у= Решение: Сначала построим схему графика у= Заметим, что. функция у= Затем сдвигаем ось абсцисс на 1 вверх.
Исследование этой функции проводим с использованием построенного графика. 1) D(f)=R 2) E(f)=[-1; +∞ ) 3) y=0«|x|=1« 4) f(-x)=f(x)® функция чётная 5) на интервале (-∞; 0) функция убывает на интервале (0; +∞ ) функция возрастает. 6) min y(0)=-1 Пример 4. Построить схему графика и провести исследование данной функции: у= Решение: Сначала построим схему графика у=
1) D(f)=(0; +∞ ); прямая х=0 - вертикальная асимптота 2) E(f)=(2; +∞ ); прямая у=2 - горизонтальная асимптота Корней нет Функция общего вида 5) на всей области определения функция убывает Экстремумов нет Пример 5. Построить схему графика и провести исследование данной функции: у= Решение: Сначала построим схему графика у= у=
1) D(f)=R 2) E(f)=[-2; +∞ ) 3) y=0« 4) f(-x)=f(x)®функция чётная 5) на интервале (-∞; 0) функция убывает, на интервале (0; +∞ ) функция возрастает 6) min y(0)=-2
Пример 6. Построить схему графика и провести исследование данной функции: у= Решение:
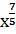 ( (  > 1® ) > 1® )
у=
(исследование проведите самостоятельно) Пример 7 (самостоятельно). Построить схему графика и провести исследование данной функции: у= Пример 8 Самостоятельно). Построить схему графика и провести исследование данной функции: у= Пример 9 (самостоятельно). Построить схему графика и провести исследование данной функции: у= Пример 10 (самостоятельно) Построить схему графика и провести исследование данной функции: у= Квадратичная функция. Функция вида: у=ax2+bx+c |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 905; Нарушение авторского права страницы