
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Построить график и провести исследование по предложенной выше схеме.
у=2|х+1|-3 · к=2> 0® Ú · ось симметрии х=-1 · вершина ломаной (-1; -3) · корни: у=0 « 2 | х+1 | -3=0«2|х+1|=3«|х+1|=
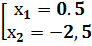
·
·
Пример 2
y=4-|2x+1| « y=4-2|x+0, 5| · k=-2< 0 ®Ù ·
·
·
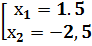
· у(0)=3 · max y(-0, 5)=4
В точках А и В имеем узлы ломаной. у(а)=|а-b|=𝛂 ®A(a; 𝛂 ) v(b)=|b-a|=𝛂 ®B(b; 𝛂 ) Дополнительные точки: y(a-1)=1+|a-1-b|=𝛃; C(a-1; 𝛃 ) y(b+1)=|b+1-a|+1=1+|a-1-b|=𝛃; D(b+1; 𝛃 )
Если раскрыть знак модуля, то получим следующее аналитическое задание функции: у = 4. «ступенька» у=|x-a|-|x-b| Можно провести исследования, аналогичные предыдущей функции и получим следующие характерные графики:
b> a
Пример 3 Решить уравнение.
Решение: О.Д.З.: х³ 4
Пусть t= Покажем графическое решение этого уравнения.
Строим графики этих функций на одном чертеже и находим решение системы
Решение системы: 0≤ t≤ 2 «0≤ Ответ: хÎ [4; 8] Пример 4. Решить уравнение.
Решение:
Пусть Покажем графическое решение этого уравнения.
Решение системы: t³ 5« Ответ: хÎ [23; +∞ ) 5.y=||x-a|-b| (W) Ось симметрии х=а.
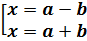 ( корни функции) ( корни функции)
Пример 5. Сколько решений имеет уравнение в зависимости от параметра «а» ||х+1|-2|=х+а. Решение: Покажем графическое решение примера.
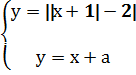
Построение графиков и исследование функций со знаком модуля. Пример 1 Исследовать и построить график функции: у= Решение: y= 1) D(f)=(-∞; 0)∪ (0; +∞ ) 2) E(f)={-1; 1} Корней нет 4) чётность-нечётность: f(x)= 5) наибольшее значение: у=1; наименьшее значение у=-1®extr нет Функция кусочно- постоянная
Пример 2 Исследовать и построить график функции: у= Решение: y= 1) D(f)=(-∞; 1)∪ (1; +∞ ) 2) E(f)={0; 2} 3) множество корней: (-∞; 1) 4) чётность-нечётность: f(x)≠ 5) наибольшее значение: у=2; наименьшее значение у=0®extr нет 6)
Пример 3 Исследовать и построить график функции: y= Решение: у= 1)D(f)=(-∞; 0, 5)∪ (0, 5; +∞ ) В точке х=0, 5 функция имеет разрыв.Исследуем поведение функции вблизи точки разрыва.
Построим график этой функции, а затем продолжим исследование. у=х+1; у(1)=2; у(0, 5)=1, 5®точка разрыва справа. у=х-3; у(0)=-3; у(0, 5)=-2, 5®точка разрыва слева
2) E(f)=(-∞; -2, 5)∪ (1, 5; +∞ ) Корней нет 4) чётность-нечётность: f(x)≠ 5) функция строго возрастает® extr нет Пример 4 (самостоятельно) Исследовать и построить график функции: у= Пример 5 (самостоятельно) Исследовать и построить график функции: у=5- Пример 6 (самостоятельно) Исследовать и построить график функции: у=х+1- Пример 7 Исследовать и построить график функции: у= Решение: у= 1) D(f)=(-∞; -1)∪ (-1; +∞ ) 2) E(f)={-2.8; 2} Множество корней: корней нет 4) чётность-нечётность: f(x)≠ 5) наибольшее значение: у=2; наименьшее значение у=-2, 8®extr нет Функция кусочно- постоянная
Пример 8 Исследовать и построить график функции: у= Решение:
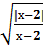 -3 ® у=0 при х> 2 -3 ® у=0 при х> 2
1)D(f)=(2; +∞ )
Функция общего вида 5)постоянная: у=0 Пример 9 Исследовать и построить график функции: у= Решение:
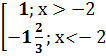
1)
2)
 ; 1} ; 1}
Множество корней: корней нет 4) чётность-нечётность: f(x)≠ 5) наибольшее значение: у=1; наименьшее значение у=-1 Функция кусочно- постоянная Пример 10 Исследовать и построить график функции у=
1)D(f)=(0; 1)∪ (1; +∞ )® y=-1+1®y=0 2)E(f)={0)
Постоянная Пример 11 Исследовать и построить график функции у= Решение: 1)D(f)=(-∞; -1)∪ (-1; 0)∪ (0; 1)∪ (1; +∞ ) у= « y=2-2x Вычислим значения функции в точках разрыва (выколотые точки) у(-1)=4; у(0)=2; у(1)=0® E(f)=(-∞; 0)∪ (0; 2)∪ (2; 4)∪ (4; +∞ ) Корней нет 4) функция общего вида: f(x)≠ Строго убывает Экстремумов нет
Пример 12 (самостоятельно) Исследовать и построить график функции: у=2- Пример 13 (самостоятельно) Исследовать и построить график функции: у= Пример 14 (самостоятельно) Исследовать и построить график функции: у= Пример 15 (самостоятельно) Исследовать и построить график функции: у= ГЛАВА 6. Построение линий и областей на плоскости, заданных уравнениями и неравенствами. Примечание. F(x, y)=0-уравнение линии, если координаты любой точки на линии и только они, удовлетворяют этому уравнению. Неравенство F(x; y)³ 0 (F(x; y)≤ 0)определяет область на координатной плоскости с границей F(x; y)=0, если все точки этой области и только они, удовлетворяют данному неравенству. |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 594; Нарушение авторского права страницы