
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Найти аналитическое выражение функции
y=f(g(𝛗 (x))), построить график и провести исследование. Ответ: у= Обратные функции. Примечание: Основные понятия об обратной функции Были рассмотрены в главе 4. Пример 1. Найти D(f-1) по заданной функции y=f(x), если у= Решение: Т.к функция у= D(f-1)=E(f)®E(f)=(-2; +∞ )=D(f-1). Ответ: (-2; +∞ ). Пример 2. Найти D(f-1) по заданной функции y=f(x), если у= Решение: Т.к. функция у= D(f-1)=E(f)®E(f)=[2; +∞ )=D(f-1). Ответ: [2; +∞ ). Пример 3. Найти D(f-1) по заданной функции y=f(x), если у=5-(х+2)3. Решение: Т.к. функция у=5-(х+2)3.строго убывает на всей числовой оси, то существует обратная функция и при этом: D(f-1)=E(f)®E(f)=(-∞; +∞ )=D(f-1). Ответ: (-∞; +∞ ). Пример 4. Найти D(f-1) по заданной функции y=f(x), если у= Решение: Т.к. функция у= D(f-1)=E(f)®E(f)=(-∞; +∞ )=D(f-1). Ответ: (-∞; +∞ ). Пример 5 (самостоятельно). Найти D(f-1) по заданной функции y=f(x), если у=4- Ответ: (-∞; 4). Пример 6(самостоятельно). Найти D(f-1) по заданной функции y=f(x), если у= Ответ: [-5; +∞ ). Пример 7 (самостоятельно). Найти D(f-1) по заданной функции y=f(x), если у=3- Ответ: (-∞; +∞ ) Пример 8 (самостоятельно). Найти D(f-1) по заданной функции y=f(x), если у= Ответ: [5; +∞ ). Пример 9. Найти E(f-1)по заданной функции у=f(x), если у=3- Решение: Функция у=3- Данная функция строго монотонна, а именно, возрастает. Сделаем контрольную проверку. Пусть х1=3® f(3)=3; x2=2®f(2)=2. x1> x2®f(x1)> f(x2)®функция возрастает. Следовательно, существует обратная функция, при этом E(f-1)=D(f)=(-∞; 4). Ответ: (-∞; 4). Пример 10. Найти E(f-1)по заданной функции у=f(x), если у= Решение: Функция у= Данная функция строго монотонна, а именно убывает. Сделаем контрольную проверку. Пусть х1=2® f(2)=1; x2=-2®f(-2)=3. x1> x2®f(x1)< f(x2)®функция убывает. Следовательно, существует обратная функция, при этом E(f-1)=D(f)=(-∞; 2, 5] Ответ: (-∞; 2, 5]. Пример 11. Найти E(f-1)по заданной функции у=f(x), если у= Решение: Функция у=
Следовательно, существует обратная функция, при этом E(f-1)=D(f)=(-∞; - 5)∪ (-5; +∞ ) Ответ: )=(-∞; - 5)∪ (-5; +∞ ) Пример 12. Найти E(f-1)по заданной функции у=f(x), если у= Решение: Функция у= Данная функция строго монотонна, а именно убывает. Сделаем контрольную проверку. Пусть х1=2® f(2)=-1; x2=1®f(1)=6. x1> x2®f(x1)< f(x2)®функция убывает. Следовательно, существует обратная функция, при этом E(f-1)=D(f)=(-∞; Ответ: (-∞; Пример 13 (самостоятельно). Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞; - Пример 14 (самостоятельно). Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞; Пример 15. Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞; 5, 5]. Пример 16 (самостоятельно). Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞; +∞ ). Пример 17. Дано: у= Найти: 1)обратную функцию; 2) построить графики функций f(x)и f-1(x). Решение: 1.Построим график функции у=
2.D(f)=(-∞; +∞ ) 3.E(f)=(-2; +∞ ); у=-2-горизонтальная асимптота. Функция непрерывная и строго возрастает Существует обратная функция. Находим формулу обратной функции, выражая переменную х через у. у= 6.Для построения графика обратной функции в старой системе координат поменяем местами переменные: х«у: у= 7.D(f-1)=E(f)=(-2; +∞ ); х=-2-вертикальная асимптота. 8.E(f-1)=D(f)=(-∞; +∞ ). 9.f-1 возрастает и непрерывна. Напомним, что графики взаимно обратных функций симметричны относительно прямой у=х. Пример 18. Дано: y= Найти: 1)обратную функцию; 2) построить графики функций f(x)и f-1(x). Решение:
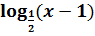 +2 +2
2.D(f)=(1; +∞ ); x=1-вертикальная асимптота. 3.E(f)=(-∞; +∞ ). Функция непрерывна и строго убывает. Существует обратная функция. Находим формулу обратной функции, выражая переменную х через у. y= Для построения графика обратной функции в старой системе координат поменяем местами переменные: х«у =( 7.D(f-1)=E(f)=(-∞; +∞ ). 8.E(f-1)=D(f)=(1; +∞ ); y=1-горизонтальная асимптота. Функция непрерывна и убывает. Пример 19. Дано: у=х2-7х+12. Определить интервалы монотонности и на каждом интервале найти обратную функцию. Построить графики. Решение: у=х2-7х+12«у=(х-3, 5)2-0, 25-это парабола. ü х=3, 5- ось симметрии ü (3, 5; -0, 25)-вершина параболы ü корни: х1=3; х2=4. ü у(0)=12.
|
Последнее изменение этой страницы: 2017-03-14; Просмотров: 1347; Нарушение авторского права страницы