
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Все условия существования обратной функции выполнены.⇐ ПредыдущаяСтр 16 из 16
Если f(x)=tgx (y=tg x), то: 1.D(f)=(- 2.E(f)=(-∞; +∞ ); прямые х=-π /2 и х=π /2- вертикальные асимптоты. Возрастает и непрерывна.
4.Формула обратной функции: f-1: x=arctgy. X«y y=arctg x. Исследование: 1.Область определения: (-∞; +∞ ). 2.Множество значений функции: (- Прямые у=-π /2 и у=π /2-горизонтальные асимптоты. 3.arctgx=0« x=tg0«x=0. 4.arctg(-x)=-arctg x®нечётная функция. 5.С возрастанием х от -∞ до+∞ функция возрастает от –π /2 до +π /2.
§10.Функция у=arcctg x. Определение:
Все условия существования обратной функции выполнены. Если f(x)=ctg x (y=ctg x), то: 1.D(f)=(0; π ), прямые х=0 и х=π - вертикальные асимптоты. 2.E(f)=(-∞; +∞ ). Убывает и непрерывна.
4.Формула обратной функции: f-1: x=arcctg x. X«y y=arcctg x. Исследование: 1.Область определения функции: (-∞; +∞ ). 2.Множество значений функции: (0; π ); прямые у=0 и у=π -горизонтальные асимптоты. 3.Корней нет, т.к. у≠ 0; у(0)=π /2. Функция общего вида. Справедлива формула: arcctg(-x)=π - arcctg x. 5.Если х возрастает от -∞ до +∞, то функция убывает от π до 0.
§11.Решение примеров. Пример1 Найти область определения следующих функций 1) 3) 5) 7) Решения 1) Заметим, что: Область определения функции:
Ответ: {( 2) Заметим, что Область определения:
Ответ: 3) Заметим, что: Тогда: Область определения функции: - Ответ: 4) Область определения функции:
Ответ: 5) Область определения функции:
Ответ: 6) Область определения функции:
Ответ: 7) Область определения функции:
Ответ: Пример 2. Найти область определения следующих функций (самостоятельно) 1) 3) 5) 7) Ответы: 1)D(y)={( 3) 5) 7) Пример 2. Найти множество значений функции E(f) и точки экстремумов. 1) f(x)=cos2x + cosx –3/4; 2) f(x)=cos2x + 3) f(x)= -4cos2x + 4 Решение: 1) f(x)=cos2x + cosx –3/4 Введем новую переменную t=cosx, t Є [-1, 1] f(t)= t2 +t – ¾ è f(t)= (t+1/2)2-1, t Є [-1, 1] (рис1) min f|t=-1/2= -1 è m=-1; f(-1)=-3/4; f(1)= 5/4 è M=5/4 E(f)= [-1; 1 Ответ: E(f)= [-1; 1 2) f(x)=cos2x + Введем новую переменную: t=cosx, t Є [-1, 1]
minf|t=- = 1 - f(1)= (1 + M= minf=-2 при t= Ответ: E(f)= [-2; Рис.2 3) f(x)= -4cos2x+4√ 3 cosx
f(t)= -4t2+4√ 3 t, t Є [-1, 1] f(t)=-4(t- maxf|t= f(-1)= -4 - 4 f(1)= -4+ 4 E(f)=[ -4 - 4 maxf=3 при t= Ответ: E(f)=[ -4 - 4 Пример 3 (самостоятельно) Найти множество значений функции E(f) и точки экстремумов (самостоятельно) 2) f(x)= -2 sin2x+ 2 3) f(x)=4sin2x +4 Ответ: 1) E(f)= [-1 2) E(f)=[- 2 3) E(f)=[-5; 2+4
Пример 4. Решить уравнение: | Решение: Обозначим |t- Геометрическое решение: (Повторите в разделе «специальные функции» функцию «корыто»)
 «- «-  «- «- 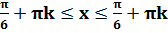 ; kÎ Z. ; kÎ Z.
Ответ: {[- Пример 5 (самостоятельно). | Ответ: {2π k, kÎ Z}. Пример 6. Решить неравенство:
Решение: Рассмотрим две функции: f(x)= f(x)³ g(x). Определим множество значений для каждой функции: f(x)= g(x)= 1≤ f(x)³ g(x) « « Ответ: { Пример 7 Самостоятельно). Решить неравенство:
Ответ: { Пример 8. Найти область определения функции: y=arcsin(3x+4). Решение: Область определения данной функции: |3х+4|≤ 1«|х+
Ответ: D(f)=[- Пример 9 (самостоятельно). Найти область определения функции: y=arccos(2-5x). Ответ: [1/5; 3/5]. Пример 10. Решить уравнение:
Решение: О.д.з.: |х2-8|≤ 1«7≤ х2≤ 9« √ 7≤ |х|≤ 3.
О.д.з.: хÎ [-3; -√ 7]∪ [√ 7; 3]. Т.к. x2-8+3x2+16x+8=0 « 4x2+16x=0« x(x+4)=0« Ответ: ∅ Пример 11(самостоятельно). Решить уравнение:
Ответ: {2}. Пример 12 (самостоятельно). Вычислить: Ответ: √ 5. Пример 13 (самостоятельно). Вычислить: |3 Ответ: 5 Пример 14. Вычислить: 1) 2) 3) 4) Решение: 1) Пусть arctg(
Ответ:
Пусть arcctg(1/√ 7)=𝛂 «
Ответ: 3) Пусть
Ответ: -2. 1) 4) Пусть
Ответ: - Пример 15 (самостоятельно) Вычислить: 1) 2) tg(arcctg(-2/5); 3) 4) 5) tg(arc 6) ctg(arc Ответ: 1) Пример 14. Найти периоды данных функций и вычислить значения функций в указанных точках. 1. y= 2 sin 2. y= - 3. y= 5 tg 4. y= 5. y= 2 sin3x+1; х1= 6. y= 4 cos 7. y=sin2x; х1= 8. y=cos2 2x; х1= Решение: Заметим, что для функций y=sin x и y=cos x основной период Т=2 Для функций y=tg x и y=ctg x основной период Т= |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 629; Нарушение авторского права страницы