
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Покажем, что число 2L - тоже период этой функции.
∀ xÎ X, x±LÎ X®x±2LÎ X f(x+2L)=f((x+L)+L)=f(x+L)=f(x) f(x+2L)=f(x)
Определение: Наименьшее положительное число из множества всех периодов называется основным периодом, который мы будем обозначать Т. Напомним основные периоды для тригонометрических функций: 1) y=sin x, T=2π (sin(x±2π )=sin x) 2) y=cosx, T=2π (cos(x 3) y=tgx, T=π (tg(x 4) y=ctgx, T=π (ctg(x
При построении графика периодической функции можно сначала построить график на интервале длины T, а затем периодически продолжить график на всю числовую ось. Замечание: Если y=f(x) – чётная, то строим график на интервале [0; Затем чётным образом на интервале [- Аналогично для нечётной функции, только на интервале [- 3. Если функция y=f(x) имеет период Т, то функция y=Аf(kx+b)+ B имеет период (А, В, k, b) – постоянные) 4. Если функция f1(x) имеет период Т1, функция f2(x) имеет период Т2, то функция y=Аf1(x)+ B f2(x) тоже периодическая с периодом T. Для нахождения T используем соотношение: kТ1=nТ2 (k, n Тогда, Т= Определение тригонометрических функций. Рассмотрим окружность, заданную уравнением: х2+у2=1; R=1. (В дальнейшем будем называть эту окружность тригонометрической). Пусть радиус-вектор Пусть координаты точки М(х.; у).
Определение: R=1®
Ось (оу) называют осью синусов.
R=1®
Ось (ох) называют осью косинусов. Таким образом, точка М на тригонометрической окружности имеет координаты М( Замечание: Аргументом синуса и косинуса является угол поворота 𝛂. Если этот угол выражается в радианах, то значениями 𝛂 являются действительные числа. Напомним, что радиан ( от лат radius) можно определить как центральный угол, который опирается на дугу, равную радиусу.
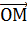
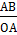 =tg𝛂, т.к. ОА=1® =tg𝛂, т.к. ОА=1®
tgα =AB. Прямая х=1 называется осью тангенсов.
Рассмотрим прямую у=1.
В-точка пересечения Тогда Прямая у=1 называется осью котангенсов. §3. Функция у= Исследование: 1. D(f)=(-∞; +∞ ). 2. E(f)=[-1; 1]. 3. 4. 5. Основной период Т=2π; Т.к. функция нечётная и периодическая, то достаточно исследовать функцию на интервале [0; π ]. 6.Если х возрастает от 0 доπ /2, то функция возрастает от 0 до 1. Если х возрастает от π /2 до π, то функция убывает от 1до 0. 7.min y=-1; max y=1; График функции называется синусоидой.
§4. Функция у= 1. D(f)=(-∞; +∞ ). 2. E(f)=[-1; 1]. 3. 4. 5. Основной период Т=2π; Т.к. функция чётная и периодическая, то достаточно исследовать функцию на интервале [0; π ]. 6.Если х возрастает от 0 до π, то функция убывает от 1 до -1. 7.min y=-1; max y=1; График функции называется косинусоидой.
§5.Функция y=tg x. Исследование: y=tg x «у= 1. D(f): Прямые х=π /2 +π к, кÎ Z-вертикальные асимптоты. 2. E(f)=(-∞; +∞ ). 3. tgx=0« 4. tg(-x)=-tgx®нечётная функция. 5. Периодическая, основной период Т=𝛑. tg(x±𝛑 )=tgx. 6. На интервале (-π /2; π /2) функция возрастает от -∞ до +∞. Экстремумов нет. График функции называется тангенсоидой.
§6. Функция у=ctg x. Исследование: y=ctg x« y= 1. D(f): 2. E(f)=(- ∞; +∞ ). 3. ctg x=0« 4. ctg(-x)=-ctg x®нечётная функция. 5. Периодическая, основной период Т=𝛑. сtg(x±𝛑 )=сtgx. 6. На интервале (0; π ) функция убывает от +∞ до -∞. Экстремумов нет. График функции называется котангенсоидой.
§7. Функция y=arcsin x. Определение:
Рассмотрим функцию у= Все условия существования обратной функции выполнены. Действительно, если f(x)= 1.D(f)=[-π /2; π /2].
Возрастает и непрерывна. 4.Формула обратной функции: f-1: x=
Исследование: 1.Область определения: [-1; 1]. 2.Множество значений: [-π /2; π /2]. 3.arcsin x=0«x= 4.arcsin(-x)=-arcsin x® нечётная функция. 5.Если х возрастает от -1 до +1, то функция возрастает от – Экстремумов нет.
 ; у(наиб.)(1)= ; у(наиб.)(1)=  . .
§8. Функция у=arсcos x. Определение:
Рассмотрим функцию у= Все условия существования обратной функции выполнены.
 (y= (y= 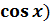 , то: , то:
4.Формула обратной функции: f-1: x=arсcos y X«y y=arсcos x. Исследование: 1.Область определения функции: [-1; 1]. 2.Множество значений функции: [0; π ]. 3.arccos x=0 «x= Функция общего вида. Справедлива формула: arсcos(-x)=𝛑 - arccos x 5.Если х возрастает от -1 до 1, то функция убывает от π до 0. Экстремумов нет
§9. Функция у=arctg x. Определение:
Рассмотрим функцию у=tg x на интервале (- |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 438; Нарушение авторского права страницы