Расчет переходного процесса методом трапеций
Вещественную частотную характеристику (рисунок 10) заменим мало отличающимися от кривой горизонтальными и наклонными прямолинейными участками, образующими с осью ординат трапеции. Действительная ВЧХ при этом будет представлена как алгебраическая сумма трапецеидальных частотных характеристик
, (3.6)
где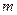 
‑ число трапеций.
Горизонтальные отрезки чертим в точках экстремумов. Первый отрезок должен начинаться из точки 
, т.к. эта точка определяет конечное значение переходной характеристики 
. Более тщательно нужно аппроксимировать начальный участок ВЧХ. Конечный участок с ординатами, меньшими по абсолютному значению, чем 
можно не принимать во внимание. Проиллюстрируем все вышесказанное (рисунок 11).
Рисунок 11 – Замена вещественной частотной характеристики трапециями
Полученные трапеции вычертим на другом чертеже (рисунок 12) таким образом, чтобы основание каждой из них легло на ось 
.
Рисунок 12 – Трапеции вещественной частотной характеристики
Определим параметры трапеций.
Из графиков находим
,
.
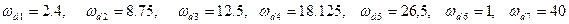
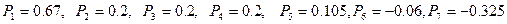По значениям 
вычислим коэффициенты наклона
(3.7)
и округлим их до ближайшего из значений 0; 0, 05; 0, 1; 0, 15; … 0, 95; 1.
Подставив численные значения, получим
.
Рассчитаем переходные процессы отдельно для каждой трапеции.
В таблице h-функций таблица 4.2 с.222 [3] для каждой i-й трапеции отыскивается столбец, соответствующий значению коэффициента наклона 
. Затем для ряда значений условного времени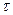 
выписывают соответствующие им значения 
. По значениям 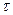и вычисляют значения действительного времени 
и составляющей переходной характеристики 
:
; 
. (3.8)
Результаты оформим в таблице 5.
Таблица 5 – Расчет графиков составляющих переходной характеристики
| Трапеция 1
| Трапеция 2
| Трапеция 3
|
| 
| 
|
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
|
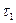
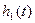
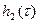
| 0.0
| 0.000
| 0.000
| 0.000
| 0.0
| 0.000
| 0.00
| 0.000
| 0.0
| 0.000
| 0.000
| 0.000
|
| 0.5
| 0.199
| 0.057
| 0.133
| 0.5
| 0.267
| 0.04
| 0.0534
| 0.5
| 0.267
| 0.028
| 0.0534
|
| 1.0
| 0.386
| 0.114
| 0.259
| 1.0
| 0.519
| 0.08
| 0.1145
| 1.0
| 0.519
| 0.055
| 0.1145
|
| 1.5
| 0.56
| 0.171
| 0.375
| 1.5
| 0.740
| 0.12
| 0.1480
| 1.5
| 0.740
| 0.083
| 0.1480
|
| 2.0
| 0.709
| 0.228
| 0.475
| 2.0
| 0.919
| 0.16
| 0.1840
| 2.0
| 0.919
| 0.1103
| 0.1840
|
| 2.5
| 0.833
| 0.343
| 0.558
| 2.5
| 1.042
| 0.20
| 0.2084
| 2.5
| 1.042
| 0.138
| 0.2084
|
| 3.0
| 0.928
| 0.400
| 0.622
| 3.0
| 1.130
| 0.24
| 0.226
| 3.0
| 1.130
| 0.165
| 0.226
|
| 3.5
| 0.991
| 0.457
| 0.666
| 3.5
| 1.161
| 0.28
| 0.2322
| 3.5
| 1.161
| 0.193
| 0.2322
|
| 4.0
| 1.009
| 0.514
| 0.670
| 4.0
| 1.100
| 0.32
| 0.220
| 4.0
| 1.100
| 0.22
| 0.220
|
| 4.5
| 1.057
| 0.571
| 0.708
| 4.5
| 1.132
| 0.36
| 0.2264
| 4.5
| 1.132
| 0.248
| 0.2264
|
| 5.0
| 1.067
| 0.628
| 0.715
| 5.0
| 1.081
| 0.40
| 0.2168
| 5.0
| 1.081
| 0.276
| 0.2168
|
| 5.5
| 1.067
| 0.686
| 0.715
| 5.5
| 1.032
| 0.44
| 0.2064
| 5.5
| 1.032
| 0.303
| 0.2064
|
| 6.0
| 1.054
| 0.743
| 0.706
| 6.0
| 0.984
| 0.48
| 0.1968
| 6.0
| 0.984
| 0.331
| 0.1968
|
| 6.5
| 1.043
| 0.800
| 0.699
| 6.5
| 0.927
| 0.52
| 0.1896
| 6.5
| 0.927
| 0.359
| 0.1896
|
| 7.0
| 1.035
| 0.857
| 0.693
| 7.0
| 0.922
| 0.56
| 0.1854
| 7.0
| 0.922
| 0.386
| 0.1854
|
| 7.5
| 1.025
| 0.914
| 0.687
| 7.5
| 0.932
| 0.60
| 0.1844
| 7.5
| 0.932
| 0.414
| 0.1844
|
| 8.0
| 1.024
| 0.971
| 0.686
| 8.0
| 0.951
| 0.66
| 0.1864
| 8.0
| 0.951
| 0.441
| 0.1864
|
| 8.5
| 1.022
| 1.085
| 0.685
| 8.5
| 1.000
| 0.68
| 0.1902
| 8.5
| 1.000
| 0.469
| 0.1902
|
| 9.5
| 1.027
| 1.143
| 0.688
| 9.5
| 1.020
| 0.76
| 0.200
| 9.5
| 1.020
| 0.524
| 0.200
|
| 10.0
| 1.027
| 1.200
| 0.688
| 10.0
| 1.033
| 0.80
| 0.204
| 10.0
| 1.033
| 0.552
| 0.204
|
| 10.5
| 1.028
| 1.257
| 0.689
| 10.5
| 1.039
| 0.84
| 0.2066
| 10.5
| 1.039
| 0.579
| 0.2066
|
| 11.0
| 1.025
| 1.314
| 0.687
| 11.0
| 1.037
| 0.88
| 0.2078
| 11.0
| 1.037
| 0.607
| 0.2078
|
| 11.5
| 1.021
| 1.485
| 0.684
| 11.5
| 1.027
| 0.92
| 0.2074
| 11.5
| 1.027
| 0.634
| 0.2074
|
| 12.0
| 1.015
| 1.543
| 0.680
| 12.0
| 1.005
| 0.96
| 0.2054
| 12.0
| 1.005
| 0.662
| 0.2054
|
| 13.0
| 1.005
| 1.600
| 0.673
| 13.0
| 0.995
| 1.04
| 0.201
| 13.0
| 0.995
| 0.717
| 0.201
|
| 13.5
| 1.000
| 1.714
| 0.670
| 13.5
| 0.987
| 1.08
| 0.1990
| 13.5
| 0.987
| 0.745
| 0.1990
|
| 14.0
| 0.997
| 1.828
| 0.686
| 14.0
| 0.983
| 1.12
| 0.1974
| 14.0
| 0.983
| 0.772
| 0.1974
|
| 15.0
| 0.995
| 1.885
| 0.666
| 15.0
| 0.990
| 1.20
| 0.1966
| 15.0
| 0.990
| 0.828
| 0.1966
|
| 16.0
| 0.995
| 1.943
| 0.666
| 16.0
| 0.995
| 1.28
| 0.198
| 16.0
| 0.995
| 0.883
| 0.198
|
| 16.5
| 0.995
| 2.000
| 0.666
| 16.5
| 0.990
| 1.32
| 0.199
| 16.5
| 0.990
| 0.910
| 0.199
|
| 17.0
| 0.995
| 2.075
| 0.666
| 17.0
| 1.012
| 1.36
| 0.2024
| 17.0
| 1.012
| 0.938
| 0.2024
|
| 17.5
| 0.995
| 2.114
| 0.666
| 17.5
| 1.004
| 1.40
| 0.2008
| 17.5
| 1.004
| 0.966
| 0.2008
|
| 18.0
| 0.995
| 2.171
| 0.666
| 18.0
| 1.003
| 1.44
| 0.2006
| 18.0
| 1.003
| 0.993
| 0.2006
|
| 18.5
| 0.994
| 2.285
| 0.665
| 18.5
| 1.004
| 1.48
| 0.2008
| 18.5
| 1.004
| 1.02
| 0.2008
|
| 19.0
| 0.992
| 2.343
| 0.664
| 19.0
| 1.003
| 1.52
| 0.2006
| 19.0
| 1.003
| 1.048
| 0.2006
|
| 20.0
| 0.991
| 2.400
| 0.668
| 20.0
| 1.001
| 1.60
| 0.2002
| 20.0
| 1.001
| 1.103
| 0.2002
|
| 20.5
| 0.991
| 2.571
| 0.668
| 20.5
| 0.999
| 1.64
| 0.1998
| 20.5
| 0.999
| 1.131
| 0.1998
|
| 21.0
| 0.992
| 2.628
| 0.664
| 21.0
| 0.996
| 1.68
| 0.1992
| 21.0
| 0.996
| 1.159
| 0.1992
|
| 22.5
| 0.995
| 2.685
| 0.666
| 22.5
| 0.997
| 1.80
| 0.1994
| 22.5
| 0.997
| 1.241
| 0.1994
|
| 23.0
| 0.997
| 2.743
| 0.666
| 23.0
| 0.998
| 1.84
| 0.1996
| 23.0
| 0.998
| 1.269
| 0.1996
|
| 23.5
| 0.998
| 2.800
| 0.669
| 23.5
| 0.999
| 1.88
| 0.998
| 23.5
| 0.999
| 1.296
| 0.998
|
| 24.0
| 0.999
| 2.857
| 0.669
| 24.0
| 1.000
| 1.92
| 0.20
| 24.0
| 1.000
| 1.324
| 0.20
|
| 24.5
| 0.999
| 2.901
| 0.669
| 24.5
| 0.998
| 1.96
| 0.996
| 24.5
| 0.998
| 1.352
| 0.996
|
| 25.0
| 0.999
| 2.903
| 0.669
| 25.0
| 1.001
| 2.00
| 0.2002
| 25.0
| 1.001
| 1.379
| 0.2002
|
Продолжение таблицы 5
| Трапеция 4
| Трапеция 5
|
| 
|
| 
|
| 
| 
| 
|
| 
|
| 0.0
| 0.000
| 0.000
| 0.000
| 0.0
| 0.000
| 0.000
| 0.000
|
| 0.5
| 0.267
| 0.019
| 0.0534
| 0.5
| 0.111
| 0.005
| 0.012
|
| 1.0
| 0.519
| 0.038
| 0.1145
| 1.0
| 0.222
| 0.011
| 0.023
|
| 1.5
| 0.740
| 0.057
| 0.1480
| 1.5
| 0.329
| 0.017
| 0.035
|
| 2.0
| 0.919
| 0.075
| 0.1840
| 2.0
| 0.433
| 0.023
| 0.045
|
| 2.5
| 1.042
| 0.094
| 0.2084
| 2.5
| 0.534
| 0.029
| 0.056
|
| 3.0
| 1.130
| 0.113
| 0.226
| 3.0
| 0.628
| 0.034
| 0.066
|
| 3.5
| 1.161
| 0.132
| 0.2322
| 3.5
| 0.716
| 0.04
| 0.075
|
| 4.0
| 1.100
| 0.151
| 0.220
| 4.0
| 0.798
| 0.046
| 0.084
|
| 4.5
| 1.132
| 0.17
| 0.2264
| 4.5
| 0.872
| 0.051
| 0.092
|
| 5.0
| 1.081
| 0.189
| 0.2168
| 5.0
| 0.938
| 0.057
| 0.098
|
| 5.5
| 1.032
| 0.207
| 0.2064
| 5.5
| 0.996
| 0.063
| 0.105
|
| 6.0
| 0.984
| 0.226
| 0.1968
| 6.0
| 1.045
| 0.069
| 0.11
|
| 6.5
| 0.927
| 0.245
| 0.1896
| 6.5
| 1.086
| 0.074
| 0.114
|
| 7.0
| 0.922
| 0.264
| 0.1854
| 7.0
| 1.119
| 0.08
| 0.117
|
| 7.5
| 0.932
| 0.283
| 0.1844
| 7.5
| 1.143
| 0.086
| 0.112
|
| 8.0
| 0.951
| 0.302
| 0.1864
| 8.0
| 1.16
| 0.091
| 0.122
|
| 8.5
| 1.000
| 0.321
| 0.1902
| 8.5
| 1.169
| 0.097
| 0.123
|
| 9.5
| 1.020
| 0.359
| 0.200
| 9.5
| 1.172
| 0.1
| 0.123
|
| 10.0
| 1.033
| 0.377
| 0.204
| 10.0
| 1.169
| 0.108
| 0.122
|
| 10.5
| 1.039
| 0.396
| 0.2066
| 10.5
| 1.161
| 0.114
| 0.121
|
| 11.0
| 1.037
| 0.415
| 0.2078
| 11.0
| 1.148
| 0.12
| 0.12
|
| 11.5
| 1.027
| 0.434
| 0.2074
| 11.5
| 1.131
| 0.126
| 0.118
|
| 12.0
| 1.005
| 0.453
| 0.2054
| 12.0
| 1.112
| 0.131
| 0.117
|
| 13.0
| 0.995
| 0.49
| 0.201
| 13.0
| 1.092
| 0.137
| 0.115
|
| 13.5
| 0.987
| 0.509
| 0.1990
| 13.5
| 1.069
| 0.143
| 0.11
|
| 14.0
| 0.983
| 0.528
| 0.1974
| 14.0
| 0.966
| 0.171
| 0.101
|
| 15.0
| 0.990
| 0.566
| 0.1966
| 15.0
| 0.917
| 0.2
| 0.096
|
| 16.0
| 0.995
| 0.603
| 0.198
| 16.0
| 0.996
| 0.229
| 0.105
|
| 16.5
| 0.990
| 0.623
| 0.199
| 16.5
| 0.990
| 0.257
| 0.104
|
| 17.0
| 1.012
| 0.642
| 0.2024
| 17.0
| 1.036
| 0.286
| 0.109
|
| 17.5
| 1.004
| 0.66
| 0.2008
| 17.5
| 1.047
| 0.314
| 0.11
|
| 18.0
| 1.003
| 0.679
| 0.2006
| 18.0
| 1.025
| 0.343
| 0.107
|
| 18.5
| 1.004
| 0.698
| 0.2008
| 18.5
| 0.993
| 0.371
| 0.104
|
| 19.0
| 1.003
| 0.717
| 0.2006
| 19.0
| 0.975
| 0.4
| 0.102
|
| 20.0
| 1.001
| 0.755
| 0.2002
| 20.0
| 0.977
| 0.429
| 0.105
|
| 20.5
| 0.999
| 0.773
| 0.1998
| 20.5
| 0.993
| 0.457
| 0.104
|
| 21.0
| 0.996
| 0.792
| 0.1992
| 21.0
| 1.008
| 0.486
| 0.117
|
| 22.5
| 0.997
| 0.849
| 0.1994
| 22.5
| 1.014
| 0.514
| 0.106
|
| 23.0
| 0.998
| 0.868
| 0.1996
| 23.0
| 1.009
| 0.543
| 0.101
|
| 23.5
| 0.999
| 0.887
| 0.998
| 23.5
| 1.001
| 0.571
| 0.105
|
| 24.0
| 1.000
| 0.906
| 0.20
| 24.0
| 0.996
| 0.6
| 0.104
|
| 24.5
| 0.998
| 0.925
| 0.996
| 24.5
| 0.995
| 0.629
| 0.106
|
| 25.0
| 1.001
| 0.943
| 0.2002
| 25.0
| 0.997
| 0.657
| 0.108
|
Продолжение таблицы 5
| Трапеция 6
| Трапеция 7
|
| 
|
| 
|
| 
| 
| 
|
| 
|
| 0.0
| 0.000
| 0.000
| 0.000
| 0.0
| 0.000
| 0.000
| 0.000
|
| 0.5
| 0.223
| 0.208
| -0.134
| 0.5
| 0.102
| 0.003
| -0.033
|
| 1.0
| 0.432
| 0.416
| -0.267
| 1.0
| 0.203
| 0.006
| -0.066
|
| 1.5
| 0.617
| 0.625
| -0.037
| 1.5
| 0.302
| 0.009
| -0.098
|
| 2.0
| 0.786
| 0.833
| -0.047
| 2.0
| 0.396
| 0.012
| -0.129
|
| 2.5
| 0.938
| 1.042
| -0.056
| 2.5
| 0.491
| 0.015
| -0.16
|
| 3.0
| 1.010
| 1.25
| -0.0606
| 3.0
| 0.579
| 0.018
| -0.188
|
| 3.5
| 1.074
| 1.46
| -0.0644
| 3.5
| 0.662
| 0.022
| -0.215
|
| 4.0
| 1.107
| 1.666
| -0.06642
| 4.0
| 0.741
| 0.025
| -0.241
|
| 4.5
| 1.115
| 1.875
| -0.0669
| 4.5
| 0.812
| 0.028
| -0.264
|
| 5.0
| 1.095
| 2.083
| -0.0667
| 5.0
| 0.878
| 0.03
| -0.285
|
| 5.5
| 1.068
| 2.29
| -0.0657
| 5.5
| 0.936
| 0.034
| -0.3042
|
| 6.0
| 1.043
| 2.50
| -0.06408
| 6.0
| 0.988
| 0.037
| -0.3211
|
| 6.5
| 1.023
| 2.708
| -0.0626
| 6.5
| 1.032
| 0.04
| -0.3354
|
| 7.0
| 1.005
| 2.917
| -0.0614
| 7.0
| 1.069
| 0.043
| -0.3474
|
| 7.5
| 0.995
| 3.125
| -0.0603
| 7.5
| 1.100
| 0.046
| -0.358
|
| 8.0
| 0.992
| 3.33
| -0.0595
| 8.0
| 1.123
| 0.049
| -0.365
|
| 8.5
| 0.992
| 3.54
| -0.0595
| 8.5
| 1.141
| 0.052
| -0.371
|
| 9.5
| 0.993
| 3.75
| -0.0596
| 9.5
| 1.153
| 0.055
| -0.374
|
| 10.0
| 0.993
| 3.96
| -0.0596
| 10.0
| 1.157
| 0.058
| -0.376
|
| 10.5
| 0.992
| 4.17
| -0.0595
| 10.5
| 1.158
| 0.061
| -0.3763
|
| 11.0
| 0.993
| 4.375
| -0.0596
| 11.0
| 1.154
| 0.065
| -0.3727
|
| 11.5
| 0.991
| 4.580
| -0.0594
| 11.5
| 1.147
| 0.068
| -0.3692
|
| 12.0
| 0.988
| 4.792
| -0.0593
| 12.0
| 1.136
| 0.07
| -0.3646
|
| 13.0
| 0.986
| 5.00
| -0.05916
| 13.0
| 1.122
| 0.074
| -0.3598
|
| 13.5
| 0.985
| 5.208
| -0.0591
| 13.5
| 1.107
| 0.077
| -0.311
|
| 14.0
| 0.984
| 5.42
| -0.059
| 14.0
| 1.020
| 0.092
| -0.306
|
| 15.0
| 0.996
| 5.625
| -0.05976
| 15.0
| 0.957
| 0.108
| -0.3123
|
| 16.0
| 0.998
| 5.83
| -0.05988
| 16.0
| 0.941
| 0.123
| -0.3227
|
| 16.5
| 1.002
| 6.04
| -0.0601
| 16.5
| 0.961
| 0.138
| -0.3295
|
| 17.0
| 1.005
| 6.25
| -0.0603
| 17.0
| 0.993
| 0.154
| -0.33
|
| 17.5
| 1.006
| 6.46
| -0.06036
| 17.5
| 1.014
| 0.169
| -0.3289
|
| 18.0
| 1.008
| 6.66
| -0.06048
| 18.0
| 1.018
| 0.184
| -0.3266
|
| 18.5
| 1.007
| 6.875
| -0.06042
| 18.5
| 1.012
| 0.2
| -0.3257
|
| 19.0
| 1.005
| 7.08
| -0.0603
| 19.0
| 1.005
| 0.215
| -0.3253
|
| 20.0
| 1.004
| 7.29
| -0.06024
| 20.0
| 1.001
| 0.23
| -0.325
|
| 20.5
| 1.004
| 7.50
| -0.06024
| 20.5
| 1.000
| 0.25
| -0.324
|
| 21.0
| 1.003
| 7.708
| -0.06018
| 21.0
| 0.997
| 0.261
| -0.3227
|
| 22.5
| 1.003
| 8.33
| -0.06018
| 22.5
| 0.993
| 0.277
| -0.3224
|
| 23.0
| 1.002
| 8.54
| -0.06012
| 23.0
| 0.992
| 0.292
| -0.3237
|
| 23.5
| 1.001
| 8.75
| -0.0606
| 23.5
| 0.996
| 0.308
| -0.3272
|
| 24.0
| 1.00
| 9.17
| -0.06
| 24.0
| 1.002
| 0.323
| -0.3272
|
| 24.5
| 0.998
| 9.58
| -0.05988
| 24.5
| 1.007
| 0.338
| -0.3263
|
| 25.0
| 0.997
| 9.79
| -0.5982
| 25.0
| 1.004
| 0.369
| -0.3247
|
Далее построим графики составляющих переходной характеристики . Все составляющие расположим на одном чертеже (рисунок 12) с учетом знака, который определяется знаком высоты 
соответствующей трапеции.
График переходной характеристики замкнутой системы получим путем суммирования ординат всех составляющих в равные моменты времени
. (3.9)
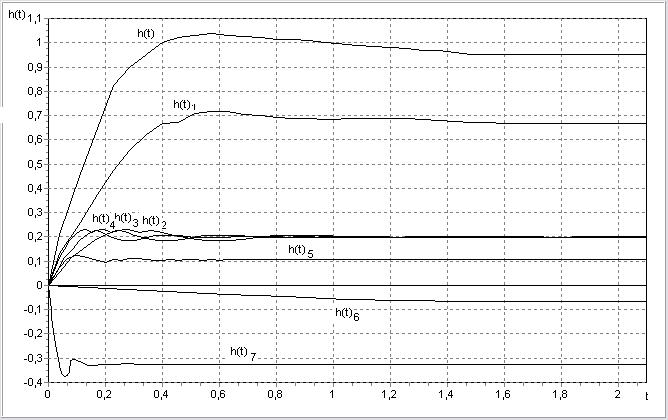
Рисунок 13 – График переходного процесса и его составляющие
Оценка качества переходного процесса
По полученной переходной характеристике скорректированной системы произведем оценку качества переходного процесса.
На рисунке 13 приведена переходная характеристика процесса, который происходит в заданной системе при изменении задающего воздействия в виде единичного скачка 
.
Рисунок 14 – Показатели качества регулирования
На рисунке приняты следующие обозначения:
Переходная функция апериодическая;
‑ значения максимума;
‑ установившееся значение переходной характеристики;
‑ время нарастания;
‑ время достижения первого максимума;
‑ время регулирования;
‑ допустимое отклонение.
Для определения показателей качества регулирования примем
.
Найдем прямые оценки качества регулирования непосредственно из графика:
‑ установившееся значение;
; ‑ время нарастания;
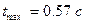; ‑ время достижения первого максимума;
; ‑ время регулирования;
Используя прямые оценки качества регулирования, найдем остальные показатели качества регулирования.
Перерегулирование найдем согласно формуле
, (3.10)
подставив численные значения, получим 
.
Статическая ошибка, определяемая согласно формуле
, (3.11)
будет равна 
.
Выбор схемы и расчет параметров корректирующего устройства
Популярное:
