Линейное программирование. Классификация и свойства задач линейного программирования.

⇐ ПредыдущаяСтр 23 из 51Следующая ⇒

Принципы построения и особенности задач линейного программирования: Линейное программир-е изучает задачу отыскания экстремума линейной ф-ии при наличии огранич-й в виде линейных неравенств или уравнений. Сущность этих задач заключ-ся в том, чтобы из множества возможных вариантов исслед-го экономич-го пр-сса выбрать по какому-либо признаку наилучший/ оптимальный вариант. В этом методе обязателен специальный показ-ль – критерий оптимальности плана. Цель заключ-ся в максимизации или минимизации некоторого кол-ва средств, к-е математ-ки выраж-ся в виде линейной формы некоторого числа переменных. Множ-во возможных вариантов, из к-х выбирается оптимальный план, всегда ограничено. Поэтому каждый из рассматриваемых вариантов д.б. допустимым планом, удовлетворяющим имеющимся ограничениям. Показатель оптимальности плана яв-ся некоторой ф-ей Z=f(x) плана Х. Поэтому задача отыскания оптим-го плана сводится к математической задаче нахождения экстремума этой ф-ии. Построение ЭММ состоит в создании упрощенной экономич-й модели, в к-й схематически отражена сущность изучаемого процесса. Особое внимание д.б. уделено отражению в модели всех существенных особен-тей задачи и учету всех ограничивающих условий, к-е могут повлиять на рез-т. Затем определяют цель реш-я, выбирают критерий оптимальности и дают математическую формулировку задачи.

Общая задача линейного программирования, формы и виды ее записи: Задача вида: найти экстремум (max, min) функции n переменных (1) при условиях: ; наз-ся общей задачей линейного программир-я. В этой зад. линейная ф-я L(x) наз-ся целевой ф-ей, т.к. в ней формулируется цель. Условия (2) и (3) наз-ся ограничениями задачи, к-е налагаются на переменные. Они задают область допустимых значений переменных. При этом усл-е (2) функциональными ограничениями задачи. Усл-е (3) – ограничениями на знак переменных. Они не м.б. отрицательными. Реш-е, удовлетворяющее условиям (2) и (3), наз-ся допустимым. Допустимое реш-е, у к-го в точности m неизвестных отличны от нуля, а остальные переменные = 0, наз-ся опорным/ граничным. Допустимое реш-е, доставляющее экстремум целевой функции, наз-ся оптимальным. Решить задачу линейного программиров-я (ЗЛП) значит найти ее оптимальное реш-е. Оптимальное реш-е ЗЛП яв-ся опорным. 3 вида ЗЛП: 1.Если все функциональные ограничения (2) заданы неравенствами , и все свободные члены 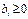, то такая форма записи ЗЛП наз-ся стандартной. 2.ЗЛП задана в каноническом виде, если все ограничения в сис-ме (2) равенствами, и вып-ся условие (3). 3.Если в сис-ме (2) имеются и равенства и неравенства, то такая ЗЛП задана в смешанном виде. Возможен переход от одной записи к другой. Алгоритм преобразования стандартных и смешанных ЗЛП к каноническому виду: 1) - величина, на к-ю меньше 1-е ур-е из (2), чем и т.д. ; , -разница м/у левой и правой частью. (1’) 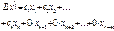; (3’) 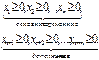2)Если в сис-ме (2) ограничения заданы знаком ³, то в этом ограничении дополнительную переменную следует вычесть из левой части и заменить знак неравинства на равенство. 3)Если 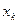не ограничен по знаку, тогда вводим подстановку 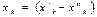, где . Всякая ЗЛП м.б. задана: 1.В развернутом виде, когда расписаны все функциональные ограничения и все переменные, 2.В матричном виде: ; ; ; ; Х, В, С – векторы, тогда целевая функция: ; ; . 3.Записана с использ-ем векторов: 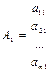; ; …; , тогда целевая ф-я(1) ; (2) ; – это полупространство в векторной записи.

Экономическая иллюстрация на примерах задач оптимального использования ресурсов, рационального раскроя материалов, составления оптимальных смесей и т.п: Задача о раскрое материалов: на раскрой поступает материал одного образца в кол-ве а единиц. Требуется изготовить из него l разных комплектующих изделий в кол-вах, пропорциональных числам (условие комплектности). Каждая единица материала м.б. раскроена n различными способами, причем использование i-го способа (i=1, 2, …, n) дает единиц k-го изделия (k=1, 2, …, l). Необходимо найти план раскроя, обеспечивающий максимальное число комплектов. ЭММ: - число единиц материала, раскраиваемых i-м способом, х – число изготавливаемых комплектов изделий. Т.к. общее кол-во материала равно сумме его ед-ц, раскраиваемых различными способами, то (1). Требование комплектности выразится ур-ем (2). Очевидно, что (3). Найти такое реш-е , удовлетворяющее с/с ур-й (1) – (2) и условию (3), при к-м ф-я F=x принимает максимальное значение. Обобщение на случай m раскраиваемых материалов: Пусть каждая ед-ца j-го (j=1, 2, …, m) матер-ла м.б. раскроена n различными способами, причем использование i-го способа (i=1, 2, …, n) дает единиц k-го изделия (k=1, 2, …, l), а запас j-го материала равен единиц. Обозначим - число ед-ц j-го материала, раскраиваемого i-м способом. ЭММ о раскрое в общей постановке примет вид: найти такое реш-е , удовлетворяющее сис-ме 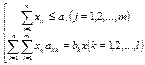и условию , при к-м ф-я F=x принимает максимальное знач-е. Задача об использовании ресурсов (задача планирования пр-ва): Для изготовления n видов продукции P_j используют m видов ресурсов S_i. Обозначим: - число единиц продукции P_j, запланированной к проив-ву; 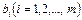- запас ресурса S_i; - число единиц ресурса S_i, затрачиваемого на изготовление единицы прод-ии P_j; - прибыль от реализации единицы продукции. Необходимо составить такой план произв-ва продукции, при к-м прибыль от ее реализации будет максимальной. ЭММ задачи об использ-ии рес-сов в общем виде: найти такой план выпуска продукции, удовлетворяющий сис-ме и условию 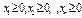, при к-м функция принимает максимальное значение. Задача составления рациона (задача о диете, о смесях): Имеется n видов корма, содержащего питательные вещ-ва (витамины) S_i. Обозначим: - число единиц корма n-го вида; 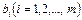- необходимый минимум содержания в рационе питательного вещ-ва S_i; - число единиц питательного вещ-ва S_iв единице корма j-го вида. Необходимо составить дневной рацион, имеющий минимальную ст-ть, в к-м содержание каждого вида питательных вещ-в было бы не менее установленного предела. ЭММ: найти такой рацион , удовлетв-щий сис-ме и усл-ю , при к-м функция принимает минимальное значение. Геометрическая интерпретация задачи и ее свойства. Графический метод решения: Множ-во точек наз-ся выпуклым, если оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки. Выпуклое замкнутое множ-во точек пространства (плоскости), имеющее конечное число угловых точек, наз-ся выпуклым многогранником (многоугольником), если оно ограниченное, и выпуклой многогранной (многоугольной) областью, если оно неограниченное. Множ-во всех точек образует n-мерное точечное (векторное) пространство. ЗЛП: (1) при условиях: ; . Множ-во реш-й нерав-ва с двумя переменными яв-ся одной из 2-х полуплоскостей, на к-е вся плоскость делится прямой , включая и эту прямую, а другая полуплоскость с той же прямой есть множ-во реш-й нерав-ва . Множ-во всех реш-й линейного неравенства с n переменными 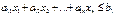яв-ся одним из полупространств, на к-е все простр-во делится плоскостью или гиперплоскостью, включая и эту плоскость (гиперплоскость). Множ-во точек, удовлетворяющих ур-ю при n=3, яв-ся плоскостью, а при n> 3 – ее обобщением в n-мерном простр-ве – гиперплоскостью. Множ-во реш-й совместной сис-мы m линейных неравенств с n переменными яв-ся выпуклым многогранником (выпуклой многогранной областью) в n-мерном пространстве. Отсюда появл-ся идея геометрического метода реш-я ЗЛП. С/с линейных ограничений ЗЛП задает в пространстве многогранное множ-во, и поскольку целевая ф-я яв-ся линейной, то она не имеет максимума (или минимума) внутри множества (т.к. 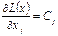не все нули). Значит экстремум L(x) достигается на границе области допустимых реш-й, т.е. в одной из вершин многогранного множества. Поэтому, если задача зависит от 2-х переменных х₁ и х₂, то ее можно решить графически. По сис-ме ограничений строится многоугольник допустимых реш-й как область пересечения прямых, задаваемых неравенствами. Линии, на к-х значение L(x) постоянно (L(x)=const или ), наз-ся линиями уровня, и что направление возрастания L(x) опр-ся вектором . Т.о. для нахождения вершины доставляющей максимальное знач-е ф-ии L(x), надо построить какую-нибудь линию уровня, н., . Затем передвигая ее параллельно самой себе в направлении вектора 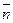, в первой встречаемой вершине многоугольника реш-й получим min L(x), а в последней пересекаемой линией уровня вершине – max L(x). Из всех линий уровня, проходящих ч/з многоугольник допустимых реш-й и имеющих с ним общие точки, выделяют две крайние с минимальным и максимальным значением целевой ф-ии. Эти линии уровня наз-ся опорными. Т.о. если область допустимых реш-й есть выпуклый многоугольник, то max или min линейной ф-ии L(x) достигаются по крайней мере в одной из вершин этого многоугольника. В общем случае область допустимых реш-й нерав-в м.б. пустой, одной точкой, выпуклым многоугольником или неограниченной выпуклой многоугольной областью. Множ-во всех планов ЗЛП выпукло. Имеет место теорема: линейная ф-я ЗЛП достигает своего экстремума в угловой точке многоугольника (многогранника) реш-й. Если линейная ф-я ЗЛП ограничена на многограннике реш-й, то: 1)сущ-ет такая угловая точка многогранника (многоугольника) реш-й, в к-й линейная ф-я ЗЛП достигает своего оптимума; 2)каждый опорный план соотв-ет угловой точке многогранника реш-й. Поэтому для реш-я ЗЛП необх-мо исслед-ть только угловые точки многогранника реш-й, т.е.только опорные планы.

49. Вычислительная схема симплексного метода решения общей задачи линейного программирования.

Построение первого опорного плана стандартной, канонической, общей задач линейного программирования: Симплекс-метод состоит из 2-х этапов: на 1-м этапе ЗЛП приводятся к базисному виду; на 2-м этапе полученное реш-е проверяется на оптимальность по критериям оптимальности. Если реш-е оптимальное, то пр-сс реш-я закончен. В противном случае поиск оптим-го реш-я продолжается до тех пор пока не найдем конечное оптим-е реш-е, либо установим, что в ЗЛП целевая ф-я не ограничена и, Þ, конечного оптим-го реш-я не сущ-ет. Симплекс-метод отличается от простого сплошного перебора тем, что на каждом повторении 2-го этапа реш-е проверяется на оптимальность. И если даже оно оказ-ся не оптимальным, то все реш-я, дающие значение целевой ф-ии хуже, чем дает данное реш-е не рассм-ся. В рез-те метод яв-ся методом направленного перебора. Доказано, что таких переборов реш-й £ 2n, где n – кол-во реш-й. При рассм-ии симплекс-метода мы исходим из того, что сис-ма ограничений имеет базисный вид. В действит-ти чаще всего ЗЛП не приведена к базисному виду. Поэтому прежде чем приступать к использ-ю симплекс-метода необх-мо каким-либо образом привести ЗЛП к базисному виду. Наиболее распространены следующие методы построения опорного реш-я: 1.Метод Гаусса (исключения переменных) для поиска неотрицательных реш-й сис-мы уравнений. Особенность этого поиска в следующем: а)приводим все свободные члены к неотрицательному виду; б)в качестве претендента в базис, выбираем переменную, к-я хотя бы в одном уравнении имеет положительный коэфф-т; в)рассм-ем отнош-я свобод-х членов к положит-м коэфф-там и среди них выбираем наименьшее. Урав-е, к-му соответ-ет наименьшее отнош-е яв-ся генеральным, и именно в этом урав-ии на оставить переменную в базисе. 2.Метод искусственного базиса. Этот метод заключ-ся в след-щем: если в урав-ии нет базисной переменной, то мы сами вводим такую искусств-ю базисную переменную . После введения в каждое урав-е искусст-х базисных переменным, сис-ма урав-й будет иметь базисный вид. Далее по симплекс-методу. В целевую функцию вводим искусственную переменную с буквой m. Если находим минимум, то –m, максимум - +m. Преобразованная т.о. задача всегда имеет оптимальное реш-е. Но если в этом оптимальном реш-ии все искусств-е переменные = 0, то реш-е яв-ся допустимым для нашей задачи (реш-е выражено не искусств-ми переменными). Значит, мы нашли базисное допустимое реш-е, проверяем на оптимальность.

Прямой и двойственный симплекс методы поиска оптимального решения задачи линейного программирования: Суть метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но не обязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за предельное число этапов (итераций). Реш-е ЗЛП вручную осущ-ся с использ-ем симплекс таблиц. Допустим 1-й этап выполнен, т.е. ЗЛП имеет базисный вид. Начинаем выполнять 2-й этап: 1. Строим 1-ю симплекс таблицу вида:

Самая верхняя строка – целевая строка, в нее записываются коэфф-ты целевой функции. Строки 1, 2, …, m – это строки функциональных ограничений. Последняя строка – Δ - дельта-строка, в нее записываем коэфф-ты Δ ₁, Δ ₂, …, Δ _n, к-е вычисляем по соответст-щим формулам. Столбец i – столбец номеров ограничений. Б – базисный столбец (сюда записываем базисные переменные). С_i – целевой столбец, записываем коэф-ты целевой ф-ии при базисных переменных. b – столбец свободных членов, в Δ -строку записываем знач-е целевой ф-ии, к-е она достигает при данном реш-ии (L₁). Х, к-е отсутствуют в базисе = 0. Тогда получим знач-е ф-ии - 1-е знач-е целевой ф-ий, а реш-е , - 1-е частное тривиальное реш-е (когда все свобод-е переменные =0, а базисные = свободным членам). Xj – столбцы переменных. 2. Вычисляем величины Dj по ф-ле или Dj=(сумма (эл-ты целевого столбца * соответ-щие эл-ты столбца Xj) – эл-т целевой строки столбца Xj). 3. На основе знач-й Δ -строки проверяем по критерию оптим-ти яв-ся ли данное реш-е оптимальным. Если реш-е оптимальное, то пр-сс реш-я закончен. В этом случае переходим к п.4. Иначе к п.5. Признак оптим-ти: Частное тривиальное реш-е яв-ся оптимальным, а знач-е целевой ф-ии, соответ-щее этому реш-ю максимально тогда, когда все Dj³ 0. Аналогично реш-е яв-ся оптимальным, а знач-е целевой ф-ии минимальным, когда все Dj£ 0. Признак неограниченности целевой ф-ии: Если при некот-й переменной Xj, Dj не удовл-ет условию оптим-ти и при этом среди коэфф-в нет положительных, то в этом случае , а , т.е. целевая ф-я не ограничена. 4. Из таблицы выписываем оптимальное реш-е ( переменным столбца Б задаем знач-я столбца b; остальные переменные полагаем =0). Оптимальное знач-е целевой ф-ии, соответ-щее данному реш-ю берем из столбца b в Δ -строке. 5.Среди Dj, к-е не удовлетворяют признаку оптимальности, рассмативаем соответ-щие столбики Xj (где j не удовл-ет оптим-ти); если Dk не удовл-ет признаку оптим-ти и среди нет положит-х, то целевая ф-я задачи не ограничена, а ЗЛП не имеет конечного реш-я. Среди величин Dj, к-е не удовл-ют оптим-ти, выбираем наибольшее по модулю. Пусть это будет Dn. 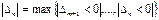. Тогда столбик Хn назовем генеральным и выделим его в таблице. Это значит, что если Хn ввести в базис, то на каждую ед-цу прироста Хn, ф-я будет измен-ся на величину (Dn*Хn). Чтобы вычислить наибольшее знач-е Хn, рассмотрим отнош-е свободных членов к положит-м коэфф-м перед Хn и среди этих отношений величин Ө выбираем минимум. Пусть это будет Ө m. 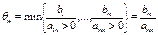. Это значит, что Хn следует оставить в базисе в уравнении с номером m, а Хm из базиса удалить. Выделяем эту строку, наз-ем ее генеральной. Тогда коэфф-т тоже наз-ся генеральным. В рез-те 1-я симплекс-таблица подготовлена для преобразования во 2-ю симпл.-табл. 6. Строим и заполняем следующую симпл.-табл. Заполняем столбец Б, причем на место Хm записываем Хn (меняем их местами). Остальные переменые ост-ся на своих местах. Вместо Cm записываем Cn. Все ост-е эл-ты основной части табл. Вычисляем по ф-ле прямоугольника в следующей последоват-ти: сначала вычисляем эл-ты генеральной строки: делим на ген-й эл-т и записываем в нов табл. с тем же номером (n). Все ост-е эл-ты заменяем на 0 в этом столбце, а на месте ген-го – 1.Все другие эл-ты вычисляем по ф-ле прямоуг-ка. , 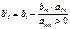. Новые знач-я эл-тов табл.=(старые знач-я эл-тов предыдущей табл. – (эл-т генер-й строки*эл-т генер-го столбца данной строки/знач-е ген-го эл-та)). Эл-ты Δ -строки тоже м. рассчитать по этим ф-м. 7. Переходим к п.3 – п.6. и повторяем их, пока не устанавливаем оптим-го реш-я или не доказ-ем, что его нет. Двойственный симплекс-метод: В этом методе предполаг-ся, что все переменные д.б. положительными. Исходной зад. строится в соответствие двойственная, к-я реш-ся симплекс-методом. Если исходная ЗЛП решена симплекс-методом, то реш-е исходной зад. содержится в последней симплекс-таблице в столбце свободных членов. Это реш-е соотв-ет переменным исх-й задачи, расположенным в базисном столбце Б. В индексной Δ -строке в столбе свободных членов нах-ся оптимальное знач-е целевой ф-ии. В столбцах переменных в Δ -строке последней симплекс-табл. содержится оптим-е реш-е двойственной задачи. При этом знач-ми переменных двойств-й задачи яв-ся Δ -оценки величины Dj. Чтобы опр-ть знач-я двойственных переменных необходимо устан-ть соответствие переменных прямой и двойственной задачи. Двойственным переменным присвоить знач-я Δ -оценок исх-х переменных прямой задачи. Н., X_n₊_i соответствует Y_i, Þ, Y_i=DX_n₊_i. X_n₊_I*Y_i=0. Базисным переменным 1-й симплекс таблицы в последней симплекс-табл. соответ-ют двойств-е перемен-е, а их значениями яв-ся соответ-щие Δ -оценки. Аналогично, не базисным переменным 1-й симпл.-табл. соотв-ют двойств-е переменные, номера к-х начин-ся после базисных переменных слева направо, значения содерж-ся в Δ -строке.

⇐ Предыдущая 18 19 20 21 222324 25 26 27 Следующая ⇒