Теоремы о геометрическом смысле неравенств, уравнений, их систем и решений. Теоремы о свойствах задачи линейного программирования (о допустимых, опорных и оптимальных решениях).
ЗЛП:  (1) при условиях:
(1) при условиях: 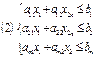 ;
; 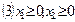 . Множ-во реш-й нерав-ва с двумя переменными
. Множ-во реш-й нерав-ва с двумя переменными  яв-ся одной из 2-х полуплоскостей, на к-е вся плоскость делится прямой
яв-ся одной из 2-х полуплоскостей, на к-е вся плоскость делится прямой  , включая и эту прямую, а другая полуплоскость с той же прямой есть множ-во реш-й нерав-ва
, включая и эту прямую, а другая полуплоскость с той же прямой есть множ-во реш-й нерав-ва  . Множ-во всех реш-й линейного неравенства с n переменными
. Множ-во всех реш-й линейного неравенства с n переменными 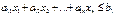 яв-ся одним из полупространств, на к-е все простр-во делится плоскостью или гиперплоскостью, включая и эту плоскость (гиперплоскость). Множ-во точек, удовлетворяющих ур-ю
яв-ся одним из полупространств, на к-е все простр-во делится плоскостью или гиперплоскостью, включая и эту плоскость (гиперплоскость). Множ-во точек, удовлетворяющих ур-ю  при n=3, яв-ся плоскостью, а при n> 3 – ее обобщением в n-мерном простр-ве – гиперплоскостью. Множ-во реш-й совместной сис-мы m линейных неравенств с n переменными яв-ся выпуклым многогранником (выпуклой многогранной областью) в n-мерном пространстве. Отсюда появл-ся идея геометрического метода реш-я ЗЛП. Сис-ма линейных ограничений ЗЛП задает в пространстве многогранное множ-во, и поскольку целевая ф-я
при n=3, яв-ся плоскостью, а при n> 3 – ее обобщением в n-мерном простр-ве – гиперплоскостью. Множ-во реш-й совместной сис-мы m линейных неравенств с n переменными яв-ся выпуклым многогранником (выпуклой многогранной областью) в n-мерном пространстве. Отсюда появл-ся идея геометрического метода реш-я ЗЛП. Сис-ма линейных ограничений ЗЛП задает в пространстве многогранное множ-во, и поскольку целевая ф-я 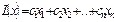 яв-ся линейной, то она не имеет максимума (или минимума) внутри множества (т.к.
яв-ся линейной, то она не имеет максимума (или минимума) внутри множества (т.к. 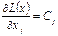 не все нули). Значит экстремум L(x) достигается на границе области допустимых реш-й, т.е. в одной из вершин многогранного множества. Поэтому, если задача зависит от 2-х переменных х1 и х2, то ее можно решить графически. По сис-ме ограничений
не все нули). Значит экстремум L(x) достигается на границе области допустимых реш-й, т.е. в одной из вершин многогранного множества. Поэтому, если задача зависит от 2-х переменных х1 и х2, то ее можно решить графически. По сис-ме ограничений 
 строится многоугольник допустимых реш-й как область пересечения прямых, задаваемых неравенствами. Линии, на к-х значение L(x) постоянно (L(x)=const или
строится многоугольник допустимых реш-й как область пересечения прямых, задаваемых неравенствами. Линии, на к-х значение L(x) постоянно (L(x)=const или  ), наз-ся линиями уровня, и что направление возрастания L(x) опр-ся вектором
), наз-ся линиями уровня, и что направление возрастания L(x) опр-ся вектором  . Т.о. для нахождения вершины доставляющей максимальное знач-е ф-ии L(x), надо построить какую-нибудь линию уровня, н.,
. Т.о. для нахождения вершины доставляющей максимальное знач-е ф-ии L(x), надо построить какую-нибудь линию уровня, н.,  . Затем передвигая ее параллельно самой себе в направлении вектора
. Затем передвигая ее параллельно самой себе в направлении вектора 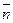 , в первой встречаемой вершине многоугольника реш-й получим min L(x), а в последней пересекаемой линией уровня вершине – max L(x). Из всех линий уровня, проходящих ч/з многоугольник допустимых реш-й и имеющих с ним общие точки, выделяют две крайние с минимальным и максимальным значением целевой ф-ии. Эти линии уровня наз-ся опорными. Т.о. если область допустимых реш-й есть выпуклый многоугольник, то max или min линейной ф-ии L(x) достигаются по крайней мере в одной из вершин этого многоугольника. В общем случае область допустимых реш-й нерав-в м.б. пустой, одной точкой, выпуклым многоугольником или неограниченной выпуклой многоугольной областью. Множ-во всех планов ЗЛП выпукло. Имеет место теорема: линейная ф-я ЗЛП достигает своего экстремума в угловой точке многоугольника (многогранника) реш-й. Если линейная ф-я ЗЛП ограничена на многограннике реш-й, то: 1)сущ-ет такая угловая точка многогранника (многоугольника) реш-й, в к-й линейная ф-я ЗЛП достигает своего оптимума; 2)каждый опорный план соотв-ет угловой точке многогранника реш-й. Поэтому для реш-я ЗЛП необх-мо исслед-ть только угловые точки многогранника реш-й, т.е.только опорные планы.
, в первой встречаемой вершине многоугольника реш-й получим min L(x), а в последней пересекаемой линией уровня вершине – max L(x). Из всех линий уровня, проходящих ч/з многоугольник допустимых реш-й и имеющих с ним общие точки, выделяют две крайние с минимальным и максимальным значением целевой ф-ии. Эти линии уровня наз-ся опорными. Т.о. если область допустимых реш-й есть выпуклый многоугольник, то max или min линейной ф-ии L(x) достигаются по крайней мере в одной из вершин этого многоугольника. В общем случае область допустимых реш-й нерав-в м.б. пустой, одной точкой, выпуклым многоугольником или неограниченной выпуклой многоугольной областью. Множ-во всех планов ЗЛП выпукло. Имеет место теорема: линейная ф-я ЗЛП достигает своего экстремума в угловой точке многоугольника (многогранника) реш-й. Если линейная ф-я ЗЛП ограничена на многограннике реш-й, то: 1)сущ-ет такая угловая точка многогранника (многоугольника) реш-й, в к-й линейная ф-я ЗЛП достигает своего оптимума; 2)каждый опорный план соотв-ет угловой точке многогранника реш-й. Поэтому для реш-я ЗЛП необх-мо исслед-ть только угловые точки многогранника реш-й, т.е.только опорные планы. 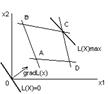
52.Задачи транспортного типа и методы их решения.
Математическая модель транспортной задачи: Транспортная ЗЛП состоит в: Имеется m пунктов пр-ва однородного груза. Объемы произв-ва в пункте с № i равны aiединиц. Груз д.б. отправлен к получателям. Потреб-ти j-го получателя равны bj ед-ц. Зная расстояние или затраты на перевозку ед-цы груза от i-го поставщика j-му получателю Cijкм (руб.), опр-ть сколько ед-ц груза следует отправить от каждого поставщика каждому получателю, чтобы в заданных условиях затраты на перевозку всего груза были минимальными. Xij – кол-во ед-ц груза от i-го поставщика j-му получателю. L(X)– общие затраты на перевозку. Целевая ф-я:  . Огранич-я:
. Огранич-я:  - огранич-е по возмож-тям поставщиков;
- огранич-е по возмож-тям поставщиков; 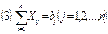 - огранич-е по получателям.
- огранич-е по получателям.  . В такой постановке модель трансп-й зад. наз-ся классической, (Канторович).
. В такой постановке модель трансп-й зад. наз-ся классической, (Канторович).
Понятия открытой и замкнутой транспортной задачи, невырожденного ее опорного решения: Если  , то такая транспортная задача наз-ся замкнутой;
, то такая транспортная задача наз-ся замкнутой;  - кол-во грузов поставщика,
- кол-во грузов поставщика,  - требуемое кол-во груза для получателя. Т.е., чтобы удовлетворить потреб-ти всех получателей, надо забрать весь груз у всех поставщиков, т.е. усл-е (2) нада записать равенством. Методы реш-я разработаны для замкнутой задачи. Если это условие не выполняется, задача наз-ся открытой: 1)
- требуемое кол-во груза для получателя. Т.е., чтобы удовлетворить потреб-ти всех получателей, надо забрать весь груз у всех поставщиков, т.е. усл-е (2) нада записать равенством. Методы реш-я разработаны для замкнутой задачи. Если это условие не выполняется, задача наз-ся открытой: 1)  Þ груза больше, чем треб-ся всем получателям, остается избыток груза, равный
Þ груза больше, чем треб-ся всем получателям, остается избыток груза, равный  . В этом случае вводят (n+1)-го получателя с объемом потребностей его =
. В этом случае вводят (n+1)-го получателя с объемом потребностей его =  , т.е. вся совокуп-ть грузов, к-я осталась на складах поставщиков идет фиктивному получателю.
, т.е. вся совокуп-ть грузов, к-я осталась на складах поставщиков идет фиктивному получателю.  . 2)
. 2)  - дефицит груза. Здесь вводят фиктивного поставщика с объемом его возможностей
- дефицит груза. Здесь вводят фиктивного поставщика с объемом его возможностей  , соответственно затраты
, соответственно затраты  . Если получатель получает какое-либо кол-во груза от фиктивного поставщика, значит он ничего не получает Þ любая задача сводится к замкнутой. Теорема Канторовича: Если свободные члены
. Если получатель получает какое-либо кол-во груза от фиктивного поставщика, значит он ничего не получает Þ любая задача сводится к замкнутой. Теорема Канторовича: Если свободные члены  ,
,  заданы в целых числах, то оптимальное реш-е получится в целых числах. При оптимизации затрат возникает необходимость учета не только затрат на перевозку, но и на пр-во груза:
заданы в целых числах, то оптимальное реш-е получится в целых числах. При оптимизации затрат возникает необходимость учета не только затрат на перевозку, но и на пр-во груза:  ,
, 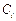 - себест-ть пр-ва ед-цы груза i-го поставщика,
- себест-ть пр-ва ед-цы груза i-го поставщика,  - перевозка.Пр-сс реш-я транспорт-й задачи включает 2 этапа: 1.Построение допустимого опорного реш-я. Это значит, что кол-во базисных переменных должно равняться кол-ву линейно-независимых уравнений. В трансп-й задаче max-е число линейно-независ-х ур-й равно m+n-1. 2.Проверка реш-я на оптимальность методом потенциалов предполагает, что загруженные клетки образуют вычеркивающуюся комбинацию. Комбинация наз-ся вычеркивающейся, если таблица содержит хотя бы одну строку или столбец с одной загруженной клеткой. Если такую строку или столбец вычеркнуть, то оставшаяся часть таблицы будет также иметь хотя бы одну строку (столбец) с 1 загруженной клеткой. Это условие необходимо для опр-я потенциала. Иначе не опр-ть потенциал вообще. Поэтому построение 1-го опорного реш-я д. удовлетворять обоим условиям: m+n-1 и вычеркивающаяся комбинация. Такое реш-е наз-ся невырожденным. Если реш-е не оптимальное, то переход к новому улучшенному опорному реш-ю. Используют метод северо-западного угла, метод Данцига, метод минимального элемента.
- перевозка.Пр-сс реш-я транспорт-й задачи включает 2 этапа: 1.Построение допустимого опорного реш-я. Это значит, что кол-во базисных переменных должно равняться кол-ву линейно-независимых уравнений. В трансп-й задаче max-е число линейно-независ-х ур-й равно m+n-1. 2.Проверка реш-я на оптимальность методом потенциалов предполагает, что загруженные клетки образуют вычеркивающуюся комбинацию. Комбинация наз-ся вычеркивающейся, если таблица содержит хотя бы одну строку или столбец с одной загруженной клеткой. Если такую строку или столбец вычеркнуть, то оставшаяся часть таблицы будет также иметь хотя бы одну строку (столбец) с 1 загруженной клеткой. Это условие необходимо для опр-я потенциала. Иначе не опр-ть потенциал вообще. Поэтому построение 1-го опорного реш-я д. удовлетворять обоим условиям: m+n-1 и вычеркивающаяся комбинация. Такое реш-е наз-ся невырожденным. Если реш-е не оптимальное, то переход к новому улучшенному опорному реш-ю. Используют метод северо-западного угла, метод Данцига, метод минимального элемента.
Методы построения первого опорного и оптимального решений: Методы вкл-ют 2 этапа: 1.Построение допустимого опорного реш-я; 2.Проверка его на оптим-ть. План состав-ся последоват-ным заполнением по одной клетке в таблице перевозок так, что каждый раз либо полностью удовлевор-ся потреб-ть одного из потребителей, либо полностью вывозится груз от некоторого поставщика. Метод северо-западного угла: на каждом шаге построения первого опорного плана заполняется верхняя левая клетка («северо-западный угол»). При таком методе заполнение таблицы начин-ся с клетки переменного х11 и заканчив-ся в клетке хmn, т.е. идет как бы по диагонали таблицы перевозок. Метод наименьшей ст-ти: Исходное опорное реш-е, построенное методом с-з угла, часто оказ-ся далеким от оптимального, т.к. при его опред-ии совершенно игнорируются величины затарат Cij. Поэтому в дальнейших расчетах тре-ся много итераций для достиж-я оптим-го плана. Число итераций м. сократить, если строить исходный план по методу «минимального элемента». Суть: на каждом шаге заполняется клетка с наименьшей величиной Cij. Если такая клетка не единственная, то лучше заполнять ту, по вертикали или горизонтали к-й встреч-ся большие Cij, а в принципе заполняется любая из них. Пусть это будет клетка (i, j). Запишем в клетку xij=min(ai, bj). Если ai< bj, то запаса пост-ка Ai исчерпаны, а потреб-ть Bj стала  . Поэтому не принимая больше во внимание i-ю строку, снова ищем клетку с наименьшей ст-тью перевозок и заполняем ее с учетом изменившихся потреб-тей. Если ai< bj из рассмотр-я исключаем j-й столбец, а запасы Ai полаг-ся равными
. Поэтому не принимая больше во внимание i-ю строку, снова ищем клетку с наименьшей ст-тью перевозок и заполняем ее с учетом изменившихся потреб-тей. Если ai< bj из рассмотр-я исключаем j-й столбец, а запасы Ai полаг-ся равными  . Пр-сс продолж-ся до тех пор пока все запасы не будут исчерпаны, а все потреб-ти – удовлетворены. Условие закрытости модели транспортной задачи означает, что среди m+n уравнений сис-мы огранич-й независимых только m+n-1, поэтому в любом базисном реш-ии этой сис-мы д.б. m+n-1 базисных переменных. Т.к. свободные переменные в таком реш-ии =0, то в трансорт-й табл. Им будут соотв-ть пустые клетки. Клетки, в к-х записаны отличные от 0 перевозки, – базисные, остальные – свободные. Базисное реш-е в условиях транспо-й зад. д. иметь m+n-1 базисных переменных. План наз-ся вырожденным, если кол-во базисных клеток в нем меньше, чем m+n-1. Если на каком-то этапе реш-я получ-ся вырожденный план, то его необх-мо пополнить, проставив в недостающем числе клеток 0 и тем самым объявив их базисными. Т.к. этим дополнит-ным клеткам будут отвечать нулевые перевозки, то общий баланс и суммарная ст-ть перевозок плана при этом не измен-ся. Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. Циклом в трансп-й табл. Наз-ся неск-ко клеток, соединенных замкнуто ломаной линией так, чтобы 2 соседние вершины ломаной были расположены либо в одной строке, либо в одном столюце. Ломаная м. иметь точки самопересеч-я, но не в клетках цикла. План наз-ся ациклическим, если его базисные клетки не содержат циклов. Доказано, что оптимальные планы яв-ся ациклическими, поэтому и первоначальный план также д. удовлетворять этому требованию. Планы полученные по методам с-з угла и наименьшей ст-ти – ациклические. Однако если план оказался вырожденным, то при его поплнении треб-е ацикличности необх-мо учитывать. Получив первый опорный план, следует проверить его на оптимальность и, если треб-ся, перейти к новому опорному плану с лучшим значением целевой ф-ии. Для этого применяют метод потенциалов. Каждому поставщику Ai и каждому потребителю Bj сопоставляют, соответст-но величины Ui и Vj – потенциалы этих пунктов. Для того, чтобы некоторый опорный план трансп-й задачи был оптимальным, необх-мо и достаточно, чтобы ему соответствовала сис-ма из (m+n) чисел Ui* и Vj*, удовлетворяющих усл-ям:
. Пр-сс продолж-ся до тех пор пока все запасы не будут исчерпаны, а все потреб-ти – удовлетворены. Условие закрытости модели транспортной задачи означает, что среди m+n уравнений сис-мы огранич-й независимых только m+n-1, поэтому в любом базисном реш-ии этой сис-мы д.б. m+n-1 базисных переменных. Т.к. свободные переменные в таком реш-ии =0, то в трансорт-й табл. Им будут соотв-ть пустые клетки. Клетки, в к-х записаны отличные от 0 перевозки, – базисные, остальные – свободные. Базисное реш-е в условиях транспо-й зад. д. иметь m+n-1 базисных переменных. План наз-ся вырожденным, если кол-во базисных клеток в нем меньше, чем m+n-1. Если на каком-то этапе реш-я получ-ся вырожденный план, то его необх-мо пополнить, проставив в недостающем числе клеток 0 и тем самым объявив их базисными. Т.к. этим дополнит-ным клеткам будут отвечать нулевые перевозки, то общий баланс и суммарная ст-ть перевозок плана при этом не измен-ся. Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. Циклом в трансп-й табл. Наз-ся неск-ко клеток, соединенных замкнуто ломаной линией так, чтобы 2 соседние вершины ломаной были расположены либо в одной строке, либо в одном столюце. Ломаная м. иметь точки самопересеч-я, но не в клетках цикла. План наз-ся ациклическим, если его базисные клетки не содержат циклов. Доказано, что оптимальные планы яв-ся ациклическими, поэтому и первоначальный план также д. удовлетворять этому требованию. Планы полученные по методам с-з угла и наименьшей ст-ти – ациклические. Однако если план оказался вырожденным, то при его поплнении треб-е ацикличности необх-мо учитывать. Получив первый опорный план, следует проверить его на оптимальность и, если треб-ся, перейти к новому опорному плану с лучшим значением целевой ф-ии. Для этого применяют метод потенциалов. Каждому поставщику Ai и каждому потребителю Bj сопоставляют, соответст-но величины Ui и Vj – потенциалы этих пунктов. Для того, чтобы некоторый опорный план трансп-й задачи был оптимальным, необх-мо и достаточно, чтобы ему соответствовала сис-ма из (m+n) чисел Ui* и Vj*, удовлетворяющих усл-ям:  (1)для
(1)для  (для занятых клеток) и
(для занятых клеток) и 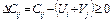 (2);
(2);  (для свободных клеток). Числа Ui* и Vj* - потенциалы соответ-но производителей и потребителей. Т.к. число неизвестных потенциалов (m+n) всегда на ед-цу больше числа уравнений (числа заполненных клеток) N= m+n-1, то выбираем строку, где есть занятая клетка и для этой строки назначаем потенциал равным 0, н., U1=0, и легко находим последовательно из уравнений (1) значения остальных потенциалов. Если число заполненных клеток N< m+n-1, то вводим дополнительно необходимое кол-во занятых клеток с нулевыми перевозками xij=0, к-е нужны для опр-я потенциалов из ур-й (1). Затем для всех свободных клеток из соотношений (2) опр-ем величину DCij и если все DCij³ 0, то получим оптимальный план перевозок, если же встречаем отрицательные DCij, то план не оптимален и его надо улучшать.
(для свободных клеток). Числа Ui* и Vj* - потенциалы соответ-но производителей и потребителей. Т.к. число неизвестных потенциалов (m+n) всегда на ед-цу больше числа уравнений (числа заполненных клеток) N= m+n-1, то выбираем строку, где есть занятая клетка и для этой строки назначаем потенциал равным 0, н., U1=0, и легко находим последовательно из уравнений (1) значения остальных потенциалов. Если число заполненных клеток N< m+n-1, то вводим дополнительно необходимое кол-во занятых клеток с нулевыми перевозками xij=0, к-е нужны для опр-я потенциалов из ур-й (1). Затем для всех свободных клеток из соотношений (2) опр-ем величину DCij и если все DCij³ 0, то получим оптимальный план перевозок, если же встречаем отрицательные DCij, то план не оптимален и его надо улучшать.
Примеры нетранспортных задач, решаемых по модели транспортной задачи: Распределительная задача. Задача о назначениях на должности: В организации имеется n должностей на к-е претендует n чел-к. Зная эфф-ть исп-я i-го специалиста на j-й должности = Cij, опр-ть какого спец-та на какую должность назначить, чтобы эффект-ть была максимальной. Искомая величина xij =1, если i-й спец-т назнач-ся на j-ю должность, xij =0, если нет. Огранич-я:  ,
,  ;
;  .
.
Математическое моделирование распределительных задач линейного программирования и способы преобразования их в модели транспортной задачи: Распределительная задача предст-ет собой специальнуюЗЛП транспортного типа, имеющую многочисленные приложения к задачам планирования, управления и проектирования. Формальная запись задачи такая же, как и у транспортной. Вместо равенств могут фигурировать и неравенства. К распредельтельным задачам сведены задачи: распределения изделий м/у препдприятиями, распр-е самолетов м/у воздушными линиями, рацион-го исп-я машинно-транспортного парка, распред-я посевной площади м/у с/х структурами и др. Постановка зад.: Имеется m видов оборуд-я, i=1, 2, …, m – номера оборуд-я, n – кол-во изделий, обрабатываемых этими станками, j=1, …, n – номера изделий. Зная фонд времени работы оборуд-я = Fi, зная Pij – производит-ть i-го станка при изготов-ии j-го изделия (часовая производит-ть), зная задание на выпуск изделий каждого вида Sj и dij – ст-ть эксплуатации одного часа i-го станка при пр-ве j-го изделия, треб-ся опр-ть ск-ко часов каждый станок д.б. загружен процессом изгот-я изделий, чтобы изготовить необх-е кол-во изделий каждого вида в пределах фонда времени работы оборуд-я при минимальных затратах (руб.), т.е. треб-ся опр-ть время tij. Сначала имеем ограничения:  (2);
(2);  (3);
(3);  (4);
(4);  (1).
(1).  (*). Предполагаем, что усл-е (*) вып-ся, т.е. если первый вид оборуд-я более производителен на первой детали, то этот вид оборуд-я будет более производителен в любом пр-ве любой детали. Подстав-ем вместо Pij в выр-е (3) выр-е (*), затем каждое огранич-е делим на bj. Из получившегося:
(*). Предполагаем, что усл-е (*) вып-ся, т.е. если первый вид оборуд-я более производителен на первой детали, то этот вид оборуд-я будет более производителен в любом пр-ве любой детали. Подстав-ем вместо Pij в выр-е (3) выр-е (*), затем каждое огранич-е делим на bj. Из получившегося:  (5);
(5); 
 (6) Þ
(6) Þ  (7). Теперь в эту сис-му вместо tij подстав-ем (5) и (6):
(7). Теперь в эту сис-му вместо tij подстав-ем (5) и (6):  (3’). Далее в сис-му (2) подставляем выр-е (7), затем умножаем обе части ограничений на a, получаем:
(3’). Далее в сис-му (2) подставляем выр-е (7), затем умножаем обе части ограничений на a, получаем:  (2’).
(2’).  (4’)
(4’)  . В целевую ф-ю вместо tij подст-ем выр-е (7), Þ,
. В целевую ф-ю вместо tij подст-ем выр-е (7), Þ,  (8). (8) подст-ем в целевую ф-ю, Þ, (1’), Þ, получаем трансп-ю зад. (1’) – (4’). Если усл-е (*) не вып-ся, то вводится поняти эталонного оборуд-я, станка. Тогда
(8). (8) подст-ем в целевую ф-ю, Þ, (1’), Þ, получаем трансп-ю зад. (1’) – (4’). Если усл-е (*) не вып-ся, то вводится поняти эталонного оборуд-я, станка. Тогда 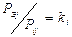 - коэфф-т пропорц-ти i-го станка, Þ,
- коэфф-т пропорц-ти i-го станка, Þ,  .
.  (6);
(6);  Þ
Þ  (7);
(7);  ;
;  (8). Получаем трансп-ю зад. Алгоритм преобразования: 1.В каждой строке таблицы производит-тей Pij опр-ем наибольший общий делитель (НОД) ai и выносим его за пределы таблицы. 2.Аналогично для каждого столбца этой таблицы опр-ем НОД=bj, его тоже выносим за пределы таблицы. Если не получается так, что все Pij имеют общий множитель, то считаем приблизительно. Вычисляем по ф-ле (5) величины bj и интерпретируем их как потреб-ть машинного времени j-го получателя. По ф-ле (6) вычисляем ai и интерпретируем как возможности i-го поставщика машинного времени. По ф-ле (8) вычисляем Cij как затраты на передачу машинного времени от i-го поставщика j-му получателю. В качестве искомых величин принимаем xij как кол-во времени, к-е i-й поставщик поставляет j-му получателю. L(x) выражает общие затраты на передачу всего времени от всех поставщиков ко всем получателям. 3.Теперь строим обычную трансп-ю задачу. 4.По оптим-му реш-ю трансп-й зад. вычисляем искомые величины tij по ф-ле (7).
(8). Получаем трансп-ю зад. Алгоритм преобразования: 1.В каждой строке таблицы производит-тей Pij опр-ем наибольший общий делитель (НОД) ai и выносим его за пределы таблицы. 2.Аналогично для каждого столбца этой таблицы опр-ем НОД=bj, его тоже выносим за пределы таблицы. Если не получается так, что все Pij имеют общий множитель, то считаем приблизительно. Вычисляем по ф-ле (5) величины bj и интерпретируем их как потреб-ть машинного времени j-го получателя. По ф-ле (6) вычисляем ai и интерпретируем как возможности i-го поставщика машинного времени. По ф-ле (8) вычисляем Cij как затраты на передачу машинного времени от i-го поставщика j-му получателю. В качестве искомых величин принимаем xij как кол-во времени, к-е i-й поставщик поставляет j-му получателю. L(x) выражает общие затраты на передачу всего времени от всех поставщиков ко всем получателям. 3.Теперь строим обычную трансп-ю задачу. 4.По оптим-му реш-ю трансп-й зад. вычисляем искомые величины tij по ф-ле (7).
Примеры формулирования организационно-технологических задач в форме математической модели распределительной задачи: В механической мастерской имеется 3 группы взаимозаменяемого оборуд-я, на к-м изготавлив-ся 4 вида деталей. Фонд времени оборуд-я Fi, задание на пр-во деталей Sj. Производит-ти оборуд-я по изгот-ю - Pij и затраты в рублях одного часа работы оборуд-я на пр-ве каждой детали известны. Необх-мо опр-ть, ск-ко часов каждый станок д. отработать на пр-ве каждой детали, ск-ко деталей он д. изготовить, чтобы вып-ть задание по выпуску деталей в пределах фонда времени при минимуме затрат.
Популярное:

