
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Термодинамика гальванического элемента
Электрохимический метод широко применяется при исследовании термодинамических свойств различных химических процессов, на основе которых можно построить равновесные электрохимические цепи. Кроме того, этот метод более прост, а также позволяет изучать процессы при высоких температурах, что свидетельствует о ряде преимуществ перед другими. Измерение ЭДС позволяет определить такие термодинамические характеристики, как изобарный потенциал (DG), тепловой эффект реакции (DН), изменение энтропии (DS) и константу равновесия (Кр) окислительно-восстановительной реакции, которая протекает в гальваническом элементе.
Определение термодинамических характеристик Токообразующей реакции
Токообразующей реакцией называется та окислительно-восстановительная реакция, которая самопроизвольно протекает в гальваническом элементе. Например, в элементе Даниэля –Якоби:
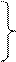 Zn0 ® Zn2+ + 2 Zn0 ® Zn2+ + 2 
Zn0+ + Cu2+ ® Zn2+ + Cu0 токообразующая реакция C помощью электрохимического метода могут быть рассчитаны следующие термодинамические характеристики: а) Расчет изменения потенциала (DG). Из раздела термодинамики известно, что DG = –Wmax Для электрохимической цепи максимальную электрическую работу характеризует величина W = zFE, где z – количество электронов, принимающих участие в реакции; F – число Фарадея. Следовательно, DG = zFE (7.78) Это уравнение служит основой расчета DG различных химических реакций. Часто электрохимический метод определения изобарного потенциала имеет существенные преимущества передтермохимическим методом. б) Расчет константы равновесия (Кр). При стандартных условиях DG0 = z F E0 Из термодинамики также известно, что
Следовательно, Величина Кр характеризует полноту протекания химической реакции и вычисляется из уравнения: в) Расчет изменения энтропии (DS). Из раздела термодинамики известно, что
Используя уравнение (7.6.1) DG = – z FE, находим, что Следовательно, где изменяется ЭДС при изменении температуры на 1 градус. Для нахождения ЭДС гальванической цепи зависит от температуры. Для одних цепей она увеличивается с повышением температуры, а для других – уменьшается. Изучение температурной зависимости гальванической цепи представляет большой интерес. Точное измерение самой ЭДС и ее температурного коэффициента г) Расчет теплового эффекта реакции (DH). К гальванической цепи, как и ко всякой химической и электрохимической системе, находящейся при постоянном давлении применимы все основные уравнения химической термодинамики, в том числе и уравнения Гиббса – Гельмгольца:
где DH – изменение энтальпии в ходе химической реакции. Используя уравнения (7.6.1) и (7.6.3), получим –z FE = DH – Tz F или DH = – z F Следовательно, измерив ЭДС и взяв ее производную Проведем анализ: Если все члены уравнения Гиббса – Гельмгольца разделить на zF и поменять знаки, то с учетом формулы Е = – получим следующее выражение: Е = – Как уже указывалось ранее
то Таким образом, температурный коэффициент характеризует и изменение энтропии (DS) в ходе соответствующей химической реакции, а величина zFT . определяет тепловой эффект при обратимом протекании химической реакции в электрохимической системе. С другой стороны, DH характеризует тепловой эффект химической реакции при ее необратимом протекании в условиях постоянного давления. Будем рассматривать только самопроизвольно протекающие химические реакции, для которых Е > 0. Такого вида электрохимические реакции протекают в гальваничес-ких элементах. На опыте наблюдаются все три случая зависимости ЭДС от температуры 1. 2. 3. Рассмотрим эти случаи с точки зрения соотношения электрической энергии и энергии химической реакции. Если то z FE = DH, т.е. вся энергия, выделяющаяся при химической реакции, превращается в электрическую работу (W = zFE). Если то z F E = DH – z F E . т. е. только часть энергии, выделяющейся при химической реакции, превращается в электрическую работу, а другая часть (q) выделяется в виде теплоты и элемент нагревается. Наиболее интересен случай, когда Тогда z F E = DH + z F E . т.е. электрическая работа больше энергии, выделяющейся при химической реакции на величину (q). Дополнительная работа получается за счет теплоты, которую элемент отбирает от окружающей среды. Если система изолирована, то элемент охлаждается. Таким образом, не имея разности температур, можно получить превращение теплоты в работу, т.е. протекает отрицательный процесс с уменьшением энтропии. Электрохимические цепи, отвечающие таким необычным условиям, действительно можно реализовать. Пример 1. Рассмотрим следующую цепь: (–) Ag, AgCl½ HCl½ Hg2Cl2, Hg½ Ag (+), в которой осуществляется реакция 1/2Hg2Cl2 + Ag ® Hg + AgCl ЭДС этой цепи при 250 С Е = 0, 0465, а Решение: По формуле (6.4) найдем изменения энтальпии
» 5, 3 . 103 Дж/моль = 5, 3 кДж/моль Положительное значение DH указывает на эндотермический характер приведенной реакции. Аналогичные закономерности наблюдаются за счет возрастания энтропии системы. Пример 2. Рассчитать значения Pb, PbCl2½ HCl½ Hg2Cl2, Hg, если ее ЭДС равен 0, 536 В, а температурный коэффициент равен 0, 45 . 10 –4 В/к. Написать уравнение реакции протекающий в цепи. Решение: Электрохимическая цепь состоит из двух электродов II рода Cl–½ PbCl2, Pb и Cl–½ Hg2Cl2, Hg
реакции: Hg2Cl2 + 2 токообразующая реакция: Pb + Hg2Cl2 PbCl2 + 2Hg Используем уравнения (7.78), (7.80) и (7.81) для нахождения 1) 3) DНТ = = –94, 18 кДж/моль 2) DST = отрицательное значение ( Весьма интересным является вопрос о коэффициенте полезного действия (КПД) при работе элемента (h). Если просто сжигать топливо, а затем превращать часть теплоты в работу тепловой машины, то достигается небольшой КПД (до 0, 3-0, 4). Если же осуществлять химическую реакцию окисления топлива в электрическом элементе, то можно получить значительно больший КПД. Теоретически КПД может быть больше единицы в элементах, у которых температурный коэффициент больше нуля, т.е. если Таким образом, по экспериментальным значениям ЭДС (Е) можно не только определять важнейшие термодинамические характеристики токообразующей реакции, которые будут такими же и в том случае, если данная реакция протекает не в элементе, но и можно решить обратную задачу, т.е. по термодинамическим данным рассчитать ЭДС (Е) и температурный коэффициент. Заметим также, что зная DG0 = – z FE0, затем по известному значению Е0 можно вычислить ЭДС для любых концентраций ионов в растворе. Например, для реакции а1А1 + а2А2 = в1В1 + в2В2 Е = Е0 – Так, многие стандартные потенциалы металлов, которые не могут быть определены экспериментально, вычислены на основании термодинамичес-ких данных. Например, для щелочных и щелочноземельных металлов, которые бурно реагируют с водой, для алюминия и магния, которые легко покрываются пленкой и т.д. Популярное:
|
Последнее изменение этой страницы: 2016-08-24; Просмотров: 3864; Нарушение авторского права страницы