
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Уравнение теплопроводности и его формы
Уравнение теплопроводности получено феноменологическим путем. Феноменология – наука, которая описывает явления с помощью математического аппарата. Чаще всего для этого описания применяются балансные соотношения, такие как уравнение сохранения энергии, импульса, массы, уравнение состояния. Уравнение теплопроводности можно считать частным случаем уравнения энергии. В рамках феноменологической теории рассматривается элементарный объем линейным размером dх, в который поступает количество теплоты Q0, а выходит – Q1. В этом объеме происходит поглощение части теплоты. За это отвечает удельная теплоемкость с и плотность ρ. Количество теплоты, которое может быть передано, зависит от коэффициента теплопроводности
Это – уравнение теплопроводности в ортотропном теле (коэффициенты теплопроводности различны для трех главных осей: x, y, и z). Первый член отвечает за аккумуляцию (накопление) теплоты. Оператор с – удельная теплоемкость
С=сρ – объемная теплоемкость, В правой части этого уравнения первые три составляющие характеризуют тепловые потоки, которые распределяются по трем главным осям. Уравнение (1) нелинейное, так как коэффициенты, стоящие перед операторами Последний член уравнения В инженерных приложениях большое распространение получили одномерные варианты уравнения теплопроводности. Классическая теория теплопроводности хорошо разработана для линеаризованных (линейных) уравнений. Так, уравнение (1) в одномерном и линейном случае можно записать:
Как видно, пропала зависимость коэффициента от температуры. Это уравнение с постоянными коэффициентами. Для решения применяются классические методы: преобразования Фурье, Лапласа, разделения переменных. Однако, на практике, особенно при анализе высокотемпературных процессов, считать коэффициенты постоянными нельзя. С решением нелинейных уравнений теплопроводности успешно справляются численные методы: метод конечных элементов, граничных элементов, метод конечных разностей. Для линейных уравнений получены замкнутые зависимости, которые именуются формулами. Для нестационарных многомерных процессов эти формулы имеют громоздкий вид. К тому же, для получения конкретных численных результатов необходимо использовать ЭВМ. По этой же причине в настоящее время предпочтение отдается численным методам, а аналитические зависимости используются для проверки численных решений. В ходе такой проверки нелинейная модель искусственно загрубляется. Вместо температурных зависимостей коэффициентов вводятся их постоянные значения. Частным случаем уравнения (2) является случай достижения линейного стационарного температурного состояния. Тогда:
Если в теле отсутствую внутренние источники теплоты, то:
Для цилиндрической и сферической стенки уравнение (2) может быть записано следующим образом:
Не трудно увидеть, что отличие от уравнения (2) выражается вторыми членами в скобках. В случаях, когда толщина стенки В тонкостенных телах перепад температур по толщине мал; можно считать, что температура изменяется только во времени.
Рис. 2.2
Таким образом, температура на фронтальной поверхности Tw1 равна температуре на тыльной поверхности Tw2: Tw1=Tw2=f(
Конкретная структура Одним из законов, регулирующих отвод (подвод) теплоты, является закон Стефана-Больцмана: где В случае одностороннего подвода теплоты и двустороннего отвода:
В частном случае нет изменения температуры
В случае конвективного нагрева
Температура, которая определяется по этой формуле и предыдущей, называется равновесной (равенство между количеством подведенной и отведенной теплоты).
2.1.2. Условия однозначности для решения уравнения
Для однозначного решения уравнения теплопроводности к нему необходимо присоединить начальные, граничные, геометрические и физические условия. Начальное условие: τ =0, Т = Т0; Т0(x, y, z) – если начальное температурное поле неоднородно: в разных точках различная температура. Граничные условия в теплофизике принято делить на условия первого, второго, третьего и четвертого рода. Граничные условия 1 рода x=0, Т=Т1(2)(τ ); В частном случае это постоянная температура, не изменяющаяся во времени. Температура может быть измерена контактными или бесконтактными методами. Либо эта температура может быть увязана с некоторыми хорошо контролируемыми явлениями, такими как: испарение, плавление. Для измерения температуры используются термокраски. Граничные условия 2 рода х=0(l);

где
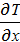 – градиент температуры в теле; – градиент температуры в теле;
Рис. 2.3
Граничные условия 3 рода Заключаются в задании коэффициента теплоотдачи.
где f – «flow» - поток; w – «wall» - стена. Таким образом,
Граничные условия 4 рода Задание равенства тепловых потоков на границе двух тел
Иногда такую форму записи именуют условием идеального теплового контакта.
На границе двух тел нет скачка температур.
Рис. 2.4
В некоторых случаях граничное условие 4 рода может быть усложнено, в частности при возникновении физико-химических превращений на границе, при возникновении тонких нерегулярных прослоек. В этих случаях в уравнение добавляются дополнительные члены, описывающие возникающие физические явления.
Популярное:
|
Последнее изменение этой страницы: 2016-08-24; Просмотров: 644; Нарушение авторского права страницы