Прочих, неучтенных факторов.
Этот показатель вычисляется по формуле
 , (5.2.1.) , (5.2.1.)
где yi – индивидуальные значения результативного признака;
 – общая средняя значений результативного признака; – общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя 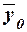 вычисляется как средняя арифметическая простая по всем единицам совокупности: вычисляется как средняя арифметическая простая по всем единицам совокупности:
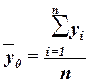 (5.2.2.) (5.2.2.)
или как средняя взвешенная по частоте групп интервального ряда:
 (5.2.3.) (5.2.3.)
Для вычисления 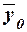 удобно использовать формулу (5.2.2.), т.к. в табл. 3.2.3. (графы 6 и 3 итоговой строки) имеются значения числителя и знаменателя формулы. удобно использовать формулу (5.2.2.), т.к. в табл. 3.2.3. (графы 6 и 3 итоговой строки) имеются значения числителя и знаменателя формулы.
Таблица 5.2.1.
| Аналитическая группировка зависимости кредитных вложений и прибыли банков
| | Номер
группы
| Группы банков по величине кредитных вложений, млн.руб.
| Число банков,
f
| Прибыль банка, млн. руб.
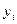
| | | Всего
| В среднем по группе на 1 банк 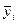
| | |
|
|
|
| гр.5=гр.4: гр.3
| | |
| 375, 00 - 459, 00
|
| 684, 000
| ?
| | |
| 459, 00 - 543, 00
|
| 1002, 000
| ?
| | |
| 543, 00 - 627, 00
|
| 2508, 000
| ?
| | |
| 627, 00 - 711, 00
|
| 1772, 000
| ?
| | |
| 711, 00 - 795, 00
|
| 884, 000
| ?
| | |
| итого
|
| 6850, 00
| ?
| |
Расчет  по формуле (5.2.3): по формуле (5.2.3):
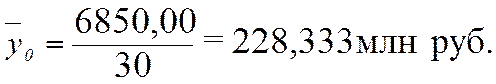
Для расчета общей дисперсии 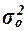 применяется вспомогательная таблица 5.2.1. применяется вспомогательная таблица 5.2.1.
Таблица 5.2.2.
Вспомогательная таблица для расчета общей дисперсии
| Номер
банка
п/п
| Прибыль, млн. руб.
   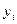
| 
| 
| |
|
| гр.3=гр.2-228.333
| гр.4=гр.3*гр.3
| |
|
| 256-228, 333=
27, 667
| 27, 6672= 765, 463
| |
|
| -60, 333
| 3640, 071
| |
|
| 23, 667
| 560, 127
| |
|
| -7, 333
| 53, 773
| |
|
| -18, 333
| 336, 099
| |
|
| 49, 667
| 2466, 811
| |
|
| -14, 333
| 205, 435
| |
|
| -59, 333
| 3520, 405
| |
|
| 59, 667
| 3560, 151
| |
|
| -15, 333
| 235, 101
| |
|
| -78, 333
| 6136, 059
| |
|
| -20, 333
| 413, 431
| |
|
| -10, 333
| 106, 771
| |
|
| -1, 333
| 1, 777
| |
|
| 9, 667
| 93, 451
| |
|
| 25, 667
| 658, 795
| |
|
| 22, 667
| 513, 793
| |
|
| 64, 667
| 4181, 821
| |
|
| -70, 333
| 4946, 731
| |
|
| -33, 333
| 1111, 089
| |
|
| 8, 667
| 75, 117
| |
|
| 10, 667
| 113, 785
| |
|
| -37, 333
| 1393, 753
| |
|
| 7, 667
| 58, 783
| |
|
| -13, 333
| 177, 769
| |
|
| 74, 667
| 5575, 161
| |
|
| -0, 333
| 0, 111
| |
|
| 1, 667
| 2, 779
| |
|
| 36, 667
| 1344, 469
| |
|
| 16, 667
| 277, 789
| | Итого:
|
| 0, 01
| 42526, 667
|
Расчет общей дисперсии по формуле (5.2.1.):
 (безразмерна!!! ) (безразмерна!!! )
Межгрупповая дисперсия  измеряет систематическую вариацию результативного признака (У), (Прибыли банка), обусловленную влиянием только признака-фактора Х (Объем кредитных вложений) (по которому произведена группировка). измеряет систематическую вариацию результативного признака (У), (Прибыли банка), обусловленную влиянием только признака-фактора Х (Объем кредитных вложений) (по которому произведена группировка).
| Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних  от общей средней от общей средней  . .
Для нашей задачи: межгрупповая дисперсия  отражает вариацию прибыли под влиянием только: отражает вариацию прибыли под влиянием только:
1)объема кредитных вложений (наш факторный признак - х);
Показатель  вычисляется по формуле вычисляется по формуле
 , (5.2.5.) , (5.2.5.)
где 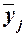 –групповые средние, –групповые средние,
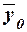 – общая средняя, – общая средняя,
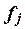 –число единиц в j-ой группе, –число единиц в j-ой группе,
k – число групп.
Для расчета межгрупповой дисперсии  строится вспомогательная таблица 5.2.2. При этом используются групповые средние значения строится вспомогательная таблица 5.2.2. При этом используются групповые средние значения 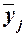 из табл. 5.2.3. (графа 7). из табл. 5.2.3. (графа 7).
Таблица 5.2.3.
Вспомогательная таблица для расчета межгрупповой дисперсии
Группы банков по размеру кредитных вложений,
млн. руб. 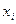
| Число банков,
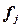
| Прибыль банков всего, млн. руб.
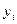
| Средняя прибыль банков по группе,  млн. Руб.
млн. Руб.
| 
| 
| 
| |
|
|
|
| гр.5=гр.4-228, 333
| гр6=
гр5*гр5
| гр7=
гр6*гр2
| | 375, 00 - 459, 00
|
|
| 171, 000
|
?
|
?
|
?
| | 459, 00 - 543, 00
|
|
| 200, 400
|
?
|
?
|
?
| | 543, 00 - 627, 00
|
|
| 228, 000
|
?
|
?
|
?
| | 627, 00 - 711, 00
|
|
| 253, 143
|
?
|
?
|
?
| | 711, 00 - 795, 00
|
|
| 294, 667
|
?
|
?
|
?
| | итого
|
|
| 228, 333
|
|
|
?
| | | | | | | | | |
 Расчет межгрупповой дисперсии Расчет межгрупповой дисперсии  по формуле (5.2.5.): по формуле (5.2.5.):
Исходя из правила сложений дисперсий вычисляются показатели, оценивающие силу и тесноту связи между факторным и результативным признаком
Эмпирический коэффициент детерминации  оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов).
| Для нашей задачи: насколько вариация прибыли (y) объясняется вариацией кредитных вложений (х)
Показатель  (этта квадрат) рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле (этта квадрат) рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
 , (5.2.6.) , (5.2.6.)
где 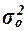 – общая дисперсия признака Y, – общая дисперсия признака Y,
 – межгрупповая (факторная) дисперсия признака Y. – межгрупповая (факторная) дисперсия признака Y.
Значения эмпирического коэффициента детерминации  изменяются в пределах изменяются в пределах  . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство  = 0, а при наличии функциональной связи между ними - равенство = 0, а при наличии функциональной связи между ними - равенство  = 1. Чем ближе его значение к 1, тем связь теснее. = 1. Чем ближе его значение к 1, тем связь теснее.
Расчет эмпирического коэффициента детерминации  по формуле (5.2.6.): по формуле (5.2.6.):
 или _____? % или _____? %
Вывод. ______? % вариации суммы прибыли банков обусловлено вариацией объема кредитных вложений, а ______? % – влиянием прочих, неучтенных в данном исследовании факторов.
Эмпирическое корреляционное отношение  оценивает тесноту связи между факторным и результативным признаком оценивает тесноту связи между факторным и результативным признаком
| Для нашей задачи: теснота связи между объемом кредитных вложений и суммой прибыли банков
Эмпирическое корреляционное отношение  (этта) вычисляется по формуле (этта) вычисляется по формуле
 (5.2.7.) (5.2.7.)
Значение показателя изменяются в пределах  . Чем ближе значение . Чем ближе значение  к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе  служит шкала Чеддока (табл. 14): служит шкала Чеддока (табл. 14):
Таблица 5.2.4.
Шкала Чеддока
| h
| 0, 1 – 0, 3
| 0, 3 – 0, 5
| 0, 5 – 0, 7
| 0, 7 – 0, 9
| 0, 9 – 0, 99
| | Характеристика
силы связи
| Слабая
| Умеренная
| Заметная
| Тесная
| Весьма тесная
| Расчет эмпирического корреляционного отношения  по формуле (5.2.7.): по формуле (5.2.7.):
 или _______? % или _______? %
Вывод. Согласно шкале Чэддока связь между объемом кредитных вложений и суммой прибыли банков является _______________________? .
Правило сложения дисперсий:
Правило сложения дисперсий: общая дисперсия признака (σ 2) равна сумме межгрупповой дисперсии (δ 2) и средней из внутригрупповых дисперсий (  ) )
σ 2 = δ 2 +  (5.2.8.) (5.2.8.)
Правило сложения дисперсий имеет практическое значение при определении одной из дисперсий, если известны две другие. Например, зная общую и межгрупповую (факторную) дисперсии, можно определить среднюю дисперсию из внутригрупповых, характеризующую влияние неучтённых факторов.
Рассчитаем внутригрупповую дисперсию и среднюю из внутригрупповых для сквозной задачи:
Внутригрупповые дисперсии (  ) характеризуют вариацию результативного признака под влиянием прочих, неучтенных факторов, рассчитываются для отдельных групп. ) характеризуют вариацию результативного признака под влиянием прочих, неучтенных факторов, рассчитываются для отдельных групп.
Для нашей задачи: средняя из внутригрупповых дисперсий отражает вариацию прибыли под влиянием
Популярное:
|

