Определение отношения теплоемкостей газов методом адиабатического расширения
Принадлежности: стеклянный баллон, закрытый пробкой, манометр, насос.
Краткая теория. Под теплоемкостью тела понимают физическую величину, численно равную количеству теплоты, которое необходимо подвести к телу, чтобы повысить его температуру на один градус: 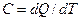 . Теплоемкость газов зависит от условий, при которых производится их нагревание. Наибольший интерес представляет теплоемкость газа для случаев, когда нагревание происходит при постоянном объеме (
. Теплоемкость газов зависит от условий, при которых производится их нагревание. Наибольший интерес представляет теплоемкость газа для случаев, когда нагревание происходит при постоянном объеме ( 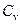 ) или при постоянном давлении (
) или при постоянном давлении ( 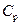 ).
).
Непосредственное измерение теплоемкости газа при постоянном объеме сопряжено со значительными трудностями. Поэтому для вычисления 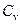 можно использовать значение
можно использовать значение 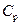 и отношение
и отношение 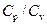 , которое, например, в случае воздуха может быть определено экспериментально достаточно простым способом. Найти отношение
, которое, например, в случае воздуха может быть определено экспериментально достаточно простым способом. Найти отношение 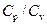 можно, воспользовавшись уравнением состояния газа и первым началом термодинамики.
можно, воспользовавшись уравнением состояния газа и первым началом термодинамики.
Состояние газа может быть охарактеризовано тремя параметрами: давлением 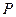 , объемом
, объемом 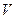 и температурой
и температурой 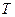 . Уравнение, связывающее эти величины, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева–Клапейрона, которое для одного моля газа имеет вид
. Уравнение, связывающее эти величины, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева–Клапейрона, которое для одного моля газа имеет вид
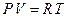 , ,
| (1)
|
где 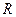 – универсальная газовая постоянная.
– универсальная газовая постоянная.
Первое начало термодинамики говорит о том, что количество теплоты 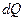 , переданное системе, затрачивается на увеличение ее внутренней энергии
, переданное системе, затрачивается на увеличение ее внутренней энергии 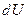 и на работу
и на работу 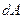 , совершаемую системой против внешних сил:
, совершаемую системой против внешних сил:
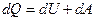 . .
| (2)
|
Из определения теплоёмкости следует:
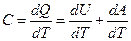 . .
| (3)
|
Из (3) видно, что в зависимости от способов нагревания газа теплоёмкость может иметь различные значения, поскольку одному и тому же значению 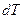 могут соответствовать разные значения
могут соответствовать разные значения 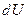 и
и 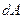 . Элементарная работа газа
. Элементарная работа газа 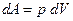 . При изохорическом процессе, когда объем сохраняется постоянным,
. При изохорическом процессе, когда объем сохраняется постоянным, 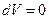 , а значит и
, а значит и 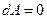 ; при этом все подводимое к газу тепло идет на увеличение внутренней энергии газа. Из (3) следует, что при постоянном объеме молярная теплоемкость газа равна:
; при этом все подводимое к газу тепло идет на увеличение внутренней энергии газа. Из (3) следует, что при постоянном объеме молярная теплоемкость газа равна:
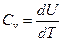 . .
| (4)
|
При изобарическом процессе 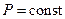 уравнение (3) имеет вид:
уравнение (3) имеет вид:
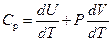 . .
| (5)
|
Уравнение состояния газа (1) можно переписать:
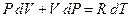 . .
| (6)
|
В случае 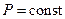 изменение давления
изменение давления 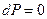 , тогда
, тогда 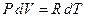 . Подставляя последнее равенство в (5) и заменяя в нем
. Подставляя последнее равенство в (5) и заменяя в нем 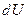 на
на 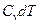 , окончательно получим:
, окончательно получим:
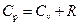 . .
| (7)
|
Это соотношение носит имя Майера.
Отношение теплоемкостей газа 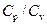 входит в уравнение Пуассона, описывающее адиабатический процесс. Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой. К адиабатическим можно отнести все быстро протекающие процессы. Например, адиабатическим можно считать процесс распространения звуковых (ультразвуковых) волн в упругой среде.
входит в уравнение Пуассона, описывающее адиабатический процесс. Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой. К адиабатическим можно отнести все быстро протекающие процессы. Например, адиабатическим можно считать процесс распространения звуковых (ультразвуковых) волн в упругой среде.
Чтобы получить уравнение адиабатического процесса, запишем первое начало термодинамики в отсутствие теплообмена 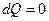 :
:
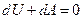 и и 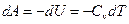 . .
|
|
Видно, что при адиабатическом процессе расширения или сжатия работа совершается газом за счет изменения запаса внутренней энергии. Поскольку 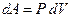 , можно записать
, можно записать
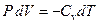 . .
| (8)
|
Разделив (6) на (8) и учитывая уравнение (7), получим:
или
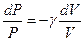 , ,
| (9)
|
где 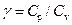 .
.
Интегрируя и потенцируя выражение (9), получим уравнение Пуассона:
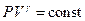 . .
| (10)
|
Определение величины 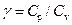 можно производить различными методами (в частности, акустическими). В данной работе для определения
можно производить различными методами (в частности, акустическими). В данной работе для определения 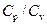 предлагается метод, использующий процесс адиабатического расширения воздуха. Этот метод не обладает высокой точностью и дает, как правило, заниженные значения, но он прост в реализации.
предлагается метод, использующий процесс адиабатического расширения воздуха. Этот метод не обладает высокой точностью и дает, как правило, заниженные значения, но он прост в реализации.
Экспериментальная установка состоит из стеклянного баллона большой емкости, который при помощи крана 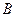 может соединяться с насосом или атмосферой (рис. 1). Разность между давлением воздуха в баллоне
может соединяться с насосом или атмосферой (рис. 1). Разность между давлением воздуха в баллоне 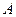 и атмосферным давлением
и атмосферным давлением 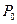 измеряется при помощи открытого манометра
измеряется при помощи открытого манометра 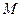 , одно из колен которого соединяется с сосудом
, одно из колен которого соединяется с сосудом 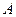 . В качестве манометрической жидкости используется подкрашенная вода.
. В качестве манометрической жидкости используется подкрашенная вода.
Соединив при помощи крана и резинового шланга баллон 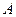 с насосом, в баллон нагнетают воздух. Когда разность уровней жидкости в манометре станет равной 10–15 см, кран закрывают. Нагнетание воздуха производится быстро, поэтому процесс его сжатия близок адиабатическому. Это приводит к повышению температуры воздуха в баллоне. Для установления равновесного состояния требуется время, в течение которого происходит теплообмен воздуха в баллоне с окружающей средой; при этом давление газа в сосуде изменяется (понижается). Понижение давления происходит до тех пор, пока в баллоне не установится постоянная температура, равная комнатной.
с насосом, в баллон нагнетают воздух. Когда разность уровней жидкости в манометре станет равной 10–15 см, кран закрывают. Нагнетание воздуха производится быстро, поэтому процесс его сжатия близок адиабатическому. Это приводит к повышению температуры воздуха в баллоне. Для установления равновесного состояния требуется время, в течение которого происходит теплообмен воздуха в баллоне с окружающей средой; при этом давление газа в сосуде изменяется (понижается). Понижение давления происходит до тех пор, пока в баллоне не установится постоянная температура, равная комнатной.
Пусть 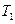 – абсолютная температура воздуха в баллоне после установления температурного равновесия,
– абсолютная температура воздуха в баллоне после установления температурного равновесия, 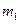 – его масса,
– его масса, 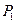 – давление,
– давление, 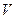 – объем, равный объему баллона. Очевидно, что
– объем, равный объему баллона. Очевидно, что 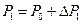 , где
, где 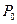 – атмосферное давление. Разность
– атмосферное давление. Разность 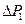 между давлением в баллоне и атмосферным измеряется в мм водяного столба и численно равна разности уровней жидкости в коленах манометра, т.е.
между давлением в баллоне и атмосферным измеряется в мм водяного столба и численно равна разности уровней жидкости в коленах манометра, т.е. 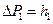 . Давления
. Давления 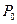 и
и 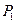 должны быть измерены в одних и тех же единицах.
должны быть измерены в одних и тех же единицах.
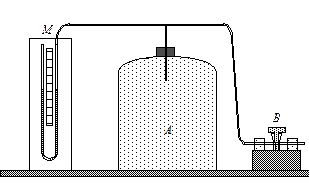 Рис. 1
Рис. 1
|
Измерив 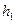 , открывают кран
, открывают кран 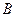 (просто достают его из гнезда), позволяя воздуху выйти из баллона
(просто достают его из гнезда), позволяя воздуху выйти из баллона 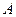 , затем возвращают в прежнее положение. При этом необходимо обеспечить условия, когда процесс расширения воздуха можно считать адиабатическим, а его конечное давление – атмосферным. Поскольку точно определить момент, когда давление расширяющегося воздуха станет равным атмосферному, трудно (т.к. после открытия крана появляются значительные колебания давления газа в баллоне), следует закрыть кран сразу после прекращения звука, возникающего при выходе воздуха через отверстие крана.
, затем возвращают в прежнее положение. При этом необходимо обеспечить условия, когда процесс расширения воздуха можно считать адиабатическим, а его конечное давление – атмосферным. Поскольку точно определить момент, когда давление расширяющегося воздуха станет равным атмосферному, трудно (т.к. после открытия крана появляются значительные колебания давления газа в баллоне), следует закрыть кран сразу после прекращения звука, возникающего при выходе воздуха через отверстие крана.
При адиабатическом расширении воздуха (в ходе которого давление понижается до уровня 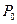 ) его внутренняя энергия уменьшается и, следовательно, понижается температура (значение
) его внутренняя энергия уменьшается и, следовательно, понижается температура (значение 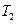 ). Так как при расширении часть воздуха из баллона выйдет, масса оставшегося в баллоне воздуха (обозначим ее
). Так как при расширении часть воздуха из баллона выйдет, масса оставшегося в баллоне воздуха (обозначим ее 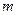 ) при том же объеме
) при том же объеме 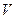 будет меньше массы
будет меньше массы 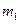 .
.
В закрытом баллоне 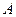 воздух начинает нагреваться вследствие теплообмена с окружающей средой; давление его увеличивается, о чем можно судить по манометру: перепад уровней жидкости увеличивается.
воздух начинает нагреваться вследствие теплообмена с окружающей средой; давление его увеличивается, о чем можно судить по манометру: перепад уровней жидкости увеличивается.
При выравнивании температуры воздуха в баллоне и комнатной перемещение уровней жидкости прекратится, их разность станет постоянной и равной 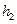 . В этом состоянии температура воздуха в баллоне равна
. В этом состоянии температура воздуха в баллоне равна 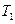 , его давление
, его давление 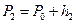 , масса и объем равны соответственно
, масса и объем равны соответственно 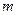 и
и 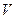 .
.
Можно выделить три различные состояния воздуха в баллоне с постоянным объемом 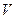 :
:
1) после установления равновесия при давлении 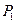 и температуре
и температуре 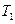 содержится масса воздуха
содержится масса воздуха 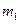 ;
;
2) после адиабатического расширения остается масса воздуха 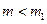 при атмосферном давлении
при атмосферном давлении 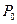 и температуре
и температуре 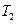 , ниже комнатной;
, ниже комнатной;
3) после установления температурного равновесия (масса 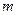 , температура
, температура 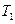 ) давление становится равным
) давление становится равным 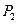 .
.
Переход из первого состояния во второе происходит адиабатически. Для него справедливо уравнение Пуассона:
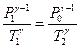 . .
| (11)
|
Поскольку переход из второго состояния в третье происходит без изменения объема (изохорический процесс), для него можно применить закон Гей-Люссака:
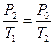 . .
| (12)
|
Исключив из (11) и (12) переменные 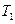 и
и 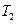 , получим:
, получим:
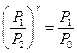 . .
| (13)
|
Логарифмируя уравнение (13), находим:
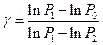 . .
| (14)
|
Разложим 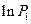 и
и  в ряд Тейлора:
в ряд Тейлора:
и
Ограничиваясь двумя первыми членами (это возможно, так как 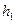 и
и 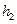 значительно меньше
значительно меньше 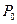 ), подставим их в (14) и получим окончательное выражение для вычисления отношения теплоемкостей:
), подставим их в (14) и получим окончательное выражение для вычисления отношения теплоемкостей:
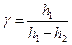 . .
| (15)
|
Порядок выполнения работы
1. Ознакомиться с установкой; разобраться с работой переключателя.
2. Для воздуха определить величину 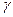 , измерив
, измерив 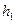 и
и 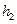 . Опыт повторить 9–11 раз, незначительно меняя первоначальную разность уровней в манометре.
. Опыт повторить 9–11 раз, незначительно меняя первоначальную разность уровней в манометре.
3. Вычислить: среднее значение 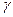 , абсолютную погрешность и ее среднее значение, ошибку опыта
, абсолютную погрешность и ее среднее значение, ошибку опыта 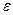 .
.
4. Сравнить полученное значение 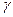 с табличными данными для воздуха.
с табличными данными для воздуха.
Контрольные вопросы
1. Дать описание всех изопроцессов, используя уравнение Менделеева–Клапейрона.
2. Что такое теплоемкость? Как связаны молярная и удельная теплоемкости? Почему теплоемкость газа зависит от условий нагревания?
3. Используя первое начало термодинамики, объяснить, почему 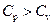 ? Вывести уравнение Майера.
? Вывести уравнение Майера.
4. Какой процесс называется адиабатическим? Вывести уравнение адиабаты для идеального газа.
5. Что происходит с внутренней энергией газа при адиабатическом расширении? Как при этом меняется температура газа?
6. На какой стадии опыта процесс является адиабатическим? Почему уровни жидкости в манометре устанавливаются не сразу, а лишь спустя некоторое время?
7. Описать ход эксперимента. Вывести рабочую формулу.
8. Получить теоретическое значение 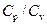 для двухатомного газа, используя принцип равномерного распределения энергии по степеням свободы.
для двухатомного газа, используя принцип равномерного распределения энергии по степеням свободы.
Список рекомендуемой литературы
13. Савельев И.В. Курс общей физики. М., 1977, 1982. т. 1. Гл. 10.
14. Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. Механика и молекулярная физика. М., 1965. Гл. 7, 8.
15. Рымкевич П.А. Курс физики. М., 1975. Гл. 5, 6.
Лабораторная работа № 7
Популярное:

