Скалярное произведение векторов
Термином (билинейные операции над векторами) иногда называют операции скалярного и векторного произведений двух векторов.
Определение. Скалярным произведением двух векторов  и
и  называют величину
называют величину 
 Cosф, где ф – угол между векторами. Обозначения
Cosф, где ф – угол между векторами. Обозначения 
 или (
или (  ,
,  ).
).
По этому определению двум векторам ставится в соответствие скаляр, который можно истолковать как работу постоянной по величине и направлению силы на прямолинейном участке пути.
Из определения вытекают простейшие свойства такого произведения.
1. 
 =
= 
 ; 2. С(
; 2. С( 
 )=(С
)=(С  )
)  . 3. (
. 3. (  +
+  )
) 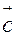 =
= 
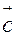 +
+ 
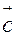 и 4.
и 4. 
 =0
=0
для ненулевых векторов, если векторы ортогональны (перпендикулярны).
Можно получить формулу для вычисления скалярного произведения,
если векторы заданы в координатной форме (своими координатами). Пусть  =ax
=ax  +ay
+ay 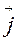 +az
+az  и
и  =bx
=bx  +by
+by 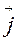 +bz
+bz  . Тогда
. Тогда 
 = ax bx +ay by +az bz. Т.к. при перемножении по свойству 3 с учетом определения остальные слагаемые будут равны нулю.
= ax bx +ay by +az bz. Т.к. при перемножении по свойству 3 с учетом определения остальные слагаемые будут равны нулю.
Из последнего соотношения следует, что 
 =
=  2.Читается – скалярный квадрат равен квадрату модуля.
2.Читается – скалярный квадрат равен квадрату модуля.
Из определения и полученных соотношений вытекают другие формулы. Например, для проекции одного вектора на другой получаем  =
=  . Условие перпендикулярности векторов axbx+ayby+azbz=0.
. Условие перпендикулярности векторов axbx+ayby+azbz=0.
2.3.Векторное произведение векторов
Определение. Векторным произведением двух векторов  и
и  называют вектор
называют вектор  , который:
, который:
-имеет модуль, равный произведению модулей перемножаемых векторов на синус угла меду ними - 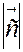 =
= 
 sinф;
sinф;
-ортогонален (перпендикулярен) каждому из векторов  и
и  (т.е. плоскости с векторами
(т.е. плоскости с векторами  и
и  );
);
-вместе с векторами  и
и  в порядке
в порядке  ,
,  ,
,  образует правую тройку векторов. Обозначают векторное произведение
образует правую тройку векторов. Обозначают векторное произведение 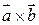 или [
или [  ,
,  ].
].
Комментарий. Классическое понятие правой тройки векторов  ,
,  ,
,  в указанном порядке: если наблюдать с конца любого вектора поворот от следующего за ним к предыдущему в направлении против часовой стрелки, то тройка векторов правая. В противном случае – левая.
в указанном порядке: если наблюдать с конца любого вектора поворот от следующего за ним к предыдущему в направлении против часовой стрелки, то тройка векторов правая. В противном случае – левая.
Примером правой тройки будет набор декартовых базисных векторов  ,
, 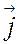 ,
,  . А в бытовом понятии правую тройку связывают с правым буравчиком (правой резьбой), когда при вращении по часовой стрелке буравчик (винт, гайка) продвигается вглубь от вращающего.
. А в бытовом понятии правую тройку связывают с правым буравчиком (правой резьбой), когда при вращении по часовой стрелке буравчик (винт, гайка) продвигается вглубь от вращающего.
Т.к. 
 sinф, то геометрически определение говорит о том, что площадь параллелограмма, построенного на множителях
sinф, то геометрически определение говорит о том, что площадь параллелограмма, построенного на множителях  и
и  равна модулю вектора
равна модулю вектора  .
.
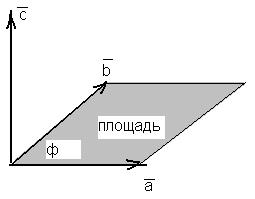
К определению 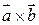
В качестве механической интерпретации векторного произведения может быть взят момент 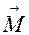 силы
силы 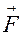 (постоянной по величине и направлению), приложенной к точке А относительно точки О. Вектор
(постоянной по величине и направлению), приложенной к точке А относительно точки О. Вектор 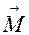 направлен так, что образует правую тройку с перемножаемыми векторами и численно равен величине
направлен так, что образует правую тройку с перемножаемыми векторами и численно равен величине 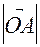
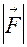 Sinф.
Sinф.

Механическая интерпретация 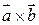 .
.
Справедливы следующие свойства векторного произведения.
С1.Для коллинеарных векторов  и
и  справедливо
справедливо 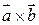 =0.
=0.
С2.  =
=  .
.
С3.  =l(
=l( 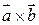 ).
).
Координатная форма вычисления 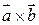 . Пусть
. Пусть  =ax
=ax  +ay
+ay 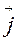 +az
+az  и
и  =bx
=bx  +by
+by 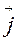 +bz
+bz  . Тогда
. Тогда 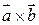 =(ax
=(ax  +ay
+ay 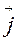 +az
+az  )х(bx
)х(bx  +by
+by 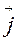 +bz
+bz  ). Далее используем взаимное расположение векторов
). Далее используем взаимное расположение векторов  ,
, 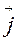 ,
,  и свойство 3 получим по определению
и свойство 3 получим по определению
axbx  х
х  +aybx
+aybx 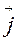 х
х  +azbx
+azbx  х
х  +aхbу
+aхbу  х
х 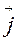 +aуby
+aуby 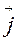 х
х 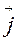 +azbу
+azbу  х
х 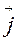 + +axbz
+ +axbz  х
х  +ay bz
+ay bz 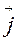 х
х  +az bz
+az bz  х
х  = (aхbу-aybx)
= (aхbу-aybx)  +( azbx- axbz)
+( azbx- axbz) 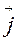 +
+
+( ay bz - azbу)  =
= 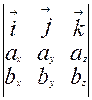 . Полученная символическая формула не противоречит ни свойствам определителя о смене знака при смене местами параллельных рядов, ни свойству векторного произведения о смене знака при смене порядка множителей. Из нее получается простое правило проверки коллинеарности векторов – равенство отношений
. Полученная символическая формула не противоречит ни свойствам определителя о смене знака при смене местами параллельных рядов, ни свойству векторного произведения о смене знака при смене порядка множителей. Из нее получается простое правило проверки коллинеарности векторов – равенство отношений 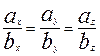 (или пропорциональность координат).
(или пропорциональность координат).
2.4.Смешанное произведение векторов
Рассмотрим произведения трех векторов:
((  ,
,  ),
), 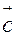 ) – уже известное нам произведение скаляра на вектор – и потому ничего нового;
) – уже известное нам произведение скаляра на вектор – и потому ничего нового;
[[  ,
,  ],
], 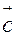 ] - двойное векторное произведение, которое имеет узкое приложение в механике;
] - двойное векторное произведение, которое имеет узкое приложение в механике;
([  ,
,  ],
], 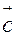 ) – векторно-скалярное (смешанное) произведение, которое имеет широкое применение в математике и приложениях.
) – векторно-скалярное (смешанное) произведение, которое имеет широкое применение в математике и приложениях.
Анализируя известное произведение [  ,
,  ] по Рис.2.2, можно получить геометрическую интерпретацию для смешанного произведения
] по Рис.2.2, можно получить геометрическую интерпретацию для смешанного произведения
([  ,
,  ],
], 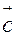 ). Модуль векторного произведения – площадь параллелограмма, построенного на векторах-множителях и равной
). Модуль векторного произведения – площадь параллелограмма, построенного на векторах-множителях и равной  =½
=½ 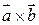 ½. Если теперь перемножить скалярно векторы
½. Если теперь перемножить скалярно векторы 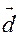 и
и 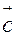 , то получим отрезок ОВ, равный высоте параллелепипеда, построенного на векторах-сомножителях
, то получим отрезок ОВ, равный высоте параллелепипеда, построенного на векторах-сомножителях  ,
,  ,
, 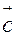 как на ребрах. Т.о., модуль ([
как на ребрах. Т.о., модуль ([  ,
,  ],
], 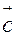 ) численно равен объему параллелепипеда, построенного на векторах множителях.
) численно равен объему параллелепипеда, построенного на векторах множителях.
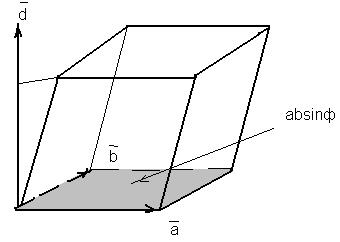
К определению ([  ,
,  ],
], 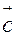 )
)
Используя координатную форму векторного произведения, получаем координатную форму смешанного произведения
([  ,
,  ],
], 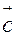 )=
)= 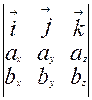 ( сx
( сx  +сy
+сy 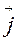 +сz
+сz  )=(( aхbу - aybx )
)=(( aхbу - aybx )  +( azbx- axbz)
+( azbx- axbz) 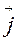 +( ay bz - azbу)
+( ay bz - azbу)  ) ) ( сx
) ) ( сx  +сy
+сy 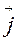 +сz
+сz  )=( aхbу - aybx ) сx +( azbx- axbz) сy +( ay bz - azbу) сz = =
)=( aхbу - aybx ) сx +( azbx- axbz) сy +( ay bz - azbу) сz = =  . Если в последнем определителе переставим местами 1-ю и 3-ю строки, то определитель не изменится и мы получим более удобную запись координат перемножаемых векторов в порядке их следования в произведении.
. Если в последнем определителе переставим местами 1-ю и 3-ю строки, то определитель не изменится и мы получим более удобную запись координат перемножаемых векторов в порядке их следования в произведении.
Из последней формулы для вычисления смешанного произведения следует возможность проверки компланарности (параллельности одной плоскости) трех векторов – если ([  ,
,  ],
], 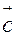 )=0, то векторы-множители компланарны. И следствием последнего равенства будет условие линейной зависимости трех векторов в пространстве.
)=0, то векторы-множители компланарны. И следствием последнего равенства будет условие линейной зависимости трех векторов в пространстве.
2.5.Типовые задачи, решаемые средствами векторной алгебры
Популярное:

