Неявные функции и их дифференцирование
Пусть  - дифференцируемая функция трех переменных
- дифференцируемая функция трех переменных 
 и
и 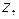 и пусть уравнение
и пусть уравнение 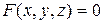 определяет
определяет  как функцию независимых переменных
как функцию независимых переменных  и
и  Частные производные этой неявной функции
Частные производные этой неявной функции  в точке
в точке 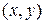 вычисляются по следующим формулам:
вычисляются по следующим формулам:
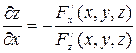 и
и 
при условии, что 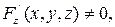 где
где  и
и 
Типовой пример
Найти частные производные 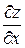 и
и  если
если  определяется, как функция от
определяется, как функция от  и
и  из уравнения
из уравнения
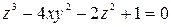 .
.
► Обозначим левую часть данного уравнения через 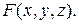 Тогда
Тогда
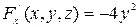 ,
,
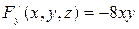 ,
,
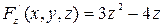 .
.
Отсюда получаем
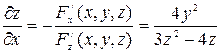 ;
; 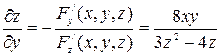 .◄
.◄
§6.Экстремум функции многих переменных
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Говорят, что точка
. Говорят, что точка  является точкой максимума (минимума) функции
является точкой максимума (минимума) функции  , если существует окрестность
, если существует окрестность 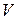 точки
точки  , такая что для любой точки
, такая что для любой точки 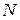 из этой окрестности
из этой окрестности 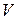 , отличной от точки
, отличной от точки  , справедливо неравенство
, справедливо неравенство 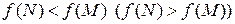 . Точки максимума и точки минимума функции называют точками экстремума функции, а значения функции в этих точках – экстремумами функции.
. Точки максимума и точки минимума функции называют точками экстремума функции, а значения функции в этих точках – экстремумами функции.
ТЕОРЕМА (необходимое условие экстремума). Если  – точка экстремума дифференцируемой функции
– точка экстремума дифференцируемой функции  , то
, то
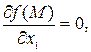
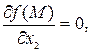 ...
...  . (1)
. (1)
Точка  , в которой выполнены условия (1), называется стационарной точкой. Не любая стационарная точка функции является точкой экстремума. Нижеследующая теорема достаточное условие для того, чтобы стационарная точка функции двух переменных была точкой экстремума.
, в которой выполнены условия (1), называется стационарной точкой. Не любая стационарная точка функции является точкой экстремума. Нижеследующая теорема достаточное условие для того, чтобы стационарная точка функции двух переменных была точкой экстремума.
ТЕОРЕМА (достаточное условие экстремума для функции двух переменных). Пусть  – стационарная точка функции двух переменных
– стационарная точка функции двух переменных 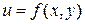 , дважды непрерывно дифференцируемой в некоторой окрестности точки М. Рассмотрим определитель
, дважды непрерывно дифференцируемой в некоторой окрестности точки М. Рассмотрим определитель
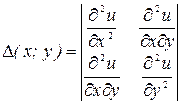 .
.
1. Если  , то
, то 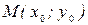 является точкой экстремума функции
является точкой экстремума функции 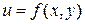 , а именно: а) если
, а именно: а) если 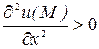 , то
, то  – точка минимума; б) если
– точка минимума; б) если  , то
, то  – точка максимума.
– точка максимума.
2. Если 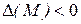 , то
, то  не является точкой экстремума.
не является точкой экстремума.
3. Если  , то нужны дополнительные исследования (экстремум может быть, а может отсутствовать)
, то нужны дополнительные исследования (экстремум может быть, а может отсутствовать)
Типовой пример
Найти точки экстремума функции
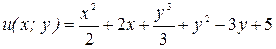 .
.
► Найдём стационарные точки функции  ,
, 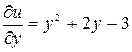 . Решим систему уравнений
. Решим систему уравнений


Решением системы являются точки 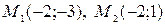 . Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:
. Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:
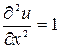 ,
, 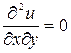 ,
,  .
.
Имеем
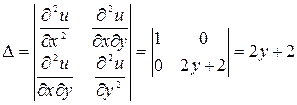 .
.
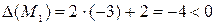 , следовательно,
, следовательно, 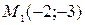 не является точкой экстремума.
не является точкой экстремума. 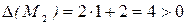 , что говорит о том, что
, что говорит о том, что  является точкой экстремума. А так как
является точкой экстремума. А так как 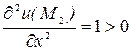 , то заключаем, что
, то заключаем, что 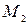 – точка минимума. ◄
– точка минимума. ◄
Приведём примеры, иллюстрирующие пункт 3.
1. 
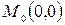 ─ точка возможного экстремума;
─ точка возможного экстремума; 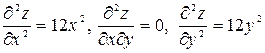 , следовательно, в точке
, следовательно, в точке  ,
,
однако в этой точке функция имеет минимум, т.к. 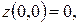 но
но 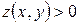 для всех точек из области определения.
для всех точек из области определения.
2. 
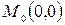 ─ точка возможного экстремума;
─ точка возможного экстремума; 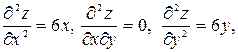 следовательно, в точке
следовательно, в точке  , однако в точке
, однако в точке 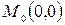 в этом случае экстремума нет. Так как
в этом случае экстремума нет. Так как 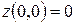 , а
, а 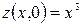 . Значит
. Значит 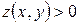 при
при 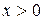 и
и 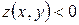 при
при  . Получили, что в любой окрестности точки
. Получили, что в любой окрестности точки 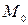 функция принимает значения разных знаков.
функция принимает значения разных знаков.
§7.Наибольшее и наименьшее значения функции многих переменных в замкнутой области
1. Точкой глобального максимума (минимума) функции 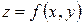 на множестве
на множестве 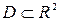 называется точка
называется точка 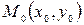 , в которой функция достигает своего наибольшего или наименьшего значения
, в которой функция достигает своего наибольшего или наименьшего значения
ТЕОРЕМА. Пусть в ограниченной и замкнутой области 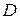 задана дифференцируемая функция
задана дифференцируемая функция 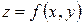 . Тогда эта функция достигает в области D своего наибольшего и наименьшего значения (так называемый глобальный экстремум).
. Тогда эта функция достигает в области D своего наибольшего и наименьшего значения (так называемый глобальный экстремум).
Эти значения могут достигаться либо в критических точках внутри области, либо на ее границе. Поэтому внутри области 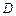 нужно найти все точки, в которых возможен экстремум. Затем, не выясняя, имеет ли функция
нужно найти все точки, в которых возможен экстремум. Затем, не выясняя, имеет ли функция 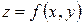 в этих точках экстремум, вычислить значения функции во всех найденных точках. Однако функция может принимать наибольшее и наименьшее значения и на границе области. Поэтому нужно отдельно найти наибольшее и наименьшее значения функции на границе области. При этом надо использовать уравнения границы, что позволяет уменьшить число независимых переменных у функции и свести задачу к исследованию функции одной переменной. Сравнивая все полученные таким образом значения функции, выбираем из них наибольшее и наименьшее.
в этих точках экстремум, вычислить значения функции во всех найденных точках. Однако функция может принимать наибольшее и наименьшее значения и на границе области. Поэтому нужно отдельно найти наибольшее и наименьшее значения функции на границе области. При этом надо использовать уравнения границы, что позволяет уменьшить число независимых переменных у функции и свести задачу к исследованию функции одной переменной. Сравнивая все полученные таким образом значения функции, выбираем из них наибольшее и наименьшее.
Типовой пример
Найти наибольшее и наименьшее значения функции 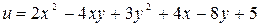 в замкнутой области (D), заданной неравенствами
в замкнутой области (D), заданной неравенствами 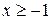 ,
, 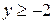 ,
, 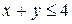 .
.
► 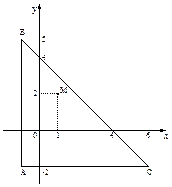 Изобразим область (D); она представляет собой треугольник с вершинами A|(-1; -2), B(-1; 5), C(6; -2). Найдём стационарные точки.
Изобразим область (D); она представляет собой треугольник с вершинами A|(-1; -2), B(-1; 5), C(6; -2). Найдём стационарные точки.  ,
, 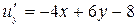 . Решим систему уравнений
. Решим систему уравнений


Решением этой системы является x=1, y=2. Стационарная точка M(1; 2) принадлежит области (D), так как её координаты удовлетворяют всем трём неравенствам, задающим треугольник (D). Найдём значение функции в этой точке: u(M) = 2 – 8 + 12 + 4 – 16 + 5 = –1.
Исследуем функцию на границе  области (D). Граница
области (D). Граница  представляет собой объединение трёх отрезков:
представляет собой объединение трёх отрезков: 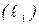 – отрезка BC,
– отрезка BC, 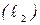 – отрезка AB,
– отрезка AB, 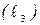 – отрезка AC.
– отрезка AC.
1)  .
. 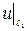 = 2x2 – 4x(4 – x) +
= 2x2 – 4x(4 – x) +
+ 3(4 – x)2 + 4x – 8(4–x) + 5 = 2x2 – 16x + 4x2 + 3(16 – 8x + x2) + 4x –
– 32 + 8x + 5 = 9x2 – 28x + 21. Найдём наибольшее и наименьшее значения функции 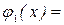 9x2 – 28x + 21 на отрезке [–1; 6]. Имеем
9x2 – 28x + 21 на отрезке [–1; 6]. Имеем 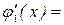 18x – 28; x = 14/9 – стационарная точка функции
18x – 28; x = 14/9 – стационарная точка функции 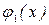 , 14/9 Î Î [–1; 6]. Обозначим N1(14/9; 4 –14/9 ) или N1(14/9; 22/9 ). u(N1) = =
, 14/9 Î Î [–1; 6]. Обозначим N1(14/9; 4 –14/9 ) или N1(14/9; 22/9 ). u(N1) = = 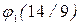 =196/9 – 392/9 + 21 = –34/9. Найдём значения
=196/9 – 392/9 + 21 = –34/9. Найдём значения 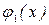 на концах отрезка [–1; 6]:
на концах отрезка [–1; 6]: 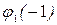 = u(B) = 58;
= u(B) = 58; 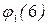 = u(C) = 177. Наибольшим из этих значений является u(C) = 177, наименьшим – u(N1) = – 34/9.
= u(C) = 177. Наибольшим из этих значений является u(C) = 177, наименьшим – u(N1) = – 34/9.
2) 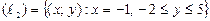 .
. 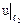 = 2 + 4y + 3y2 – 4 – 8y +
= 2 + 4y + 3y2 – 4 – 8y +
+5 = 3y2 – 4y + 3. Найдём наибольшее и наименьшее значения функции 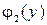 = 3y2 – 4y + 3 на отрезке [–2; 5];
= 3y2 – 4y + 3 на отрезке [–2; 5]; 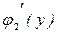 = 6y – 4; y = 2/3 – стационарная точка функции
= 6y – 4; y = 2/3 – стационарная точка функции 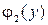 , принадлежащая отрезку [–2; 5]. Обозначим N2(–1; 2/3). U(N2) =
, принадлежащая отрезку [–2; 5]. Обозначим N2(–1; 2/3). U(N2) = 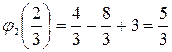 . Найдём значения функции
. Найдём значения функции 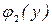 на концах отрезка [– 2; 5]:
на концах отрезка [– 2; 5]:  = u(A) = 23;
= u(A) = 23; 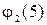 = u(B) = 58.
= u(B) = 58.
3) 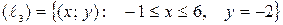 .
. 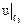 = 2x2 + 8x + 12 + 4x + + 16 + 5 = 2x2 + 12x + 33. Обозначим
= 2x2 + 8x + 12 + 4x + + 16 + 5 = 2x2 + 12x + 33. Обозначим  = 2x2 + 12x + 33.
= 2x2 + 12x + 33.
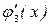 = 4x + 12. Стационарная точка x = – 3 не принадлежит отрезку
= 4x + 12. Стационарная точка x = – 3 не принадлежит отрезку
[–1; 6], поэтому она нас не интересует. Значения  на концах отрезка
на концах отрезка
[–1; 6] были найдены ранее: 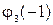 = u(A) = 23,
= u(A) = 23, 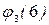 = u(C) = = 177.
= u(C) = = 177.
Сравнивая все полученные значения, находим  =u(C) =
=u(C) =
= u(6; –2) = 177, 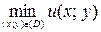 = u(M) = u(1; 2) = – 1. ◄
= u(M) = u(1; 2) = – 1. ◄
Типовой пример
Найти наибольшее и наименьшее значения функции 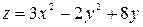 в области
в области 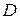 , заданной неравенствами:
, заданной неравенствами: 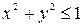 ,
,  .
.
► 
 1. Изобразим область:
1. Изобразим область:
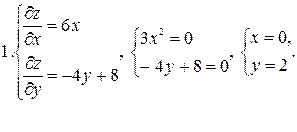
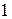

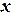
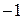
2. Точка  не принадлежит области
не принадлежит области 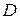 .
.
3. Граница  области
области 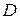 состоит из трех гладких частей
состоит из трех гладких частей 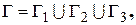 где
где 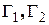 и
и 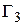 заданы уравнениями:
заданы уравнениями: 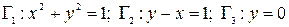 .
.
3.1. На части  границы
границы 
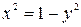 , следовательно на
, следовательно на 
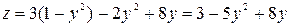 , где
, где 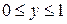 . Теперь встала задача нахождения наибольшего и наименьшего значения функции одной переменной
. Теперь встала задача нахождения наибольшего и наименьшего значения функции одной переменной 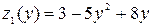 на промежутке
на промежутке 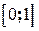 . Так как
. Так как 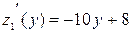 , то точка
, то точка  является стационарной точкой функции
является стационарной точкой функции  , и эта точка принадлежит промежутку
, и эта точка принадлежит промежутку 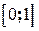 . Этому значению переменной
. Этому значению переменной  на
на  соответствует значение
соответствует значение 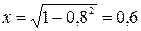 . Соответствующая точка -
. Соответствующая точка - 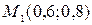 .
.
3.2. На части 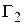 границы
границы 
 , следовательно, на
, следовательно, на 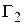
 , где
, где 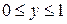 . Исследуем функцию
. Исследуем функцию 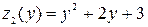 на промежутке
на промежутке 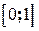 . Так как
. Так как  , то точка
, то точка 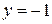 является стационарной точкой функции
является стационарной точкой функции 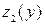 , но эта точка не принадлежит промежутку
, но эта точка не принадлежит промежутку 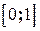 .
.
3.3. На части 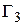 границы
границы 
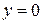 , следовательно на
, следовательно на 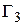
 , где
, где 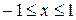 . Исследуем функцию
. Исследуем функцию 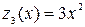 на промежутке
на промежутке 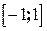 . Так как
. Так как 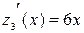 , то точка
, то точка 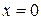 является стационарной точкой функции
является стационарной точкой функции  , и эта точка принадлежит промежутку
, и эта точка принадлежит промежутку 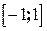 . Соответствующая точка
. Соответствующая точка 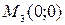 .
.
4. Таким образом, имеется всего пять точек, в которых нужно вычислить значения функции 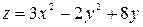 :
: 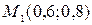 ;
; 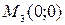 ;
; 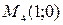 ;
; 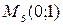 ;
; 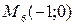 . В результате вычислений получаем:
. В результате вычислений получаем:  ;
;  ;
;  ;
; 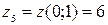 ;
; 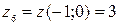 . Следовательно,
. Следовательно,  ,
, 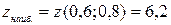
 . ◄
. ◄
Популярное:

