Условный экстремум функции двух переменных
Пример
Найти экстремум функции  при условии, что х и у связаны соотношением:
при условии, что х и у связаны соотношением: 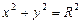 . Геометрически задача означает следующее: на эллипсе
. Геометрически задача означает следующее: на эллипсе 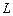 , полученном при пересечении цилиндра
, полученном при пересечении цилиндра  плоскостью
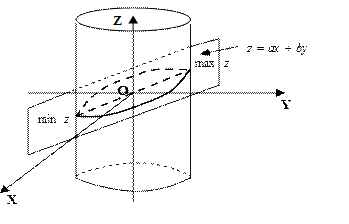
плоскостью  , требуется найти максимальное или минимальное значение аппликаты
, требуется найти максимальное или минимальное значение аппликаты  .
.
Эту задачу можно решать так: из уравнения  находим
находим  . Подставляя найденное значение у в уравнение плоскости, получаем функцию одной переменной х:
. Подставляя найденное значение у в уравнение плоскости, получаем функцию одной переменной х: 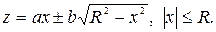
Тем самым задача о нахождении экстремума функции  при условии, что
при условии, что  , свелась к задаче нахождения экстремума функции одной переменной
, свелась к задаче нахождения экстремума функции одной переменной  , на отрезке
, на отрезке  .
.
Геометрически задача означает следующее: на эллипсе 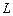 , полученном при пересечении цилиндра
, полученном при пересечении цилиндра  плоскостью
плоскостью  , требуется найти максимальное или минимальное значение аппликаты
, требуется найти максимальное или минимальное значение аппликаты  (рис.9). Эту задачу можно решать так: из уравнения
(рис.9). Эту задачу можно решать так: из уравнения  находим
находим  . Подставляя найденное значение у в уравнение плоскости, получаем функцию одной переменной х:
. Подставляя найденное значение у в уравнение плоскости, получаем функцию одной переменной х: 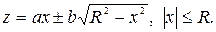
Тем самым задача о нахождении экстремума функции  при условии, что
при условии, что  , свелась к задаче нахождения экстремума функции одной переменной
, свелась к задаче нахождения экстремума функции одной переменной 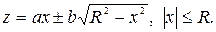 , на отрезке
, на отрезке  .
.
Итак, задача отыскания условного экстремума – это задача о нахождении экстремума целевой функции 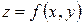 , при условии, что переменные х и у подчиняются ограничению
, при условии, что переменные х и у подчиняются ограничению  , называемому уравнением связи.
, называемому уравнением связи.
Будем говорить, что точка 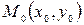 , удовлетворяющая уравнению связи, является точкой локального условного максимума (минимума), если существует окрестность
, удовлетворяющая уравнению связи, является точкой локального условного максимума (минимума), если существует окрестность 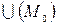 такая, что для любых точек
такая, что для любых точек  , координаты которых удовлетворяют уравнению связи, выполнено неравенство
, координаты которых удовлетворяют уравнению связи, выполнено неравенство  .
.
Если из уравнения связи можно найти выражение для у, то, подставляя это выражение в исходную функцию, превращаем последнюю в сложную функцию одной переменной х.
Общим методом решения задачи на условный экстремум является метод множителей Лагранжа. Составим вспомогательную функцию,  где
где  ─ некоторое число. Это функция называется функцией Лагранжа, а
─ некоторое число. Это функция называется функцией Лагранжа, а  ─ множителем Лагранжа. Таким образом, задача нахождения условного экстремума свелась к нахождению точек локального экстремума для функции Лагранжа. Для нахождения точек возможного экстремума надо решить систему из 3-х уравнений с тремя неизвестными х, у и.
─ множителем Лагранжа. Таким образом, задача нахождения условного экстремума свелась к нахождению точек локального экстремума для функции Лагранжа. Для нахождения точек возможного экстремума надо решить систему из 3-х уравнений с тремя неизвестными х, у и.
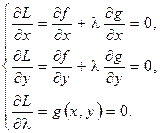
Затем следует воспользоваться следующим достаточным условием экстремума.
ТЕОРЕМА. Пусть точка  является точкой возможного экстремума для функции Лагранжа. Предположим, что в окрестности точки
является точкой возможного экстремума для функции Лагранжа. Предположим, что в окрестности точки  существуют непрерывные частные производные второго порядка функций
существуют непрерывные частные производные второго порядка функций  и
и 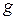 . Обозначим
. Обозначим
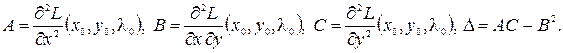 Тогда, если
Тогда, если  , то
, то  ─ точка условного экстремума функции
─ точка условного экстремума функции 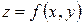 при уравнении связи
при уравнении связи  при этом, если
при этом, если  , то
, то  ─ точка условного минимума, если
─ точка условного минимума, если  , то
, то  ─ точка условного максимума.
─ точка условного максимума.
Градиент и производная по направлению
Пусть функция 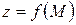 определена в некоторой (открытой) области. Рассмотрим любую точку
определена в некоторой (открытой) области. Рассмотрим любую точку  этой области и любую направленную прямую (ось)
этой области и любую направленную прямую (ось) 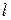 , проходящую через эту точку (рис. 1). Пусть
, проходящую через эту точку (рис. 1). Пусть  – какая-нибудь другая точка этой оси,
– какая-нибудь другая точка этой оси,  – длина отрезка между
– длина отрезка между 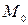 и
и  , взятая со знаком «плюс», если направление
, взятая со знаком «плюс», если направление  совпадает с направлением оси
совпадает с направлением оси 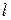 , и со знаком «минус», если их направления противоположны.
, и со знаком «минус», если их направления противоположны.
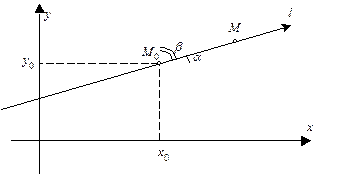
Рис. 1
Пусть  неограниченно приближается к
неограниченно приближается к 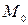 . Предел
. Предел
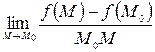
называется производной от функции  по направлению
по направлению 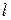 (или вдоль оси
(или вдоль оси 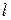 ) и обозначается следующим образом:
) и обозначается следующим образом:
 .
.
Эта производная характеризует «скорость изменения» функции в точке 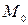 по направлению
по направлению 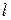 . В частности, и обычные частные производные
. В частности, и обычные частные производные  ,
,  также можно рассматривать как производные «по направлению».
также можно рассматривать как производные «по направлению».
Предположим теперь, что функция  имеет в рассматриваемой области непрерывные частные производные. Пусть ось
имеет в рассматриваемой области непрерывные частные производные. Пусть ось 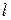 образует с осями координат углы
образует с осями координат углы 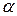 и
и 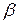 . При сделанных предположениях производная по направлению
. При сделанных предположениях производная по направлению  существует и выражается формулой
существует и выражается формулой
 .
.
Если вектор  задан своими координатами
задан своими координатами 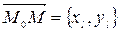 , то производную функции
, то производную функции  по направлению вектора
по направлению вектора  можно вычислить по формуле:
можно вычислить по формуле:
 .
.
Вектор с координатами 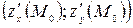 называется вектором-градиентомфункции
называется вектором-градиентомфункции  в точке
в точке 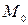 . Вектор-градиент указывает направление наиболее быстрого возрастания функции в данной точке.
. Вектор-градиент указывает направление наиболее быстрого возрастания функции в данной точке.
Пример
Дана функция 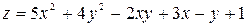 , точка A(1, 1) и вектор
, точка A(1, 1) и вектор  . Найти: 1) grad z в точке A; 2) производную в точке A по направлению вектора
. Найти: 1) grad z в точке A; 2) производную в точке A по направлению вектора  .
.
► Частные производные данной функции в точке  :
:
 ;
;  .
.
Тогда вектор-градиент функции в этой точке:  . Вектор-градиент еще можно записать с помощью разложения по векторам
. Вектор-градиент еще можно записать с помощью разложения по векторам  и
и  :
:
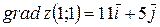 . Производная функции
. Производная функции 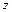 по направлению вектора
по направлению вектора  :
:
 . Итак,
. Итак,  ,
, 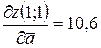 .◄
.◄
Метод наименьших квадратов.
В различных практических исследованиях приходится использовать формулы, полученные на основании опыта, наблюдения. Один из лучших способов получения таких формул – метод наименьших квадратов.
Пусть между переменными величинами  и
и  имеется или предполагается некоторая функциональная зависимость
имеется или предполагается некоторая функциональная зависимость  , подлежащая определению. С этой целью выполнены наблюдения, а результаты их представлены в таблице в виде n пар соответствующих значений переменных
, подлежащая определению. С этой целью выполнены наблюдения, а результаты их представлены в таблице в виде n пар соответствующих значений переменных  и
и  :
:
Эти данные можно представить графически, если в прямоугольной системе координат построить точки, координаты которых – пары соответствующих значений переменных  и
и  , т.е. точки
, т.е. точки 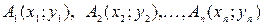 .
.
Графически это может выглядеть так:
 ,
,
или так:
 ,
,
а может быть и как-то иначе.
1. Предположим что анализ опытных данных (в том числе и расположение точек 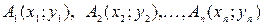 на плоскости) привел к выводу, что между переменными
на плоскости) привел к выводу, что между переменными  и
и  существует линейная зависимость
существует линейная зависимость
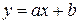 , (1)
, (1)
которая графически изображается прямой на плоскости.
Задача сводится к отысканию значений параметров a, b.
Для этого составим функцию  - сумма квадратов*) отклонений предполагаемых значений (аналитических) от фактических.
- сумма квадратов*) отклонений предполагаемых значений (аналитических) от фактических.
Исследуем эту функцию на экстремум. А точнее, по понятным причинам, нужно найти точки минимума.
Необходимое условие существования экстремума
 ,
,
т.е.
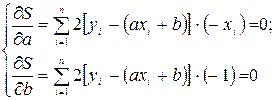 или
или  . (2)
. (2)
Решая эту систему линейных алгебраических уравнений относительно 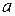 и
и  получаем их значения, а, следовательно, получаем аналитический вид линейной зависимости исследуемых величин.
получаем их значения, а, следовательно, получаем аналитический вид линейной зависимости исследуемых величин.
Пример
Данные о стоимости основных производственных фондов 5 предприятий  (млн. руб.) и среднесуточной переработки свеклы
(млн. руб.) и среднесуточной переработки свеклы  (тыс. ц.) приведены в таблице:
(тыс. ц.) приведены в таблице:
Предполагая, что между переменными  и
и  существует линейная зависимость, необходимо: а) найти, пользуясь способом наименьших квадратов, параметры этой зависимости; б) определить среднесуточную переработку свеклы предприятием, имеющим стоимость основных фондов 9 млн руб.
существует линейная зависимость, необходимо: а) найти, пользуясь способом наименьших квадратов, параметры этой зависимости; б) определить среднесуточную переработку свеклы предприятием, имеющим стоимость основных фондов 9 млн руб.
► Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (2) поместим в следующей таблице:
Следовательно, система нормальных уравнений при  =5 ( число
=5 ( число
пар значений переменных) имеет вид:
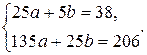
Решая ее, найдем: 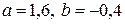 , а искомая функциональная зависимость такова:
, а искомая функциональная зависимость такова:  .
.
Среднесуточную переработку свеклы предприятием, имеющим стоимость основных фондов 9 млн. руб. найдем, подставив значение  в найденное уравнение зависимости между
в найденное уравнение зависимости между  и
и  :
:
 (тыс. ц. ) ◄
(тыс. ц. ) ◄
Типовой пример
Экспериментально получены пять значений искомой функции  при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию
при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию  в виде
в виде  .
.
 .
.
► Запишем нормальные уравнения для коэффициентов 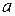 и
и  :
:
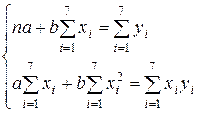
Составим вспомогательную таблицу:
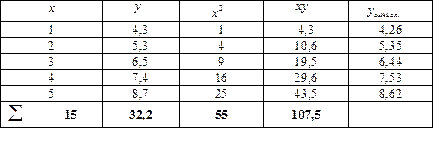
Подставим числовые значения в нормальные уравнения:
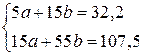 . Решив систему, получим
. Решив систему, получим  ;
;  . Искомая функция имеет вид:
. Искомая функция имеет вид: 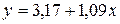 . В последнем столбце таблицы запишем значения
. В последнем столбце таблицы запишем значения  , вычисленные по полученной формуле
, вычисленные по полученной формуле 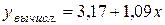 .◄
.◄
2.Если при нахождении  усматривается квадратичная зависимость, то ее следует искать в виде
усматривается квадратичная зависимость, то ее следует искать в виде  .
.
Тогда
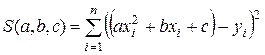 .
.
Необходимое условие существования экстремума
 т.е.
т.е. 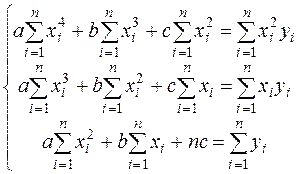 .
.
Решив эту систему уравнений, получаем значения  . А, следовательно, получаем аналитический вид квадратичной зависимости у от х.
. А, следовательно, получаем аналитический вид квадратичной зависимости у от х.
Типовой пример
Результаты наблюдений величины у от х:
| х
| -2
| -1, 5
| -1
| -0, 5
| 1, 5
| 2, 5
|
| 3, 5
|
| у
| 8, 8
| 8, 1
|
| 0, 5
| -4
| -7
| -8
| -9
|
Графически:

Определить: а) линейную зависимость у от х;
б) квадратичную зависимость у от х;
в) каково возможное значение у при х=6, 3.
а) Линейную зависимость ищем в виде  .
.
Для определения а, b следует составить и решить систему уравнений
 .
.
Система уравнений имеет вид:
 .
.
Решая ее любым известным способом, получаем a=-3, 2, b=0, 972.
Значит вид линейной зависимости  .
.
Графически:
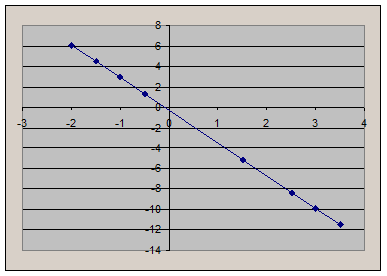
б) Для получения квадратичной зависимости поступаем аналогично. Вид квадратичной зависимости  .
.
Для нахождения коэффициентов a, b, c следует составить систему уравнений
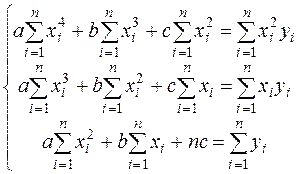
По данным наблюдений получаем систему уравнений:
 .
.
Решив эту систему, получаем аналитический вид квадратичной зависимости исследуемого процесса 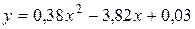 .
.
Графически:
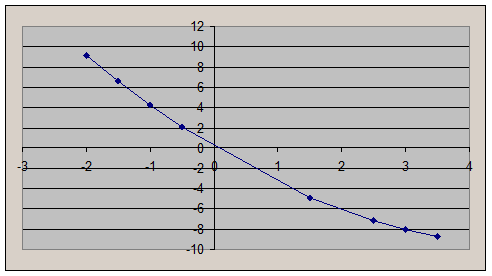
Судите сами, какая из полученных кривых точнее представляет изучаемый процесс.
в) При х=6, 3 при линейной зависимости значение у=-20, 466; при квадратичной зависимости у=-8, 95.
Распространяя действия полученных функций на всю область определения, можно интерполировать, экстраполировать исследуемый процесс.
Существенная разница результатов при экстраполировании в предыдущем примере означает лишь то, что нужны другие критерии (а не на первый взгляд из графика) для выяснения вида функции исследуемого процесса.
3. Пусть зависимость между переменными  и
и  выражается показательной функцией
выражается показательной функцией
 (3)
(3)
Логарифмируя обе части этого уравнения, получим
 .
.
Следовательно, между значениями переменной  и логарифмами
и логарифмами
значений переменной  существует линейная зависимость с параметрами
существует линейная зависимость с параметрами
 и
и  . Поэтому, если воспользоваться способом наименьших
. Поэтому, если воспользоваться способом наименьших
квадратов, то логарифмы 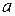 и
и  параметров функции (3) определяются из системы уравнений
параметров функции (3) определяются из системы уравнений
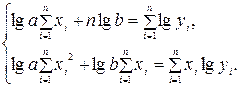 , (4)
, (4)
которая получена из системы (2) заменой в ней 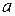 и
и  их логарифмами,
их логарифмами,
а  на
на  .
.
Типовой пример
Средняя годовая численность рабочих и служащих на некотором предприятии характеризуется следующими условными данными:
| Годы
|
|
|
|
|
|
|
|
| Числ - ть раб-х и служащих
| 12 168
| 13 531
| 18 990
| 22 249
| 22 325
| 23 581
| 24 770
|
Предполагая, что рост численности рабочих и служащих происходил по показательной кривой  , найти параметры
, найти параметры 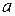 и
и  этой зависимости, пользуясь способом наименьших квадратов.
этой зависимости, пользуясь способом наименьших квадратов.
► Систему координат выберем так, чтобы 1995г. соответствовало ее начало - это упростит вычисления. Следовательно, при решении задачи исходим из следующих данных:
| Годы
| -3
| -2
| -1
|
|
|
|
|
| Численность рабочих и служащих
| 12 168
| 13 531
| 18 990
| 22 949
| 22 325
| 23 581
| 24 770
|
Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (4) располагаем в таблице:
| I
| 
| 
| 
| 
| 
|
|
| -3
-2
-1
|
| 4, 0852
4, 1313
4, 2785
4, 3608
4, 3488
4, 3726
4, 3939
|
| -12, 2556
-8, 2626 -24, 7967
-4, 2785
4, 3488
8, 7452 26, 2757
13, 1817
|
| Сумма
|
| -
| 29, 971
|
| -24, 7969+ 26, 2757=1, 4790
|
Подcтавим результаты вычислений в систему (4). Учитывая, что  = 7, а
= 7, а  , первое уравнение этой системы примет вид
, первое уравнение этой системы примет вид  , откуда
, откуда  , а тогда
, а тогда  .
.
Второе уравнение системы (4) принимает вид:
 , откуда
, откуда  , а тогда
, а тогда  .
.
Следовательно, искомая функциональная зависимость такова:
 .
.
Уравнение показывает, что численность рабочих и служащих в среднем росла ежегодно в 1, 129 раза или на 12, 9% ежегодно. ◄
4. В случаях, когда между переменными  и
и  существует гиперболическая зависимость
существует гиперболическая зависимость
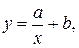 (5)
(5)
можно сказать, что между обратными значениями переменной  (т.е.
(т.е. 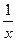 ) и значениями переменной
) и значениями переменной  существует линейная зависимость. Поэтому, если воспользоваться способом наименьших квадратов, то параметры
существует линейная зависимость. Поэтому, если воспользоваться способом наименьших квадратов, то параметры 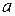 и
и  функции (5) определяются из следующей системы нормальных уравнений:
функции (5) определяются из следующей системы нормальных уравнений:
 , (6)
, (6)
которая получается из системы (2), если в ней  заменить на
заменить на 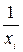 .
.
Типовой пример
В таблице приведены данные о стаже рабочего  (в годах) и затратах времени на обработку одной детали
(в годах) и затратах времени на обработку одной детали  (мин):
(мин):
Предполагая, что между переменными  и
и  существует гиперболическая зависимость
существует гиперболическая зависимость 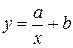 , найти параметры
, найти параметры 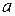 и
и  этой зависимости, пользуясь способом наименьших квадратов.
этой зависимости, пользуясь способом наименьших квадратов.
► Результаты вспомогательных вычислений поместим в таблице:

| 
| 
| 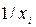
|  1/xi2 1/xi2
| 
|
|
|
|
|
|
|
|
|
|
|
| 1/3=0, 3333
| 1/9=0, 1111
| 9, 0000
|
|
|
|
| 1/5=0, 2
| 1/25=0, 04
| 4, 4
|
|
|
|
| 1/7=0, 1429
| 1/49»0, 0204
| 2, 5714
|
|
|
|
| 1/9»0, 1111
| 1/81»0, 0123
| 1, 8889
|
|
|
|
| 1/11»0, 0909
| 1/121»0, 0083
| 1, 4545
|
| å
| -
|
| 1, 8782
| 1, 1921
| 53, 3148
|
Подставляя полученные значения в систему (6) при  = 6 (число пар соответствующих значений переменных
= 6 (число пар соответствующих значений переменных  и
и  ), получим
), получим
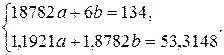 ,
,
Решая эту систему, найдем  ,
, 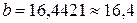 . Следовательно, искомая функциональная зависимость имеет вид:
. Следовательно, искомая функциональная зависимость имеет вид:
 ◄
◄
§10. Теория функций многих переменных и основные зависимости, используемые в экономике
1. Производственная функция
Функция, выражающая зависимость объёма производства от величины затраченных ресурсов, называется производственной функцией (ПФ).
Если  , то ПФ называется одноресурсной. В ряде случаев ПФ может быть сведена к зависимости производительности труда у (то есть выпуска продукта в расчёте на одного работника) от капиталовооруженности труда х (то есть величины капитала в расчёте на одного работника), где капиталовооруженность –
, то ПФ называется одноресурсной. В ряде случаев ПФ может быть сведена к зависимости производительности труда у (то есть выпуска продукта в расчёте на одного работника) от капиталовооруженности труда х (то есть величины капитала в расчёте на одного работника), где капиталовооруженность –  (здесь К – величина капитала,
(здесь К – величина капитала, 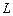 ─ численность занятых).
─ численность занятых).
Возникновение теории производственных функций относится к 1928 году. Тогда появилась статья американских учёных Д. Кобба и П. Дугласа, в которой впервые была введена функция, выражающая зависимость между объёмом основных фондов К, затратами труда 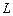 и объёмом выпускаемой продукции
и объёмом выпускаемой продукции 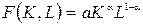 , где
, где  . График ПФКД в трёхмерном пространстве есть коническая поверхность (рис.1).
. График ПФКД в трёхмерном пространстве есть коническая поверхность (рис.1).
 Рис.1
Рис.1 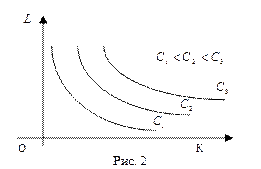
Для производственной функции двух переменных  линией уровня, соответствующей
линией уровня, соответствующей 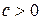 , является множество точек плоскости с неотрицательными координатами, удовлетворяющих условию
, является множество точек плоскости с неотрицательными координатами, удовлетворяющих условию  . Для функции Кобба-Дугласа
. Для функции Кобба-Дугласа  линии уровня, соответствующие
линии уровня, соответствующие 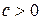 , задаются уравнением
, задаются уравнением  или
или  . Линии уровня функции
. Линии уровня функции  для различных значений
для различных значений 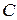 изображены на рис. 2.
изображены на рис. 2.
Точки  , лежащие на одной линии уровня, соответствуют различным наборам затрат, обеспечивающим один и тот же выпуск продукции.
, лежащие на одной линии уровня, соответствуют различным наборам затрат, обеспечивающим один и тот же выпуск продукции.
Линии уровня ПФ называются изоквантами. Отметим, что изокванта, соответствующая  , расположена «северо-восточнее» изокванты, соответствующей
, расположена «северо-восточнее» изокванты, соответствующей  .
.
Пример
Найдём изокванты производственной функции Кобба-Дугласа  . Изокванта этой функции, соответствующая значению
. Изокванта этой функции, соответствующая значению  , задана уравнением
, задана уравнением  или
или 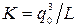 2.◄
2.◄
Далее выясним, какую экономическую интерпретацию можно дать частным производным ПФ. Отношение
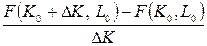
показывает, какой дополнительный выпуск приходится на 1 единицу изменения основных фондов 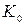 при постоянных затратах труда
при постоянных затратах труда  . Если существует конечный предел указанного выше отношения при
. Если существует конечный предел указанного выше отношения при 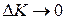 , то это есть частная производная функции
, то это есть частная производная функции 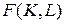 по переменной
по переменной 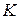
 .
.
Частная производная 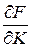 называется предельной фондоотдачей. Частная производная
называется предельной фондоотдачей. Частная производная  называется предельной производительностью труда и определяется аналогично
называется предельной производительностью труда и определяется аналогично
 .
.
Найдем в явном виде частные производные ПФ
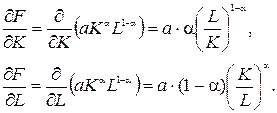
Эластичностью функции  в точке
в точке  по переменной
по переменной  называется предел
называется предел  , по переменной
, по переменной  – предел
– предел 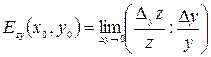 . Значит
. Значит  Эластичность приближённо показывает на сколько процентов изменится выпуск, если затраты какого-либо одного ресурса увеличатся на 1 % при неизменных объёмах другого ресурса.
Эластичность приближённо показывает на сколько процентов изменится выпуск, если затраты какого-либо одного ресурса увеличатся на 1 % при неизменных объёмах другого ресурса.
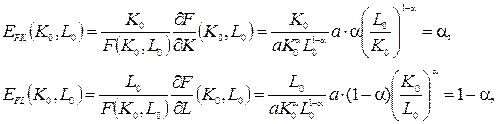
Экономический смысл параметра  . Эластичность выпуска по основным фондам равна
. Эластичность выпуска по основным фондам равна  . Значит, относительное изменение основных фондов
. Значит, относительное изменение основных фондов 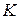 на 1 % вызывает относительное изменение выпуска на
на 1 % вызывает относительное изменение выпуска на  % (приблизительно), если считать изменение
% (приблизительно), если считать изменение 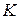 на 1% достаточно малым.
на 1% достаточно малым.
Пример
Функции спроса на товары  и
и 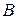 имеют вид:
имеют вид: 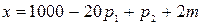 ;
; 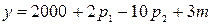
где  ,
, 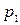 и
и  ,
, 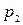 – спрос на товары
– спрос на товары  и
и 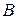 и их цены соответственно,
и их цены соответственно,  – часть дохода потребителя, которую он расходует на приобретение названных товаров. Определить коэффициенты эластичности функций при
– часть дохода потребителя, которую он расходует на приобретение названных товаров. Определить коэффициенты эластичности функций при 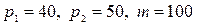 .
.
►
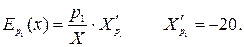
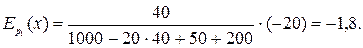
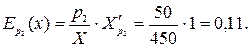
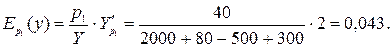
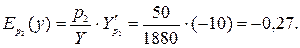
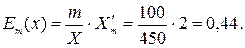
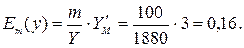
Величины  и
и  показывают, что с ростом цены товара
показывают, что с ростом цены товара  на 1%, спрос на товар
на 1%, спрос на товар  снижается на 1, 8%, а спрос на товар
снижается на 1, 8%, а спрос на товар 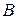 повышается на 0, 043%.
повышается на 0, 043%.
Аналогично величины  и
и  Ер2(у) показывают, что с увеличением цены товара
Ер2(у) показывают, что с увеличением цены товара 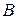 на 1%, спрос на товар
на 1%, спрос на товар  повышается на 0, 11%, а спрос на товар
повышается на 0, 11%, а спрос на товар 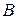 снижается 0, 27%.◄
снижается 0, 27%.◄
Пусть выпуск  является постоянным, (то есть все наборы затрачиваемых ресурсов расположены на одной изокванте), тогда полный дифференциал ПФ
является постоянным, (то есть все наборы затрачиваемых ресурсов расположены на одной изокванте), тогда полный дифференциал ПФ  тождественно равен нулю
тождественно равен нулю
 , здесь
, здесь  и
и 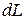 ─ дифференциалы переменных
─ дифференциалы переменных 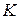 и
и 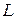 .
. 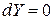 , значит,
, значит,  .
.
Отношение  является предельной нормой замены основного капитала трудом.
является предельной нормой замены основного капитала трудом.
2. Функция полезности. Задача потребительского выбора (ЗПР)
В основе модели поведения потребителей лежит гипотеза, что каждый из них, осуществляя выбор наборов благ при заданных ценах и имеющемся доходе, стремиться максимизировать уровень удовлетворения своих потребностей.
Пусть на рынке потребителю предлагается n различных наборов благ 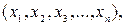 где
где  - количество i-го блага в натуральных единицах. Блага приобретаются по рыночным ценам
- количество i-го блага в натуральных единицах. Блага приобретаются по рыночным ценам  соответственно. Стоимость набора благ -
соответственно. Стоимость набора благ -  В распоряжении потребителя имеется ограниченное число денег R (доход). Ясно, что существует бюджетное ограничение
В распоряжении потребителя имеется ограниченное число денег R (доход). Ясно, что существует бюджетное ограничение 
Полезность блага – это способность удовлетворять ту или иную потребность. Потребитель выбирает наиболее предпочтительный набор среди всех доступных. В XIX веке была введена функция полезности для предпочтения одного набора другому. Основное ее свойство в том, что потребитель предпочитает набор X, а не Y, если u(X)> u(Y), то есть она упорядочивает наборы по предпочтению.
 Рис.3.
Рис.3.
Рассмотрим пространство двух благ (товаров). Функция полезности  – это субъективная числовая оценка полезности u набора товаров (x, y). Линии уровня функции полезности называют кривыми безразличия. Так как если
– это субъективная числовая оценка полезности u набора товаров (x, y). Линии уровня функции полезности называют кривыми безразличия. Так как если  то потребителю безразлично, каким набором обладать, так как они имеют одинаковую полезность.
то потребителю безразлично, каким набором обладать, так как они имеют одинаковую полезность.
Чем «северо-восточнее» расположена кривая безразличия, тем большему уровню она соответствует (рис.3). Кривые безразличия являются убывающими.
В теории потребительского выбора большую роль играют предельные по
Популярное:

