Частные производные функции двух переменных. Дифференцируемость функции двух переменных
Пусть в области D задана функция  . Если считать
. Если считать  постоянным, то функция
постоянным, то функция  будет функцией одной переменной x. Значит можно рассматривать её производную по
будет функцией одной переменной x. Значит можно рассматривать её производную по  . Если считать x постоянным, то
. Если считать x постоянным, то  будет функцией по переменной
будет функцией по переменной  , и можно рассматривать производную по
, и можно рассматривать производную по  .
.
Возьмем т.  , найдем
, найдем  . Дадим
. Дадим  приращение
приращение 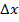 , а
, а  оставим неизменным. Получим т.
оставим неизменным. Получим т.  , найдем
, найдем 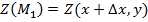 . Функция
. Функция  получит приращение
получит приращение  – частное приращение функции
– частное приращение функции 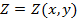 по переменнойx .
по переменнойx .
Аналогично, если  получит приращение
получит приращение  , а
, а  сохраняет постоянное значение, то функция
сохраняет постоянное значение, то функция  получит приращение
получит приращение  – частное приращение функции
– частное приращение функции 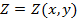 по переменной
по переменной 
Если  получит приращение
получит приращение 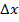 , а
, а  приращение
приращение  , то функция
, то функция  получит приращение
получит приращение 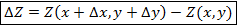 – полное приращение функции
– полное приращение функции 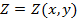

Определение: Частной производной функции 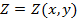 по
по  называется предел отношения частного приращения
называется предел отношения частного приращения  по
по  к приращению аргумента
к приращению аргумента 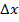 при
при 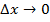
Обозначается:  ;
;  ;
; 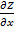

Определение: Частной производной функции 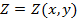 по
по  называется предел отношения частного приращения
называется предел отношения частного приращения 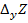 по
по  к приращению аргумента
к приращению аргумента  при
при 

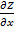 вычисляется в предположении, что
вычисляется в предположении, что 
 вычисляется в предположении, что
вычисляется в предположении, что 
Частные производные вычисляются по тем же правилам и формулам, что и производные функции одной переменной.
Примеры:
1) 
 ;
; 


2) 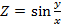
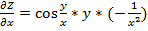 ;
; 
3) Доказать, что  удовлетворяет уравнению
удовлетворяет уравнению 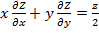
Решение:
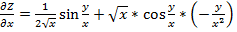 ;
; 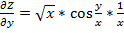
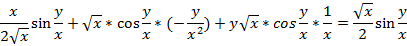

Определение: Функция 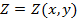 называется дифференцируемой в т.
называется дифференцируемой в т.  , если её полное приращение в этой точке можно представить в виде
, если её полное приращение в этой точке можно представить в виде
 (1)
(1)
где 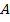 и
и  – постоянные (не зависят от
– постоянные (не зависят от  а зависят от координат т.
а зависят от координат т.  )
)
 при
при 
(1) можно записать в виде 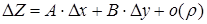 , где
, где  – расстояние от т.
– расстояние от т. 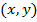 до т.
до т. 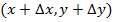 . Слагаемое
. Слагаемое  , линейное относительно
, линейное относительно 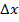 и
и  , называют главной частью приращения функции.
, называют главной частью приращения функции.
ТЕОРЕМА 1. Если функция 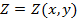 дифференцируема в т.
дифференцируема в т. 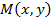 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
ТЕОРЕМА 2. ( необходимое условие дифференцируемости функции ) Если функция  дифференцируема в т.
дифференцируема в т.  , то она имеет в этой точке частные производные
, то она имеет в этой точке частные производные 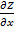 ,
,  , причем
, причем 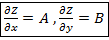 (2)
(2)
ТЕОРЕМА 3. ( достаточное условие дифференцируемости функции ) Если функция 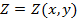 имеет частные производные в некоторой окрестности т.
имеет частные производные в некоторой окрестности т.  , непрерывные в самой этой точке, то она дифференцируема в этой точке.
, непрерывные в самой этой точке, то она дифференцируема в этой точке.
Замечание. Для функции одной переменной понятия «дифференцируемости» и «существования производной» равносильны. Для функции нескольких переменных (в частности двух) утверждения «функция дифференцируема в данной точке» не равнозначно утверждению «функция имеет частные производные по всем переменным в этой точке».
Полное приращение и полный дифференциал функции двух переменных
Из формул (1) и (2) предыдущего параграфа получим, что если 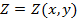 дифференцируема в т.
дифференцируема в т.  , то ее полное приращение в этой точке можно представить в виде
, то ее полное приращение в этой точке можно представить в виде 
Определение: Если функция 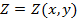 дифференцируема в т.
дифференцируема в т.  , то главная, линейная относительно
, то главная, линейная относительно 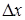 и
и  часть приращения функции, то есть выражение
часть приращения функции, то есть выражение  называется полным дифференциалом функции
называется полным дифференциалом функции 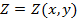 и обозначается
и обозначается  .
.
Приращения 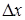 и
и  называются дифференциалами независимых переменных x и y.
называются дифференциалами независимых переменных x и y.
Итак,  – полный дифференциал функции
– полный дифференциал функции 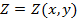
Пример: Найти полный дифференциал 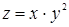 в произвольной точке
в произвольной точке
Решение. 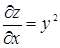 ,
,  ,
, 
 ,
,  – непрерывны на всей плоскости Oxy
– непрерывны на всей плоскости Oxy 
 существует в любой точке Oxy.
существует в любой точке Oxy.
Замечание.  ,
, 
Полный дифференциал применяется к приближенным вычислениям.



Дифференцирование сложной функции
Пусть дана функция  , где
, где  ,
,  – функции от t. Тогда
– функции от t. Тогда  – сложная функция от t, а переменные x и y – промежуточные аргументы.
– сложная функция от t, а переменные x и y – промежуточные аргументы.
Пусть  ,
,  имеют производные в точке t, а
имеют производные в точке t, а  в соответствующей точке
в соответствующей точке  дифференцируема.
дифференцируема.
Найдем  , зная
, зная  ,
,  и
и 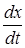 ,
, 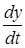 . Дадим t приращение
. Дадим t приращение 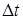 , тогда x и y получат приращения
, тогда x и y получат приращения 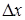 ,
,  , а z приращение
, а z приращение 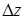 . Функция z дифференцируема, значит
. Функция z дифференцируема, значит
 , где
, где  при
при  .
.
Разделим на 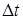 :
: 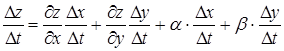
Устремим  :
: 
Если  , то
, то 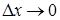 и
и  , так как
, так как  и
и  непрерывны
непрерывны
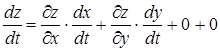
 (1) - производная сложной функции
(1) - производная сложной функции  , где
, где  ,
, 
Пример:  ,
,  ,
, 

 ,
,  ,
,

Замечание. Рассмотрим функцию  , где
, где  ,
, 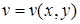 . Тогда
. Тогда  – сложная функция и ее частные производные вычисляются по формулам (при условии дифференцируемости соответствующих функцийее частные производные вычисляются по формулам ()):
– сложная функция и ее частные производные вычисляются по формулам (при условии дифференцируемости соответствующих функцийее частные производные вычисляются по формулам ()):



Полная производная
Рассмотрим функцию  , где
, где  . Переменная z есть функция одной переменной х:
. Переменная z есть функция одной переменной х:  . Тогда из
. Тогда из  , где вместо t рассматривать переменную х, получаем
, где вместо t рассматривать переменную х, получаем  (2) – формула полной производной
(2) – формула полной производной
Пример:  ,
,  ,
,  ,
, 
Решение. 

Производная неявной функции
Пусть функция y от х задана уравнением  , то есть задана неявно.
, то есть задана неявно.
Пусть  ,
,  ,
,  непрерывны в окрестности т.
непрерывны в окрестности т.  , координаты которой удовлетворяют уравнению
, координаты которой удовлетворяют уравнению  , причем
, причем  .
.


 По формуле (2) получим
По формуле (2) получим 

 – производная неявной функции
– производная неявной функции
Пример:  Найти
Найти  в точке
в точке 
Ответ:  ,
, 
Популярное:

