Если а – число элементов множества А и множество А разбито на b попарно непересекающихся подмножеств, то частным чисел а и b называется число элементов каждого подмножества разбиения.

⇐ ПредыдущаяСтр 17 из 20Следующая ⇒

Если а – число элементов множества А и множество А разбито на попарно непересекающиеся подмножества, в каждом из которых b элементов, то частным чисел а и b называется число подмножеств разбиения.

Действие, при помощи которого находят частное, называется делением, число а – делимым, число b – делителем.

Б) Сформулировать определение частного через произведение и доказать правила деления (по выбору).

Деление трехзначного числа на однозначное:

822: 6=

Представим 822 в виде суммы удобных слагаемых, чтобы каждое слагаемое делилось на 6, без остатка

822: 6=(600+180+42): 6=

Разделим каждое слагаемое в отдельности на 6

822: 6=(600+180+42): 6=(600: 6)+(180: 6)+(42: 6)=100+30+7=

Сложим полученные результаты

822: 6=(600+180+42): 6=(600: 6)+(180: 6)+(42: 6)=100+30+7=137

2. Подберите задания из учебника «Математика», в которых прослеживается последовательность приведенных ниже случаев деления:

Деление трехзначного числа на однозначное при трехзначном и двузначном частном.
Деление четырехзначного числа на однозначное при четырехзначном и трехзначном частном.
Деление пяти- шестизначных чисел.
Частные случаи деления (нули на конце или в середине частного).
Письменное деление с остатком.
Деление с остатком, когда на конце частного нуль.

(УЧЕБНИКА НЕТ, ПОТОМ ДОБАВЛЮ)

МДК 01.06 Методика обучения продуктивным видам деятельности с практикумом:

Технологическая карта урока.

Ф.И.О.

Класс: 2

3.Дата:

4.Предмет: Изобразительное искусство.

5. Тема урока: Каждый художник урожай своей земли хвалит.

5.Место и роль урока в изучаемой теме: урок изучение нового материала

6. Цель урока: способствовать усвоению традиций народных промыслов России, с изображением натюрморта.

Задачи

o образовательные: - научить технике рисования с натуры, подбору красок, цветовой гаммы, тени, расположению на листе;

o Развивающие: развивать умение переносить увиденное на лист с учетом формы и цвета; развивать наблюдательность и внимательность, познавательные интересы учеников через исследовательскую работу;

o Воспитательные: воспитывать любовь к окружающей природе, способность чувствовать красоту окружающего мира, экологическую культуру, усилить эмоциональное восприятие природы при шедевров живописи; воспитывать уважительное отношение к труду земледельца;

8. Оборудование: иллюстарции репродукций: натюрморты с овощами, простые карандаши, альбомы, резинки, акварельные краски, кисти; образец педагогического рисунка «Натюрморт с овощами».

Характеристика этапов урока

Название этапа	Содержание этапа	Деятельность учителя	Деятельность учащихся	Результат
1. Мотивация (самоопределение) к учебной деятельности.	Организационный момент Водная бесседа	Приветствие. Здравствуйте, ребята! сегодня я проведу у вас урок изобразительного искусства. - Ребята, давайте вспомним, что такое «живопись»? - Какие жанры живописи вы знаете?	Приветствие учителя. -Живопись – это такой вид изобразительного искусства, в котором цвет играет главную роль»; «Живопись означает писать жизнь, писать живо, т.е. полно и убедительно передавать действительность» - портрет, натюрморт, пейзаж, анималистический жанр, мифологический жанр.	Формирование УУД: (Р) волевая саморегуляция –самоопределение (Л); –смыслообразова ние (Л); – целеполагание (П);
2.Учебно-познавательная деятельность. Актуализация и фиксирование индивидуального затруднения в пробном действии.	Сообщение темы	-Сегодня на уроке мы будем выполнять натюрморт в цвете акварельными красками. Кто скажет, что такое натюрморт? -«Натюрморт» в переводе с французского означает «мертвая натура», т.е. «натюрморт» – это постановка из неживых предметов, предметов быта, домашнего обихода. В переводе с немецкого «натюрморт» – означает «тихая жизнь» - Натюрморты каких художников вы знаете? - На прошлом уроке мы с вами писали цветы, а сегодня научимся писать овощи (фрукты) -Как думаете, зачем люди тратят время и силы на выращивание овощей и фруктов? -Верно. - Это основа основ нашей жизни – пища. Нет пищи – нет жизни. Теме урожая посвящено много стихов, историй, картин, музыкальных произведений, где чествуют труд и прославляют земледельцев. И, конечно, выражают эстетическое восхищение формой, цветом, ароматом. - Сегодня наш урок посвящен урожаю. Но так как все объекты урожая людей мы не сможем объять, то остановимся на некоторых. Угадайте, о чем идет речь? Зоркий глаз – Богатырь Тарас В подземелье ушел, Десять братье нашел. Посмотри- ка, посмотри, Каковы богатыри! Вывешивается картинка - иллюстрация с картофелем. -Любопытный красный нос По макушку в землю врос, Лишь торчат на грядке Зеленые прядки Вывешивается картинка - иллюстрация с морковью… -На троне в зеленой короне Царь сидит на припеке, И лоснятся от важности красные щеки. Ветер поднялся, трон зашатался, Царь удивился, с трона свалился.	-это какая либо постановка. -перечисляют -чтобы потом ими питаться -Картофель - Морковка -Помидор	Р) самоконтроль: учатся отличать верно выполненное задание от неверного; осознание того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения. (К) умение выражать свои мысли с достаточной полнотой и точностью; умение слушать и понимать речь других. (П) формирование мыслительных операций: анализ, сравнение, обобщение.
3.Постановка проблемы. Выявление места и причины затруднения.	Исследование композиции, цветового решения Исследование композиции, цветового решения	- Ребята, обратите внимание на композицию натюрморта. - Как расположены овощи? - Какой овощ позади, а который впереди, слева и справа? - Какие овощи крупным планом, а какие «спрятались»? -Какой формы эти овощи, на какие геометрические фигуры похожи? -Какого цвета овощи, какие оттенки? -Где и как расположена тень? -Во-первых, сделаем набросок будущей картины. Берем простой карандаш и легкими движениями, чуть прикасаясь к листу, оформляем композицию. -Не забываете о расположении и величине композиции на листе. -Сначала рисуем овощ, который находится в центре, его отчетливо видно целиком. Передаем форму овощей: картофель продолговатый, морковь похожа на очень вытянутый треугольник, помидор как приплюснутый шар. Самая большая - это картофелина. Помидор поменьше, но покруглее. Морковь самая тонкая, но самая длинна. Не забудьте нарисовать у помидора и у моркови хвостики. -Во-вторых, начнем окрашивать самые светлые места Для этого на тонкую кисточку набираем краску и сначала рисуем округлые линии. Потом берем более темную краску и продолжаем наносить. -Стараемся сделать так, чтобы у всех овощей появился объем. Окрашиваем, делая тонкой кисточкой мазки так, чтобы все линии передавали форму овощей. -Не забывайте, что для достижения нужного цвета краски можно смешивать. Используйте таблицу смешивания красок, и ваши палитры. -В-третьих, когда овощи немного подсохнут, доработайте более тонкие места: веточки, хвостики, др. -В-четвертых, обратите внимание на фон: он тоже с одной стороны светлее, с дугой – темнее. Выполните сначала фон, а после того, как он подсохнет – нанесите тени. -Не забудьте подписать свою работу и поставить дату.	-они расположенные рядом друг с другом Позади тыква, впереди перец а справа гранат Овощи крупным планом изображены те которые сзади, а спрятались те которые ближе. -круглые, прямоугольные, похожи на круг и прямоугольник	Формирование УУД: (Р) проговаривание последовательность действий на уроке; формирование познавательной инициативы. (К) умение выражать свои мысли с достаточной полнотой и точностью; умение слушать и понимать речь других; учитывать разные мнения.

Задание № 22

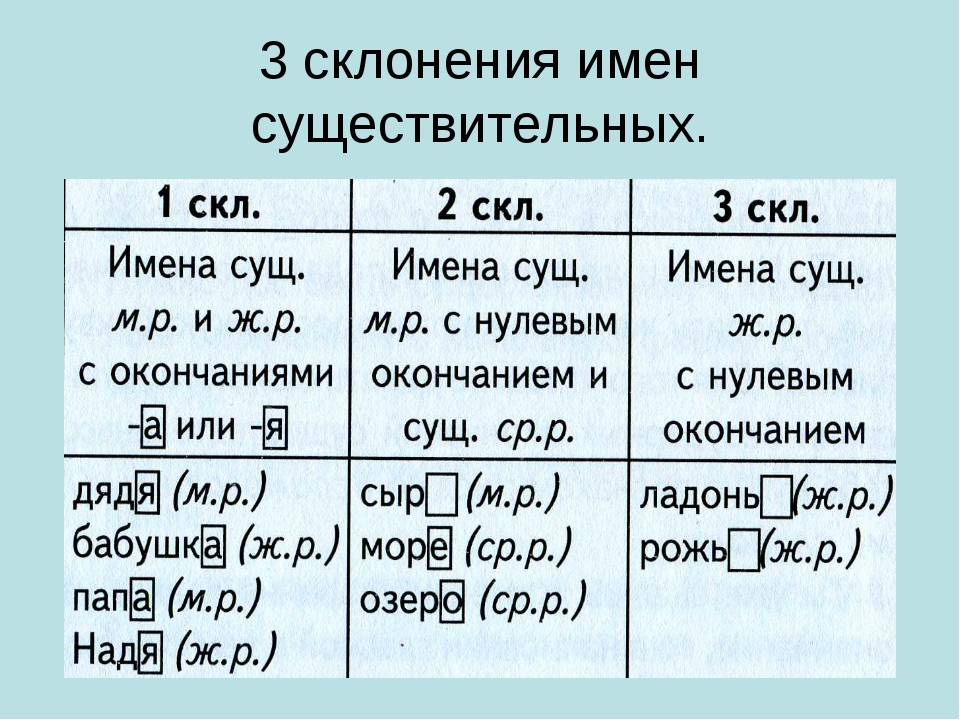Русский язык

Склонение слова СТЕНА и примеры к заданию.

Шампунь - одно из самых распространенных средств по уходу за волосами.

Слово ШАМПУНЬ - существительное, единственное число, мужское род, 2 склонение

И. п. (вопрос что) - шампунь

Р. п. (вопрос чего) - шампуня (в данном случае можно воспользоваться вопросом: нет чего)

Д. п. - (вопрос чему) - шампуню (подсказка: рад чему? )

В. п. (вопрос что) - шампунь

Т. п. (вопрос чем) - шампунем (подсказка: горжусь чем? )

П. п. (вопрос о чем) - о шампуне (думаю о чем? )

Во множественном числе это слово будет выглядеть так:

И. п. - шампуни

Р. п.- шампуней

Д. п. - шампуням

В. п. - шампуни

Т. п. - шампунями

П. п. - о шампунях

Слова «Речь», являются существительными неодушевлёнными женского рода третьего склонения.

И. (что? ) речь

Р. (чего? ) речи

Д. (чему? ) речи

В. (что? ) речь

Т. (чем? ) речью

П. (о чём? ) речи

Математика

1. Пусть f(x) и g(x) – два выражения с переменной х и областью определения Х. Тогда высказывательная форма вида f(x) = g(x)называется уравнением с одной переменной.

Значение переменной х из множества Х, при котором уравнение обращается в истинное числовое равенство, называется корнем уравнения (или его решением). Решить уравнение – это значит найти множество его корней.

Множество значений переменной, при которых выражения f(x) и g(x) имеют смысл, называется областью определения уравнения
f(x) = g(x). Множество решений уравнения является подмножеством области его определения.

Чтобы решить какое-либо уравнение, его сначала преобразовывают, заменяя другим, более простым; полученное уравнение опять преобразовывают, заменяя более простым, и т.д. Этот процесс продолжают до тех пор, пока не получают уравнение, корни которого можно найти известным способом. Но чтобы эти корни были корнями заданного уравнения, необходимо, чтобы в процессе преобразований получились уравнения, множества корней которых совпадают. Такие уравнения называются равносильными.

Равносильность уравнений

Определение. Два уравнения с одной переменой

f(x)=g(x) и h(x)=q(x)

называются равносильными, если множества решений этих уравнений совпадают.
Два уравнения равносильны, если у них одинаковые корни или если у них нет решений.

Давайте приведем пример равносильных уравнений.
Уравнения x2− 9=0 и (x+3)(3x− 27)=0 равносильны, т.к. имеют одинаковые корни х=±3. Уравнения x2+9=0 и 3x+27=0, также равносильны, поскольку не имеют вещественных корней.

Определение. Если каждый корень уравнения 1: f(x)=g(x) является в тоже время корнем уравнения 2: h(x)=q(x), то уравнение 2 является следствием уравнения 1.

Например, уравнение х− 3=3 имеет корень х=6, а уравнение (x− 3)2=9 имеет два корня х=6 и х=0. Один из корней совпадает, тогда уравнение (x− 3)2=9является следствием уравнения х− 3=3.
Два уравнения являются равносильными, тогда и только тогда, когда каждое из уравнений является следствием другого уравнения.

⇐ Предыдущая 11 12 13 14 15 161718 19 20 Следующая ⇒