
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Методы решения игр в смешанных стратегиях
Рассчитаем стратегию Пусть Пусть игрок 1 применит свою смешанную стратегию
Средний выигрыш игрока 1 должен удовлетворять условию
Введем обозначение С помощью введенных обозначений получаем:
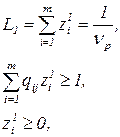  , (11) , (11)
Так как игрок 1 стремится максимизировать свой выигрыш, то частоты
Таким образом, задача определения оптимальной стратегии игрока 1 свелась к задаче линейного программирования. Аналогичным образом можно найти оптимальную стратегию игрока 2. При этом задача сводится к отысканию максимума величины
при следующих ограничениях:
где Эти задачи образуют пару двойственных задач линейного программирования. Первоначальная при этом называется исходной, или прямой. Связь исходной и двойственной задач заключается главным образом в том, что решение одной из них может быть получено непосредственно из решения другой. При этом в двойственной задаче линейного программирования коэффициентами целевой функции являются правые части ограничений исходной задачи и наоборот. В нашем примере ограничения для первого игрока выглядят следующим образом:
Найдя методами линейного программирования L1=L2; zi1,
3. Содержание домашней подготовки 3.1. Ознакомиться с целью выполнения работы, теоретическими сведениями. 3.2. Подготовить ответы на контрольные вопросы.
Порядок выполнения работы
4.1. Рассчитать сумму контрактов, заключенных первым игроком, для всех сочетаний выбранных типов продукции первой и второй фирмами по формулам (1), (2), (3) и составить платежную матрицу. 4.2. Упростить матрицу, проверить на наличие седловой точки, найти minmax и maxmin. 4.3. Рассчитать на основе платежной матрицы игрока 1, используя программу «doub2» и формулы (15), (16), (17), оптимальную стратегию игрока 2, цену игры и оптимальную стратегию игрока 1 на основе двойственных оценок, выдаваемых программой.
Отчет о работе
5.1. Цель работы. 5.2. Платежная матрица (в зависимости от варианта задания). 5.3. Оптимальные стратегии фирм и цена игры. 6. Контрольные вопросы
6.1. Основные этапы нахождения оптимальной стратегии. 6.2. Порядок упрощения платежной матрицы. 6.3. Решение игр в смешанных стратегиях. 6.4. Решение игры с седловой точкой.
Варианты заданий Пусть время подготовки производства одинаково для 1-й и 2-й фирм и всех вариантов.
Время подготовки производства
Дневная потребность заказчика (d) - 1 шт., продолжительность проекта (Т) - 60 дней. Время начала осуществленияпроекта (t0) для нечетных вариантов - 30 дней, для четных - 40 дней. Продолжительность первого контракта - 10 дней, последующих - 25 дней.
Доля первой фирмы fij, %, в сумме контрактов при готовности обеих фирм к производству
Приложение
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 672; Нарушение авторского права страницы