Тема: первообразная или неопределенный интеграл
Определение. Функция  называется первообразной функции
называется первообразной функции  на отрезке
на отрезке 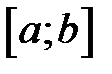 , если для всех точек этого интервала выполняется равенство
, если для всех точек этого интервала выполняется равенство  .
.
Теорема 1: Если  и
и  две первообразные функции
две первообразные функции 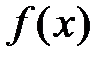 , то разность между ними равна постоянному числу.
, то разность между ними равна постоянному числу.
Доказательство: Рассмотрим разность 
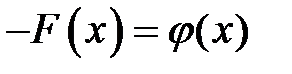 . Тогда
. Тогда 

 .
.
Следствие: если для некоторой функции  найдена какая-нибудь первообразная
найдена какая-нибудь первообразная  , то любая другая первообразная имеет вид
, то любая другая первообразная имеет вид  .
.
Определение. Если  есть первообразная функции
есть первообразная функции  , то выражение
, то выражение  называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается 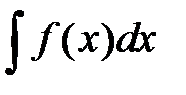 .
.
 – подынтегральная функция;
– подынтегральная функция;  – подынтегральное выражение.
– подынтегральное выражение.
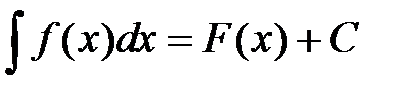 .
.
Теорема 2: Если функция  непрерывна на отрезке
непрерывна на отрезке 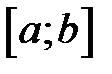 , то для этой функции существует первообразная на этом отрезке.
, то для этой функции существует первообразная на этом отрезке.
Свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции 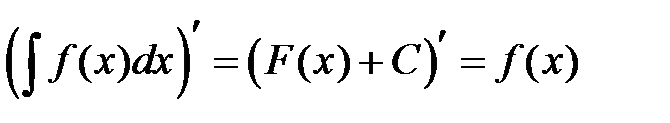 .
.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
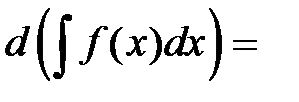
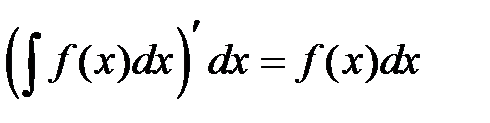 .
.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная. 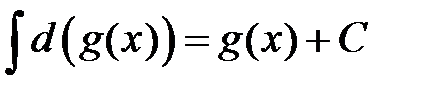 .
.
4. 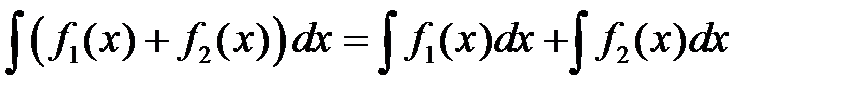 .
.
5.  .
.
6. Если 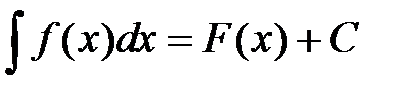 , то
, то
а)  ,
,
б)  ,
,
в)  .
.
Таблица интегралов
1.  ;
;
2.  ;
;
3.  ;
;
4. 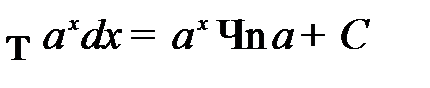 ;
;
5. 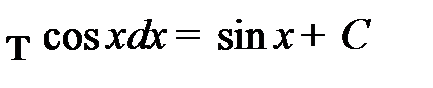 ;
;
6. 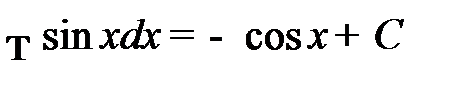 ;
;
7. 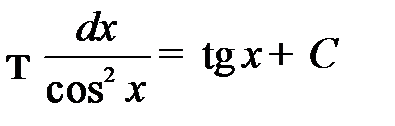 ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  .
.
Методы интегрирования
I. Интегрирование методом подстановки.
Заметим, что следующие равенства не зависят от того, как обозначается переменная 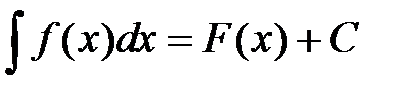
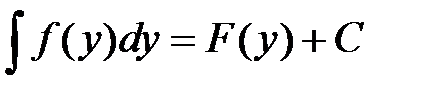
 .
.
Обобщение: 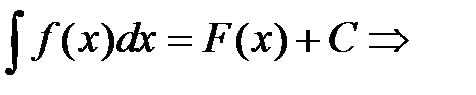

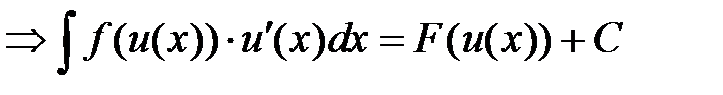 , что следует из правила дифференцирования сложной функции
, что следует из правила дифференцирования сложной функции  .
.
Часто метод подстановки применяется в другой форме. В этом случае переменную представляют как функцию вспомогательного аргумента. 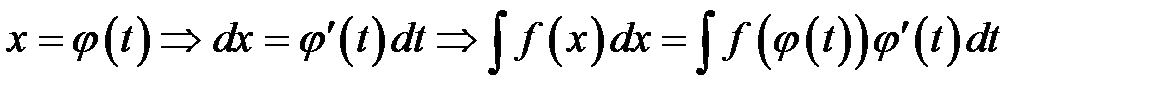 .
.
II. Интегрирование по частям.
Пусть  и
и  функции, имеющие непрерывные производные. Тогда
функции, имеющие непрерывные производные. Тогда 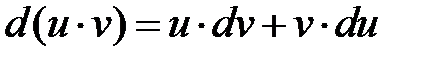 . Интегрируя это равенство, получим
. Интегрируя это равенство, получим 
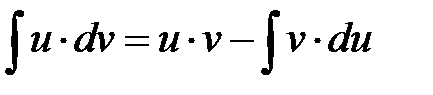 .
.
Интегрирование рациональных дробей.
I. Дроби правильные и неправильные. Выделение целой части.
Дробно-рациональной функцией называется функция вида  , где
, где  и
и 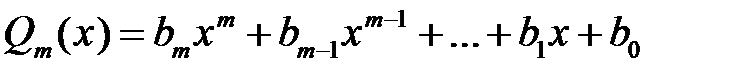 многочлены соответственно степени
многочлены соответственно степени  . Если
. Если  , то дробь называется правильной. В противном случае – неправильной. Для неправильной дроби нужно выполнить процедуру выделения целой части, т.е. представить данную неправильную дробь как сумму многочлена и правильной дроби
, то дробь называется правильной. В противном случае – неправильной. Для неправильной дроби нужно выполнить процедуру выделения целой части, т.е. представить данную неправильную дробь как сумму многочлена и правильной дроби 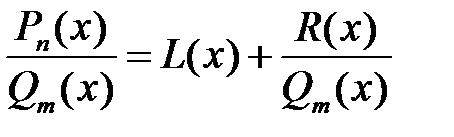 . Где
. Где  - частное и остаток деления числителя дроби на знаменатель.
- частное и остаток деления числителя дроби на знаменатель.
 .
.
Корнем многочлена  называется число
называется число 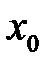 (действительное или комплексное), такое, что
(действительное или комплексное), такое, что  . При этом многочлен можно разложить на множители
. При этом многочлен можно разложить на множители  , где
, где
 – кратность корня
– кратность корня 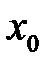 . Если
. Если 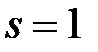 , то корень называется простым. В случае, если многочлен с действительными коэффициентами имеет комплексный корень, то комплексное число, сопряженное данному корню, также является корнем этого многочлена. Тогда в разложении многочлена на множители входит квадратный трехчлен с отрицательным дискриминантом
, то корень называется простым. В случае, если многочлен с действительными коэффициентами имеет комплексный корень, то комплексное число, сопряженное данному корню, также является корнем этого многочлена. Тогда в разложении многочлена на множители входит квадратный трехчлен с отрицательным дискриминантом  .
.
II. Знаменатель имеет простые действительные корни.
Теорема 1: Пусть  простой корень знаменателя дроби
простой корень знаменателя дроби  . Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей
. Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей  .
.
III. Знаменатель имеет действительные кратные корни.
Теорема 2: Пусть  корень знаменателя дроби
корень знаменателя дроби  кратности
кратности  . Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей
. Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей  .
.
Следствие: 
IV. Знаменатель имеет комплексные корни.
Теорема 3: Пусть два комплексных сопряженных числа  являются корнями знаменателя дроби
являются корнями знаменателя дроби  . Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей
. Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей  .
.
Интегрирование тригонометрических функций.
Вычисление неопределенных интегралов от функций рационально зависящих от  и
и  , то есть интегралов вида
, то есть интегралов вида  проводят с помощью универсальной тригонометрической подстановки. При этом выбирают новую переменную
проводят с помощью универсальной тригонометрической подстановки. При этом выбирают новую переменную 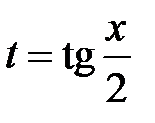 . В этом случае все подынтегральное выражение зависит от
. В этом случае все подынтегральное выражение зависит от  :
:  .
.
В некоторых случаях возможны более простые приемы вычисления интегралов.
Для вычисления интегралов вида  можно использовать
можно использовать
1) Подстановку  , если
, если 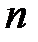 – положительное нечетное число;
– положительное нечетное число;
2) Подстановку  , если
, если  – положительное нечетное число;
– положительное нечетное число;
3) Формулы понижения степени  , если
, если 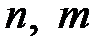 – неотрицательные четные числа;
– неотрицательные четные числа;
4) Подстановку  , если
, если  – четное отрицательное число;
– четное отрицательное число;
5) Тригонометрические формулы
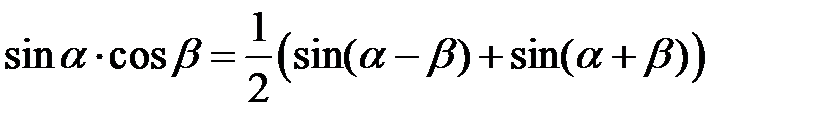 ,
,
 ,
,
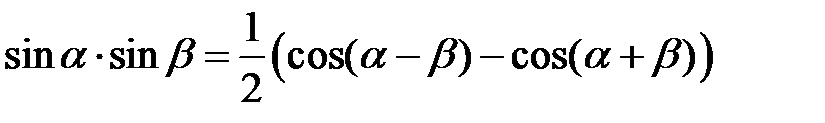 для интегралов вида
для интегралов вида 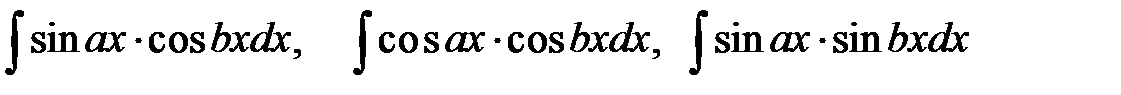 .
.
Определенный интеграл.
I. Задачи, приводящие к понятию определенного интеграла.
Задача 1 (задача о работе силы).
Пусть на прямолинейном участке  движется материальная точка под действие переменной силы
движется материальная точка под действие переменной силы 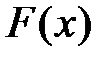 . Вычислить работу, производимую этой силой.
. Вычислить работу, производимую этой силой.
Разобьем отрезок  на
на  частей
частей 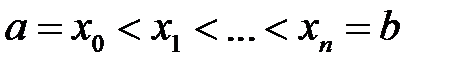 . Пусть
. Пусть  так велико, а разбиения
так велико, а разбиения  так малы, что на каждом из них сила
так малы, что на каждом из них сила 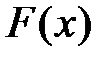 практически постоянна и равна
практически постоянна и равна  , где точка
, где точка 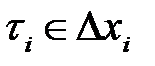 . Тогда на каждом участке разбиения
. Тогда на каждом участке разбиения  . Работа на всем отрезке
. Работа на всем отрезке  равна
равна  . Точное значение работы равно
. Точное значение работы равно  (
(  ).
).
Задача 2 (о площади криволинейной трапеции).
Пусть функция  непрерывна на отрезке
непрерывна на отрезке  . Найти площадь криволинейной трапеции, ограниченной графиком функции
. Найти площадь криволинейной трапеции, ограниченной графиком функции  , прямыми
, прямыми 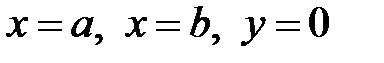 .
.
Разобьем отрезок  на
на  частей
частей 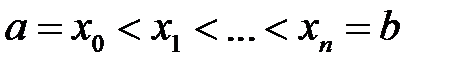 . Пусть
. Пусть  так велико, а разбиения
так велико, а разбиения  так малы, что на каждом из них
так малы, что на каждом из них  практически постоянна. Тогда на каждом участке разбиения площадь элементарной криволинейной трапеции равна площади прямоугольника
практически постоянна. Тогда на каждом участке разбиения площадь элементарной криволинейной трапеции равна площади прямоугольника  (точка
(точка 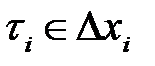 ). Площадь на всем отрезке
). Площадь на всем отрезке  равна
равна  . Точное значение
. Точное значение  (
(  ).
).
Определение:
Пусть функция  непрерывна на отрезке
непрерывна на отрезке  . Разобьем отрезок
. Разобьем отрезок  на
на  частей
частей 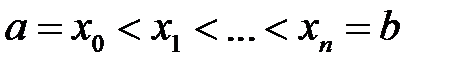 . Рассмотрим интегральную сумму
. Рассмотрим интегральную сумму  , где
, где  и
и 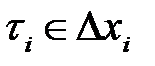 .
.
Если существует  (
(  )., то он называется определенный интеграл и обозначается
)., то он называется определенный интеграл и обозначается  .
.
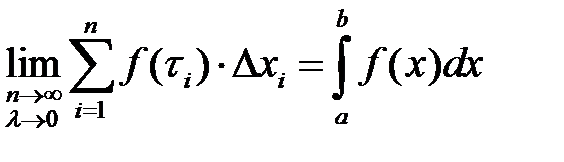 .
.
Можно доказать, что предел, а значит и интеграл не зависит от разбиения отрезка  на части и выбора точек
на части и выбора точек  .
.
В задаче 1: Работа 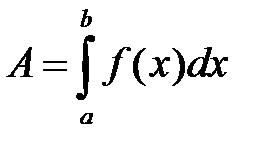 ; в задаче 2: площадь криволинейной трапеции
; в задаче 2: площадь криволинейной трапеции 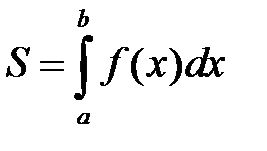 .
.
Популярное:
- A. Холодный двигатель не запускается или запускается плохо
- Agrale — бразильская фирма из Кашиас-ду-Сул, производящая небольшие грузовые автомобили, автобусы и сельскохозяйственную технику. Образована в 1962 году.
- D-технология построения чертежа. Типовые объемные тела: призма, цилиндр, конус, сфера, тор, клин. Построение тел выдавливанием и вращением. Разрезы, сечения.
- Exercise 2: Are these statements true or false? – Истинны или ложны данные высказывания?
- I. Если глагол в главном предложении имеет форму настоящего или будущего времени, то в придаточном предложении может употребляться любое время, которое требуется по смыслу.
- I.5. Киностилистика и монтаж
- II. Книги (по алфавиту авторов или названий)
- II.1.2. Глоссарий «Проблем киностилистики»
- II.2. Коррекция и реабилитация речевой патологии у детей, страдающих дизартрией
- III. Стабилизация исламского режима в 1980-е гг.
- Je suis Charlie de Gaule или как спецслужбы накачивают реальность энергией страха
- MAKE: утилита сопровождения программ

