Другие уравнения в целых числах.

⇐ ПредыдущаяСтр 7 из 14Следующая ⇒

Все описанные в предыдущей главе методы применимы для решения не только диофантовых уравнений второго порядка с двумя неизвестными, но и других уравнений в целых числах. К таким уравнениям относятся уравнения второго порядка с тремя и более переменными, уравнения более высокого, чем второго, порядка, уравнения, содержащие показательные и логарифмические функции, а также некоторые другие уравнения. Выбор нужного метода при решении подобного уравнения порой является определяющим условием для успешного решения задачи. Рассмотрим несколько примеров.

Уровень А:

Пример 1. Решить в целых числах уравнение

Решение. Преобразуем данное уравнение следующим образом:

⇔

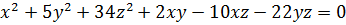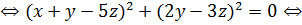
Ответ: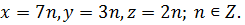

Пример 2. Найти все пары целых чисел , каждая из которых удовлетворяют уравнению

Решение. Ясно, что пара является решением данного уравнения. Предположим теперь, что хотя бы одно из чисел отлично от нуля. Имеем

при всех значениях . Так как 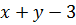— целое число, то возможны три варианта.

1. Если , то , нет решений.

2. Если , то 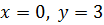, либо

3. Если , то , следовательно, .

Таким образом, решением данного уравнения будут служить следующие пары чисел:

Ответ:

Уровень В:

Пример 3. Найти все тройки простых чисел которые удовлетворяют равенству

Решение. Заметим сначала, что если тройка удовлетворяет условию задачи, то и для тройки данное равенство также выполняется. Предположим, что оба числа и нечетны. Тогда четно. Однако простое, значит, . Легко видеть, что равенство при натуральных выполняется лишь при 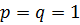, однако число 1 не является простым.

Итак, хотя бы одно из чисел четно (и, значит, равно 2). Если , то не является простым числом. Пусть . Заметим, что при — простое число, т.е. тройка удовлетворяет условию задачи.

Пусть 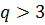. Так как простое нечетное, то при делении на 6 оно может давать остаток 1 или 5, тогда при делении на 6 дает остаток 1. Рассмотрим остатки от деления на 6 степеней двойки. Они периодически повторяются: . Если дает при делении на 6 остаток 1 или 5, то дает остаток 2. Следовательно, дает остаток 3 при делении на 6 и поэтому делится на 3. Это может быть только при . Однако ясно, что никакое 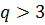не удовлетворяет равенству . Таким образом, решением задачи будут служить тройки

Ответ: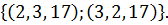

Пример 4. Найти все , при которых оба числа, и , являются целыми числами.

Решение. Пусть 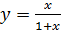– целое число. Тогда и

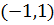где Решим последнее уравнение в целых числах. При или дробь лежит в интервале и не является целым числом. Перебирая остальные , находим, что решением уравнения являются , , 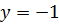и , т.е. ответом к задаче служит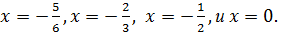

Ответ:

Уровень С:

Пример 6. Решить в натуральных числах уравнение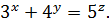

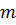Решение. Так как правая часть исходного уравнения при натуральных дает при делении на 4 остаток 1, то и левая часть этого уравнения должна давать такой же остаток при делении на 4, откуда следует, что четно. Пусть , где — натуральное число. Аналогично рассмотрим остатки обеих частей уравнения при делении на 3. Левая часть при всех натуральных и дает остаток 1, а дает остаток 1 только при четных , откуда следует, что , где - натуральное число. Тогда исходное уравнение можно переписать в виде , или .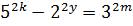

Разложим левую часть полученного уравнения по формуле разности квадратов. Имеем .

Так как разложение правой части на простые множители содержит только тройки, то каждая из скобок левой части должна быть неотрицательной степенью тройки. Поскольку разность чисел, стоящих в этих скобках, равна и не делится на 3, то это возможно только в случае, когда а . Отсюда , а

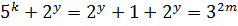или .

Еще раз применяя формулу разности квадратов, получаем

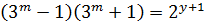Значит, оба сомножителя в левой части являются степенями двойки, отличающимися на 2. Следовательно, , а , откуда , а , т.е. 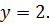Таким образом, единственным решением уравнения являются