Задачи, использующие делимость целых чисел.
Важную роль при решении задач на делимость играет основная теорема арифметики. Она утверждает, что каждое натуральное число  имеет единственное (с точностью до порядка множителей) разложение на простые множители
имеет единственное (с точностью до порядка множителей) разложение на простые множители

где  -попарно различные простые числа, а
-попарно различные простые числа, а  - натуральные числа. Данная форма записи называется каноническим разложением числа
- натуральные числа. Данная форма записи называется каноническим разложением числа  .
.
Отметим также некоторые признаки делимости, не имеющие широкого распространения.
1. Число делится на  тогда и только тогда, когда число, составленное из последних
тогда и только тогда, когда число, составленное из последних  цифр его десятичной записи, идущих в том же порядке, делится на
цифр его десятичной записи, идущих в том же порядке, делится на  .
.
2. Число делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9. Более того, любое натуральное число даёт при делении на 9 тот же остаток, что и сумма всех его цифр. Сказанное верно и для делимости на 3
3. Число делится на 11 тогда и только тогда, когда разность суммы цифр, стоящих на нечётных местах, считая справа в десятичной записи данного числа, и суммы цифр, стоящих на чётных местах в десятичной записи данного числа, делится на 11.
Некоторые задачи на делимость решаются путем перебора всевозможных остатков при делении на какое-либо натуральное число так, как это делалось при решении некоторых диофантовых уравнений. Рассмотрим несколько примеров.
Уровень А:
Пример 1. Определить сумму всех таких натуральных чисел  , для которых числа 5600 и 3024 делятся без остатка на
, для которых числа 5600 и 3024 делятся без остатка на  и
и  соответственно.
соответственно.
Решение. Разложим числа 5600 и 3024 на простые множители. Имеем:

Если число  делится на 5, то и число
делится на 5, то и число  также делится на 5. Но в этом случае число 3024 не может делиться на
также делится на 5. Но в этом случае число 3024 не может делиться на  , так как в его разложении на простые множители пятерки отсутствуют. Следовательно,
, так как в его разложении на простые множители пятерки отсутствуют. Следовательно,  не делится на 5. В этом случае
не делится на 5. В этом случае  является делителем числа
является делителем числа  . Все возможные варианты запишем в виде таблицы:
. Все возможные варианты запишем в виде таблицы:
Из чисел второй строки делителями числа  являются 6, 7, 9, 12 и 21. Соответствующие им значения
являются 6, 7, 9, 12 и 21. Соответствующие им значения  равны 1, 2, 4, 7 и 16. Их сумма равна 30.
равны 1, 2, 4, 7 и 16. Их сумма равна 30.
Ответ: 30.
Пример 2. Пусть 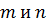 — натуральные числа, причем
— натуральные числа, причем  правильная несократимая дробь. На какие натуральные числа можно сократить дробь
правильная несократимая дробь. На какие натуральные числа можно сократить дробь  , если известно, что она сократима?
, если известно, что она сократима?
Решение. Пусть  — общий делитель чисел
— общий делитель чисел 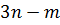 и
и  . Имеем следующую систему уравнений:
. Имеем следующую систему уравнений:

Если домножим первое уравнение этой системы на 2 и сложим со вторым, то получим уравнение  . Аналогично, умножив первое уравнение системы на 5, а второе на 3 и произведя вычитание, получим, что
. Аналогично, умножив первое уравнение системы на 5, а второе на 3 и произведя вычитание, получим, что  Запишем полученные равенства в виде системы:
Запишем полученные равенства в виде системы:

Рассмотрим несколько случаев.
Если  не делится на 11, то
не делится на 11, то  является общим делителем чисел
является общим делителем чисел 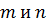 , что противоречит условию задачи. Если
, что противоречит условию задачи. Если  делится на 11, но
делится на 11, но  , тогда число - также будет являться общим делителем
, тогда число - также будет являться общим делителем 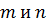 , что невозможно. И, наконец, если
, что невозможно. И, наконец, если  , то в качестве примера можно взять
, то в качестве примера можно взять 
Тогда дробь  , равную
, равную  , можно сократить на 11.
, можно сократить на 11.
Таким образом, если данная в условии задачи дробь сократима, то ее можно сократить только на число 11.
Ответ: на 11.
Пример 3. Найти все натуральные  , при которых число
, при которых число  делится нацело на 169.
делится нацело на 169.
Решение. Если данное число  делится на
делится на  , то оно делится и на 13. Поскольку число 52 делится на 13, то и произведение
, то оно делится и на 13. Поскольку число 52 делится на 13, то и произведение  также делится на 13. Поэтому хотя бы один из его сомножителей
также делится на 13. Поэтому хотя бы один из его сомножителей 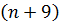 или
или  делится на 13, а так как
делится на 13, а так как  , то сразу оба числа
, то сразу оба числа 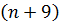 и
и  делятся на 13. Следовательно, их произведение делится на 169, а поскольку 52 не делится на 169, то сумма
делятся на 13. Следовательно, их произведение делится на 169, а поскольку 52 не делится на 169, то сумма  также не делится на 169.
также не делится на 169.
Ответ: таких чисел нет.
Уровень В:
Пример 4. Совокупность  состоит из различных натуральных чисел. Количество чисел в
состоит из различных натуральных чисел. Количество чисел в  больше семи. Наименьшее общее кратное всех чисел из
больше семи. Наименьшее общее кратное всех чисел из  равно 210. Для любых двух чисел из
равно 210. Для любых двух чисел из  их наибольший общий делитель больше единицы. Произведение всех чисел из
их наибольший общий делитель больше единицы. Произведение всех чисел из  делится на 1920 и не является квадратом никакого целого числа. Найти числа, из которых состоит
делится на 1920 и не является квадратом никакого целого числа. Найти числа, из которых состоит  .
.
Решение. Разложим числа 210 и 1920 на простые множители:

Так как произведение всех чисел из  делится на 1920,
делится на 1920,  должно содержать по крайней мере семь, чисел, имеющих в своём разложении на простые множители двойку. Среди делителей числа 210 таких чисел восемь:
должно содержать по крайней мере семь, чисел, имеющих в своём разложении на простые множители двойку. Среди делителей числа 210 таких чисел восемь:

Совокупность  не может состоять только из этих восьми чисел, так как тогда их произведение равно
не может состоять только из этих восьми чисел, так как тогда их произведение равно  и является полным квадратом. Но, согласно условию задачи, количество чисел в
и является полным квадратом. Но, согласно условию задачи, количество чисел в  больше семи. А это означает, что в
больше семи. А это означает, что в  присутствует, по крайней мере, одно число, не входящее в данный список, т.е. не содержащее в своём разложении двойку. Следовательно, число 2 не может входить в
присутствует, по крайней мере, одно число, не входящее в данный список, т.е. не содержащее в своём разложении двойку. Следовательно, число 2 не может входить в  , так как иначе
, так как иначе  содержало бы два взаимно простых числа, что противоречит одному из условий задачи. Кроме того, ясно, что число, содержащееся в
содержало бы два взаимно простых числа, что противоречит одному из условий задачи. Кроме того, ясно, что число, содержащееся в 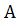 и не входящее в список, - это
и не входящее в список, - это  , так как любое другое такое число будет взаимно просто с одним из чисел списка - например, число
, так как любое другое такое число будет взаимно просто с одним из чисел списка - например, число  взаимно просто с числом
взаимно просто с числом  . Значит, совокупность
. Значит, совокупность  состоит из следующих восьми чисел:
состоит из следующих восьми чисел:

Ответ: 
Пример 5. Натуральные числа  , взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2835 и 2646 делятся без остатка на
, взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2835 и 2646 делятся без остатка на  соответственно. Найти числа
соответственно. Найти числа  , если известно, что при указанных условиях сумма
, если известно, что при указанных условиях сумма  максимальна.
максимальна.
Решение. Пусть  - целое число, являющееся знаменателем данной геометрической прогрессии. Тогда
- целое число, являющееся знаменателем данной геометрической прогрессии. Тогда  . Разложим числа 2835 и 2646 на простые множители. Имеем:
. Разложим числа 2835 и 2646 на простые множители. Имеем:

Так как первое из этих чисел делится на  , а второе на
, а второе на  , то
, то  может принимать только одно из трех значений:
может принимать только одно из трех значений:  .
.
Если  , то число 2835 должно делиться на
, то число 2835 должно делиться на  следовательно,
следовательно, 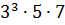 должно делиться на
должно делиться на  . Аналогично 2646 делится на
. Аналогично 2646 делится на  , т.е.
, т.е.  делится на
делится на  . Так как при этих условиях
. Так как при этих условиях  должно быть максимальным (при фиксированном
должно быть максимальным (при фиксированном  сумма
сумма  максимальна тогда и только тогда, когда максимально
максимальна тогда и только тогда, когда максимально  ), то
), то  есть наибольший общий делитель (НОД) чисел
есть наибольший общий делитель (НОД) чисел 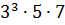 и
и  т.е.
т.е.  В этом случае
В этом случае  и
и 
Если  , то 2835 делится на
, то 2835 делится на  , а 2646 делится на
, а 2646 делится на  , откуда непосредственно вы3текает, что
, откуда непосредственно вы3текает, что  . При этом
. При этом  И, наконец, при
И, наконец, при  имеем, что
имеем, что  . В этом случае
. В этом случае  Таким образом, сумма
Таким образом, сумма  максимальна при
максимальна при  и ответом к задаче будут служить числа
и ответом к задаче будут служить числа 
Ответ: 
Уровень С:
Пример 6. Найти все пары пятизначных чисел 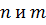 такое, что число
такое, что число  , полученное приписыванием десятичной записи числа
, полученное приписыванием десятичной записи числа 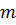 после десятичной записи числа
после десятичной записи числа  , делится на
, делится на  .
.
Решение. Согласно условию задачи число  делится на
делится на  , следовательно, это число делится на
, следовательно, это число делится на  . Так как
. Так как  делится на
делится на  , то и
, то и 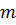 делится на
делится на  . Пусть
. Пусть  . Тогда число
. Тогда число  должно делиться на
должно делиться на  число
число  должно делиться на
должно делиться на  . Сразу заметим, что число
. Сразу заметим, что число  не может превосходить 9, так как иначе при умножении на
не может превосходить 9, так как иначе при умножении на  пятизначного числа получим шестизначное (или состоящее из большого количества знаков) число.
пятизначного числа получим шестизначное (или состоящее из большого количества знаков) число.
Далее, число  должно делиться на
должно делиться на  , следовательно, это число делится на
, следовательно, это число делится на  . Отсюда вытекает, что и число
. Отсюда вытекает, что и число  делится на
делится на  . С учетом вышесказанного
. С учетом вышесказанного  может принимать одно из следующих пяти значений:
может принимать одно из следующих пяти значений:  ,
,  ,
,  ,
,  ,
,  . Тогда
. Тогда  делится на
делится на  . Пусть
. Пусть  Обратим внимание, что число
Обратим внимание, что число 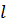 не может быть равно единице. Действительно, в этом случае
не может быть равно единице. Действительно, в этом случае  не является пятизначным числом.
не является пятизначным числом.
Рассмотрим каждый случай в отдельности. Пусть сначала  . тогда должно быть выполнено равенство
. тогда должно быть выполнено равенство 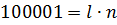 . При этом
. При этом 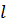 не может превосходить 10 (действительно,
не может превосходить 10 (действительно,  является четырехзначным числом). Но у числа
является четырехзначным числом). Но у числа  нет делителей, лежащих в интервале от 2 до 10. Таким образом, данный случай невозможен. Пусть теперь
нет делителей, лежащих в интервале от 2 до 10. Таким образом, данный случай невозможен. Пусть теперь  . В этом случае имеем, что
. В этом случае имеем, что  . По тем же соображениям
. По тем же соображениям 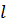 здесь не превосходит 5. Из чисел 2, 3, 4 делителем 50001 является число
здесь не превосходит 5. Из чисел 2, 3, 4 делителем 50001 является число  . При этом
. При этом  и
и  .
.
Если  , равенство
, равенство  примет вид
примет вид  . Здесь имеет только одно возможное значение
. Здесь имеет только одно возможное значение  это
это  (при
(при  число
число  уже не будет пятизначным). Ясно, что
уже не будет пятизначным). Ясно, что  не является делителем 25001. Аналогично, случаи
не является делителем 25001. Аналогично, случаи  и
и  также являются невозможным. Действительно, при
также являются невозможным. Действительно, при  получаем равенство 20001=
получаем равенство 20001=  , а при
, а при  равенство 12501=
равенство 12501=  . Как легко видеть, нет таких натуральных
. Как легко видеть, нет таких натуральных 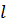 , чтобы
, чтобы  в этих равенствах было пятизначным числом.
в этих равенствах было пятизначным числом.
Таким образом, ответом к задаче будут служить  и
и  .
.
Ответ:  ,
,  .
.
Пример 7. Существует ли степень двойки, из которой перестановкой цифр можно получить другой степень двойки?
Решение.
Два числа, отличающиеся лишь порядком цифр, дают одинаковые остатки при делении на 9. Это следует из того факта, что число дает такой же остаток при делении на 9, что и сумма все его цифр. Выясним, какие остатки при делении на 9 могут давать числа вида 
| Степень числа 2:
| 
| 
| 
| 
| 
| 
| 
|
| Остаток степени при делении на 9:
|
|
|
|
|
|
|
|
Докажем, что последовательность остатков при делении на 9 степеней двойки 2, 4, 8, 7, 5, 1, 2, … периодична с периодом 6. Действительно,
 делится на 9. Предположим, что две степени двойки отличаются только лишь порядком цифр, тогда они дают одинаковый остаток при делении на 9 и отличаются не менее чем в
делится на 9. Предположим, что две степени двойки отличаются только лишь порядком цифр, тогда они дают одинаковый остаток при делении на 9 и отличаются не менее чем в  раза, т.е. в них разное количество цифр. Получаем противоречие.
раза, т.е. в них разное количество цифр. Получаем противоречие.
Ответ: Не существует.
В отличие от уже рассмотренных текстовых задач в этом параграфе, для следующих задач свойства делимости имеют определяющее значение. В процессе решения таких задач необходимо следить за целочисленностью всех переменных, которые должны быть таковыми по смыслу задачи. Конечно, при этом остаются в силе и другие уже рассмотренные методы решения задач в целых числах. Рассмотрим несколько примеров.
Уровень А:
Пример 8. За 2005 год число книг в фонде библиотеки поселка увеличилось на 0, 4%, а за 2006 год -на 0, 8%, оставшись при этом меньше 50 тысяч. На сколько книг увеличивался фонд библиотека поселка за 2006 год?
Решение. Пусть  - число книг в библиотеке в начале 2005 года. Тогда в конце 2005 года в библиотеке было
- число книг в библиотеке в начале 2005 года. Тогда в конце 2005 года в библиотеке было  , а в конце 2006 года -
, а в конце 2006 года -  .Так как последнее число является целым, а каждое из чисел 125 и 250 взаимно просто с каждым из чисел 126 и 251, то x делится без остатка на
.Так как последнее число является целым, а каждое из чисел 125 и 250 взаимно просто с каждым из чисел 126 и 251, то x делится без остатка на  . Поскольку x при этом не превосходит 50000, то x=31250. Тогда за 2006 год фонд библиотеки увеличился на
. Поскольку x при этом не превосходит 50000, то x=31250. Тогда за 2006 год фонд библиотеки увеличился на 
Ответ: на 251 книгу.
Пример 9. На заводе было несколько одинаковых прессов, штампующих детали, и завод выпускал 6480 деталей в день. После реконструкции все прессы заменили на более производительные, но также одинаковые, а их число увеличилось на 3. Завод стал выпускать в день 11 200 деталей. Сколько прессов было первоначально?
Решение. Разложим числа 6480 и 11 200 на простые множители  .
.
Пусть  - количество прессов, которое было на заводе первоначально. Тогда
- количество прессов, которое было на заводе первоначально. Тогда  - количество прессов, которое стало после реконструкции. Так как каждый пресс выпускает в день целое число деталей, то 6480 должно делиться на n, а 11200- на
- количество прессов, которое стало после реконструкции. Так как каждый пресс выпускает в день целое число деталей, то 6480 должно делиться на n, а 11200- на  . При этом n не может делиться на 3, так как тогда бы и
. При этом n не может делиться на 3, так как тогда бы и  делилось на 3, а в разложении числа 11200 на простые множители тройки отсутствуют. Значит,
делилось на 3, а в разложении числа 11200 на простые множители тройки отсутствуют. Значит,  является делителем числа
является делителем числа  , т.е. может принять одно из следующих значений:
, т.е. может принять одно из следующих значений:
2, 4, 5, 8, 10, 16, 20, 40, 80.
Тогда  принимает, соответственно, значения
принимает, соответственно, значения
5, 7, 8, 11, 13, 19, 23, 43, 83.
Ясно, что всем условиям делимости удовлетворяют  В случае
В случае  производительность каждого пресса до реконструкции равна 3240 деталей в день, а после реконструкции-2240 деталей в день, что противоречит условию задачи. В случае
производительность каждого пресса до реконструкции равна 3240 деталей в день, а после реконструкции-2240 деталей в день, что противоречит условию задачи. В случае  производительность каждого пресса до реконструкции равна 1620 деталей в день, а после реконструкции-1600 деталей в день, что также противоречит условию задачи. И, наконец, в случае
производительность каждого пресса до реконструкции равна 1620 деталей в день, а после реконструкции-1600 деталей в день, что также противоречит условию задачи. И, наконец, в случае  производительность каждого пресса до реконструкции равна 1296 деталей в день, а после реконструкции – 1400 деталей в день, что не противоречит условию задачи.
производительность каждого пресса до реконструкции равна 1296 деталей в день, а после реконструкции – 1400 деталей в день, что не противоречит условию задачи.
Ответ: 5 прессов.
Уровень В:
Пример 10. Брокерская фирма выставила на торги акции двух компаний: нефтяной компании – по 100 долларов за акцию и газовой компании – по 65 долларов 60 центов за акцию. Всего было 200 акций. Все акции газовой компании были проданы, а часть акций нефтяной компании осталась непроданной. Общая сумма выручки оказалась равной 13120 долларов. Найти сумму выручки, полученной за акции газовой компании.
Решение.
Пусть  - количество проданных акций нефтяной и газовой компаний соответственно. Согласно условию задачи получаем уравнение:
- количество проданных акций нефтяной и газовой компаний соответственно. Согласно условию задачи получаем уравнение:

Так как число  является целым, а число 125 и 82 взаимно простые, то
является целым, а число 125 и 82 взаимно простые, то  должно делиться на 82 без остатка. Следовательно,
должно делиться на 82 без остатка. Следовательно,  , так как иначе число
, так как иначе число 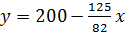 будет отрицательной. Таким образом, выручка от продажи акций газовой компании составляет
будет отрицательной. Таким образом, выручка от продажи акций газовой компании составляет  долларов.
долларов.
Ответ: 4920 долларов.
Пример 11. На цехе имелось  одинаковых станков, которые, работая вместе, вытачивали в день 5850 деталей. После реконструкции число производимых в день каждым станком деталей возросло на 20%. Это позволило, по крайней мере, без сокращения общего объема продукции цеха уменьшить число станков максимум на четыре. Найти
одинаковых станков, которые, работая вместе, вытачивали в день 5850 деталей. После реконструкции число производимых в день каждым станком деталей возросло на 20%. Это позволило, по крайней мере, без сокращения общего объема продукции цеха уменьшить число станков максимум на четыре. Найти  .
.
Решение.
Пусть  - количество деталей, которые вытачивал в день каждый станок до реконструкции. Тогда, согласно условиям задачи, имеем следующую систему:
- количество деталей, которые вытачивал в день каждый станок до реконструкции. Тогда, согласно условиям задачи, имеем следующую систему:

Так как  целое число, то
целое число, то  Разложим теперь число 5850 на простые множители:
Разложим теперь число 5850 на простые множители:  . Поскольку
. Поскольку  является делителем числа 5850. то
является делителем числа 5850. то  или
или  . Если
. Если  , то
, то  и
и  целое число. Таким образом, в цехе до реконструкции было 26 станков.
целое число. Таким образом, в цехе до реконструкции было 26 станков.
Ответ: 26 станков.
Уровень С:
Пример 12. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала 5%, затем 12%, потом  и, наконец, 12, 5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на
и, наконец, 12, 5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на  Определите срок хранения вклада.
Определите срок хранения вклада.
Решение. Пусть x, y, z и -число месяцев, которое вклад находился под действием каждой из перечисленных процентных ставок соответственно. Имеем уравнение:

и после преобразований
 .
.
Используя теорему об единственности разложения любого натурального числа на простые множите, получим систему:

Так как  - натуральные числа, из последнего уравнения немедленно следует, что
- натуральные числа, из последнего уравнения немедленно следует, что  . Далее не составляет труда найти, что
. Далее не составляет труда найти, что  и
и  . Таким образом, общее число месяцев, которое вклад находился в банке, есть
. Таким образом, общее число месяцев, которое вклад находился в банке, есть  .
.
Ответ: 7 месяцев.
Пример 13. Каждый из трех брокеров имел в начале дня акции каждого из видов  общим число 11, 21 и 29 штук соответственно. Цены на акции в течение всего дня не менялись, причем цена одной акции вида А больше цены одной акции вида В. К концу дня брокерам удалось продать все свои акции, выручив от продажи по 4402 рубля каждый. Определить цену продажи одной акции видов А и В.
общим число 11, 21 и 29 штук соответственно. Цены на акции в течение всего дня не менялись, причем цена одной акции вида А больше цены одной акции вида В. К концу дня брокерам удалось продать все свои акции, выручив от продажи по 4402 рубля каждый. Определить цену продажи одной акции видов А и В.
Решение.
Обозначим через  количество акций вида
количество акций вида  в начале дня у первого, второго и третьего брокеров соответственно, а через
в начале дня у первого, второго и третьего брокеров соответственно, а через  - цены на акции видов
- цены на акции видов  . Согласно условиям задачи имеем следующую систему:
. Согласно условиям задачи имеем следующую систему:
 :
: 
Вычтем третье уравнение из первого и третье из второго.
Имеем:

Последнее равенство было получено делением двух уравнений с однородным выполнением условий  Далее, так как
Далее, так как  и
и  , то
, то  (поскольку из полученного равенства следует, что
(поскольку из полученного равенства следует, что  делится на 9) и, значит,
делится на 9) и, значит,  и
и  . Тогда
. Тогда  и
и  . Возвращаясь к исходной системе находим, что
. Возвращаясь к исходной системе находим, что 
Ответ: 426 рублей и 142 рубля.
Задачи для самостоятельного решения.
Уровень А:
1. Существует ли такое натуральное число  , что число
, что число  делится нацело на 2005? 2. Доказать, что
делится нацело на 2005? 2. Доказать, что  не делятся на 121 ни при каком целом
не делятся на 121 ни при каком целом 
2. Определить сумму всех таких натуральных чисел  , для которых числа 3920 и 4320 делятся без остатка на
, для которых числа 3920 и 4320 делятся без остатка на  и
и  соответственно.
соответственно.
3. Пусть 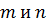 –натуральные числа, причем
–натуральные числа, причем  - правильная несократимая дробь. На какие натуральные числа можно сократить дробь
- правильная несократимая дробь. На какие натуральные числа можно сократить дробь  если известно, что она сократима?
если известно, что она сократима?
4. Среди учащихся старших классов провели опрос: кто любит волейбол, а кто баскетбол. Оказалось, что 52% любителей волейбола любят и баскетбол, а 65% любителей баскетбола любят и волейбол. Зато 36% всех опрошенных не любят ни волейбол, ни баскетбол. Каким при этих условиях могло быть наименьшее число опрошенных?
5. На фабрике несколько одинаковых поточных линий вместе выпускали в день 15000 банок консервов. После реконструкции все поточные линии заменили на более производительные, но также одинаковые, а их количество увеличилось на 5. Фабрика стала выпускать 33792 банки в день. Сколько поточных линий было первоначально?
Уровень В:
6. Доказать, что для любого простого числа  число
число  делится на 2880.
делится на 2880.
7. Доказать, что если сумма целых чисел делится на 6, то и сумма кубов этих же чисел делится на 6.
8. Найти все простые числа вида  , где -натуральное число.
, где -натуральное число.
9. Известно, что натуральное трехзначное число  делится нацело на 37. Должны ли числа
делится нацело на 37. Должны ли числа  и
и  также делиться нацело на 37?
также делиться нацело на 37?
10. Каждое из целых чисел  не делится на три. Доказать, что число
не делится на три. Доказать, что число  делится на три.
делится на три.
11. Доказать, что сумма кубов трех последовательных натуральных числе делится на 9.
12. Интервалы движения морских катеров по трём маршрутам, начинающимся на общей пристани, составляют 30, 36 и 45 минут соответственно. Сколько раз с 7 часов 40 минут до 17 часов 35 минут того же дня на этой пристани одновременно встречаются катера всех трёх маршрутов, если одна из таких встреч происходит в 11 часов 15 минут?
Уровень С:
14. Доказать, что натуральное число является полным квадратом тогда и только тогда, когда него нечетное число натуральных делителей.
15. Доказать, что при любом натуральном  сумма цифр числа
сумма цифр числа  не меньше 19.
не меньше 19.
16. Техническая реконструкция предприятия была проведена в четыре этапа. Каждый из этапов продолжался целое число месяцев и сопровождался падением производства. Ежемесячное падение производства составило на первом этапе 4%, на втором -  , на третьем -
, на третьем - 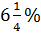 и на четвертом -
и на четвертом -  в месяц. По окончании реконструкции первоначальный объем производства на предприятии сократился на 37%. Определить продолжительность периода реконструкции.
в месяц. По окончании реконструкции первоначальный объем производства на предприятии сократился на 37%. Определить продолжительность периода реконструкции.
17. Численность населения города, не превышавшая 50 тыс. человек, за 2005 год сократилась на 1, 2%, а за 2006 год - на 2, 4%. На сколько человек сократилась численность населения города за 2006 год?
Популярное:
- I I. Цели, задачи, результаты выполнения индивидуального проекта
- III. Задачи, решаемые организацией с помощью ИСУ и ИТУ.
- Анализ использования основных фондов: задачи, объекты, этапы, источники информации, основные показатели.
- Анализ финансового состояния организации: задачи, методы, виды, последовательность, информационная база.
- Анализ финансовых результатов: задачи, объекты, этапы, источники информации, основные показатели.
- Виды, задачи, формы организации делопроизводства в органах внутренних дел. Субъекты делопроизводства в ОВД и их обязанности
- Глава 1. Основные типы уравнений в целых числах.
- Глава 1. Предмет, задачи, принципы и методы психологии
- Дошкольная педагогика: предмет, категории, задачи, источники, основные этапы в развитии дошкольной педагогики. Связь дошкольной педагогики с другими науками.
- Другие уравнения в целых числах.
- Задачи, адресаты и особенности интернационального развития персонала
- Задачи, аналогичные задачам С6 из ЕГЭ.

