Линейные уравнения с любым числом неизвестных.
Рассмотрим уравнение вида
 , (2.1)
, (2.1)
где  натуральное число, больше 1. Будем предполагать, что все коэффициенты
натуральное число, больше 1. Будем предполагать, что все коэффициенты  - различные натуральные числа (если
- различные натуральные числа (если  - отрицательное, то можно взять за коэффициент его абсолютную величину, изменив знак у неизвестного; если два коэффициента равны, например,
- отрицательное, то можно взять за коэффициент его абсолютную величину, изменив знак у неизвестного; если два коэффициента равны, например,  , то можно положить
, то можно положить  ).
).
Одно из них, например,  , есть наибольшим, в частности,
, есть наибольшим, в частности,  . Предположим, что число
. Предположим, что число  при делении на
при делении на 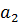 дает в частности натуральное число k и в остатке
дает в частности натуральное число k и в остатке 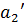 , так что
, так что  ,
,  (по теореме о делении с остатком).
(по теореме о делении с остатком).
Примем  ,
,  ,
,  . Тогда
. Тогда  +
+  и уравнение (3.1) перейдет в уравнение
и уравнение (3.1) перейдет в уравнение  (2.2)
(2.2)
Если примем  ,
,  , то из каждого решения уравнения (2.1) в целых числах получим решение в целых числах уравнения (2.2). Обратно, если положим
, то из каждого решения уравнения (2.1) в целых числах получим решение в целых числах уравнения (2.2). Обратно, если положим  ,
,  то из каждого решения в целых числах уравнения (2.2) получим решение в целых числах уравнения (2.1).
то из каждого решения в целых числах уравнения (2.2) получим решение в целых числах уравнения (2.1).
Таким образом, решение уравнения (2.1) в целых числах сводится к решению в целых числах уравнения (2.2), в котором наибольший из коэффициентов при неизвестных (учитывая, что 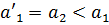 ) меньше, чем наибольший из коэффициентов при неизвестных в уравнение (2.1). Далее, аналогичным образом из уравнения (2.2) можно получить уравнение, в котором наибольший из коэффициентов будет меньше, чем наибольший из коэффициентов (2.2) и т.д.
) меньше, чем наибольший из коэффициентов при неизвестных в уравнение (2.1). Далее, аналогичным образом из уравнения (2.2) можно получить уравнение, в котором наибольший из коэффициентов будет меньше, чем наибольший из коэффициентов (2.2) и т.д.
Т.к. последовательность убывающих натуральных чисел не может быть бесконечной, то, пользуясь указанным приемом, придем либо к уравнению с одним неизвестным, решение которого не вызывает затруднений, либо к уравнению, в котором все коэффициенты при неизвестных равны, например, к уравнению  . Из этого уравнения следует, что свободный член
. Из этого уравнения следует, что свободный член  будет делиться на
будет делиться на  . Если бы это условие не выполнялось, то тогда уравнение это, а, следовательно, и уравнение (2.1) не имело бы решений в целых числах. Если
. Если бы это условие не выполнялось, то тогда уравнение это, а, следовательно, и уравнение (2.1) не имело бы решений в целых числах. Если  при делении на
при делении на  дает в частности целое
дает в частности целое  , то получаем уравнение
, то получаем уравнение  все решения которого в целых числах находим, полагая
все решения которого в целых числах находим, полагая  равными любым целым числам и принимая
равными любым целым числам и принимая  .
.
На практике, при объяснении целочисленных решений уравнения (2.1), указанный прием применяется до тех пор, пока не получается уравнение, в котором хотя бы при одном неизвестном будет коэффициент, равный единице.
Пример: Решить уравнение 
Принимая  , получаем уравнение
, получаем уравнение 
10-наибольшее, 10=7·1+3. Тогда  , или
, или  . Пусть
. Пусть  , тогда получим
, тогда получим  Теперь 7- наибольшее, 7=6·1+1. Тогда
Теперь 7- наибольшее, 7=6·1+1. Тогда  или
или  Пусть
Пусть  тогда получаем
тогда получаем 
Все решения в целых числах  этого уравнения получаем, если для
этого уравнения получаем, если для 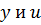 будем назначать любые целые числа и примем
будем назначать любые целые числа и примем  . А так как
. А так как  , то имеем
, то имеем  и далее, так как
и далее, так как  и
и  , то находим
, то находим 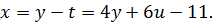
Все решения исходного уравнения в целых числах  содержится в формулах
содержится в формулах 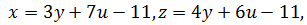
где 
Например,  .
.
Легко показать, что если уравнение 3.1 имеет решение в целых числах, то таких решений (в случае  ) оно имеет бесконечное множество.
) оно имеет бесконечное множество.
Действительно, если существует целые числа  такие, что
такие, что  то полагая
то полагая  а
а  , где
, где  - произвольные целые числа, получаем целые числа
- произвольные целые числа, получаем целые числа 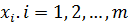 , удовлетворяющие уравнению (2.1).
, удовлетворяющие уравнению (2.1).
Теорема 2.1. Если  и
и  – целые числа, причем среди чисел
– целые числа, причем среди чисел  , по крайней мере одно отлично от нуля, то для разрешимости уравнения (3.1) в целых числах
, по крайней мере одно отлично от нуля, то для разрешимости уравнения (3.1) в целых числах  , необходимо и достаточно, чтобы свободный член
, необходимо и достаточно, чтобы свободный член  - делился на НОД чисел
- делился на НОД чисел  [12].
[12].
Уравнения второй степени с двумя неизвестными.
Можно легко указать примеры уравнений второй степени с двумя неизвестными и с целыми коэффициентами, которые не имеют решений в целых числах, например, уравнение  или уравнение
или уравнение  . Легко также указать пример уравнения, умеющего конечное число решений в целых числах. Например, уравнение
. Легко также указать пример уравнения, умеющего конечное число решений в целых числах. Например, уравнение  имеет только шестнадцать решений в целых числах, именно:
имеет только шестнадцать решений в целых числах, именно: 


 .
.
Легко исследовать для каких целых чисел  уравнение
уравнение

имеет решение в целых числах  .
.
Теорема 3.1. Уравнение (3.1) имеет по крайней мере одно решение в целых числах  тогда и только тогда, когда число
тогда и только тогда, когда число  при делении на 4 не дает в остатке 2 [12].
при делении на 4 не дает в остатке 2 [12].
Доказательство.
Необходимость. Если существуют целые числа  такие, что
такие, что  и если оба числа
и если оба числа  - четные, то, очевидно, числа
- четные, то, очевидно, числа  делятся на 4, и, следовательно, их разность
делятся на 4, и, следовательно, их разность  делится на 4.
делится на 4.
Если какое-нибудь одно из чисел  четное, а другое нечетное, то число
четное, а другое нечетное, то число  , а значит и число
, а значит и число  нечетное.
нечетное.
Наконец, если оба числа  - нечетные, то, поскольку квадрат нечетного числа при делении на 4 дает в остатке 1, заключаем, что число
- нечетные, то, поскольку квадрат нечетного числа при делении на 4 дает в остатке 1, заключаем, что число  , а значит и число
, а значит и число  делится на 4. Итак, ни в одном случае (когда наше уравнение (3.1) разрешимо в целых числах
делится на 4. Итак, ни в одном случае (когда наше уравнение (3.1) разрешимо в целых числах  ) число
) число  при делении на 4 не дает
при делении на 4 не дает  в остатке 2.
в остатке 2.
Достаточность. Предположим теперь, что целое число  при делении на 4 не дает в остатке 2. Тогда, если
при делении на 4 не дает в остатке 2. Тогда, если  - четное число, то оно делится на 4 и число
- четное число, то оно делится на 4 и число  – целое. Таким образом, числа
– целое. Таким образом, числа  являются целыми и, как легко проверить, удовлетворяют нашему уравнению.
являются целыми и, как легко проверить, удовлетворяют нашему уравнению.
Если же число  - нечетное, то имеем
- нечетное, то имеем  , гдe
, гдe 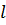 -целое число. Тогда числа
-целое число. Тогда числа  и
и  являются целыми и, как легко проверить, удовлетворяют уравнению (3.1).
являются целыми и, как легко проверить, удовлетворяют уравнению (3.1).
Теорема 3.2. Для каждого целого числа  уравнение (3.1) имеет лишь конечное
уравнение (3.1) имеет лишь конечное  число решений в целых числах
число решений в целых числах  .
.
Доказательство.
Достаточно доказать для натуральных  и для решений в натуральных числах
и для решений в натуральных числах  . Если натуральное число
. Если натуральное число  удовлетворяют уравнению
удовлетворяют уравнению  , где -натуральное число, то
, где -натуральное число, то  , откуда
, откуда 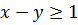 и имеем
и имеем  , что дает
, что дает  и следовательно,
и следовательно,  и
и  ; но число систем натуральных чисел
; но число систем натуральных чисел  удовлетворяющих двум последним неравенствам, равно, очевидно,
удовлетворяющих двум последним неравенствам, равно, очевидно,  и следовательно, является конечным.
и следовательно, является конечным.
Труднее исследовать вопрос, для каких натуральных  уравнение
уравнение  (3.2)
(3.2)
имеет хотя бы одно решение в целых числах  .
.
Теорема 3.3. Уравнение (3.2) имеет по крайней мере одно решение в целых числах  тогда и только тогда, когда частное от деления натурального числа
тогда и только тогда, когда частное от деления натурального числа  на наибольший квадрат не имеет не одного натурального делителя, который при делении на 4 давал бы в остатке 3.
на наибольший квадрат не имеет не одного натурального делителя, который при делении на 4 давал бы в остатке 3.
Поэтому, например, уравнение  разрешимо в целых числах
разрешимо в целых числах  . для
. для  =1, 2, 3, 4, 6, 8, 9, 10, но неразрешимо для
=1, 2, 3, 4, 6, 8, 9, 10, но неразрешимо для  .
.
Разумеется, для каждого целого числа  уравнение (3.2) имеет конечное
уравнение (3.2) имеет конечное  число решений в целых числах
число решений в целых числах  .
.
Еще труднее установить необходимое и достаточное условие того, чтобы для данного натурального числа  уравнение (3.2) имело бы по крайней мере одно решение в натуральных числах
уравнение (3.2) имело бы по крайней мере одно решение в натуральных числах  .
.
Теорема 3.4. Для каждого данного натурального числа  уравнение (3.2) имеет по крайней мере одно решение в натуральных числах
уравнение (3.2) имеет по крайней мере одно решение в натуральных числах  тогда и только тогда, когда:
тогда и только тогда, когда:
1) уравнение (3.2) разрешимо в целых числах  ;
;
2) либо число  имеет хотя бы один просто делитель, дающий при делении на 4 остаток 1, либо чтобы показатель наивысшей степени числа 2, делящей число
имеет хотя бы один просто делитель, дающий при делении на 4 остаток 1, либо чтобы показатель наивысшей степени числа 2, делящей число  , был нечетный.
, был нечетный.
Например, это уравнение (3.2) разрешимо в натуральных  для
для  , но неразрешимо в этих числах для
, но неразрешимо в этих числах для 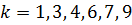 . Отсюда легко следует:
. Отсюда легко следует:
Теорема 3.5. Для того чтобы уравнение  , где
, где  - натуральное число, имело хотя бы одно решение в натуральных числах
- натуральное число, имело хотя бы одно решение в натуральных числах  необходимо и достаточно, чтобы число
необходимо и достаточно, чтобы число  имело по меньшей мере один простой делитель вида
имело по меньшей мере один простой делитель вида  , где
, где  - целое число.
- целое число.
Замечание 3.1. В этом состоит необходимое и достаточное условие существования (хотя бы одного) пифагорова треугольника с гипотенузой  .
.
Замечание 3.2. Легко доказать, что уравнение

имеет для каждого натурального  одно и только одно решение в натуральных числах
одно и только одно решение в натуральных числах  .
.
Если уравнение  , где
, где  - многочлен с целыми коэффициентами, имеет решение в целых числах
- многочлен с целыми коэффициентами, имеет решение в целых числах  , то, очевидно, для каждого натурального числа
, то, очевидно, для каждого натурального числа 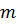 существуют целые числа
существуют целые числа  , при которых число
, при которых число  делится на
делится на 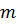 . Отсюда следует, что если существует натуральное число
. Отсюда следует, что если существует натуральное число  такое, что не для одной системы чисел
такое, что не для одной системы чисел  , где
, где  число
число  не делится на
не делится на 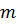 , то уравнение
, то уравнение  не имеет решений в целых числах.
не имеет решений в целых числах.
Например, доказательство того, что для натурального 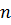 уравнение
уравнение  не имеет решений в целых числах, можно провести посредством проверки, показать, что для
не имеет решений в целых числах, можно провести посредством проверки, показать, что для  и для любого целого
и для любого целого  число
число 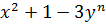 или, что то же самое, число
или, что то же самое, число  не делится на 3 (действительно:
не делится на 3 (действительно: 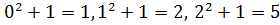 ).
).
Однако не для каждого многочлена с целыми коэффициентами, для которого уравнение  не разрешимо в целых числах
не разрешимо в целых числах  существует натуральное число
существует натуральное число 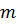 такое, что ни для какой системы целых чисел
такое, что ни для какой системы целых чисел  число
число  не делится на
не делится на 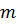 .
.
В самом деле, уравнение  , очевидно, не имеет решений в целых числах
, очевидно, не имеет решений в целых числах  . С другой стороны, если
. С другой стороны, если 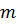 - натуральное число, то как известно,
- натуральное число, то как известно, 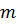 можно представить в виде
можно представить в виде 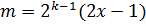 , где
, где  и
и  натуральные числа. Число
натуральные числа. Число  делится на
делится на  , поэтому существует такое натуральное число
, поэтому существует такое натуральное число  , что
, что  Итак, имеем
Итак, имеем  , отсюда видно, что число
, отсюда видно, что число  делится на
делится на 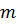 .
.
Анджей Шинцель обнаружил, что для каждого натурального числа 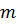 существует целое число
существует целое число 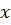 из последовательности
из последовательности  такое, что число
такое, что число  делится на
делится на 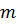 , хотя уравнение
, хотя уравнение  и не имеет ни одного целого корня.
и не имеет ни одного целого корня.
§4. Уравнение вида 
Теорема 4.1. Уравнение
 (4.1)
(4.1)
имеет бесконечное множество решений в натуральных числах  .
.
Доказательство.
Заметим, что (1, 1)-решение уравнения (4.1) и, что если  - его решение, то
- его решение, то  , где
, где  , также есть решение этого уравнения.
, также есть решение этого уравнения.
Действительно,
 .
.
Предположим, что  есть решение уравнения (4.1) в натуральных числах, причем
есть решение уравнения (4.1) в натуральных числах, причем 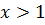 и следовательно, как это вытекает из (4.1)
и следовательно, как это вытекает из (4.1)  .
.
Покажем, что тогда  ,
,  ,
, 
 . (4.5)
. (4.5)
Предположим, что  . Тогда имеем,
. Тогда имеем,  , а также в силу (4.1),
, а также в силу (4.1),  , то получаем
, то получаем  , или,
, или,  что дает
что дает 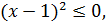 и, следовательно,
и, следовательно,  , а это противоречит предположению
, а это противоречит предположению 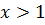 . Итак, первое из равенств доказано.
. Итак, первое из равенств доказано.
Пусть теперь  . Тогда имеем
. Тогда имеем  , а так как, в силу (4.1),
, а так как, в силу (4.1),  , то получаем
, то получаем  , чего быть не может, т.к.
, чего быть не может, т.к. 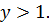 Итак, доказано и второе из неравенств (4.5), из которого уже непосредственно вытекает третье.
Итак, доказано и второе из неравенств (4.5), из которого уже непосредственно вытекает третье.
Положим теперь
 (4.6)
(4.6)
на основании (4.5) заключаем, что  и
и  - натуральные числа, причем
- натуральные числа, причем  и, следовательно,
и, следовательно,  . Рассмотрим выражение
. Рассмотрим выражение

 , если
, если  - решение уравнения (4.1). Поэтому (
- решение уравнения (4.1). Поэтому (  ,
,  )-решение уравнения (4.1).
)-решение уравнения (4.1).
Покажем далее  ,
,
т.е. каждой точке плоскости с координатами  , приведем в соответствие точку той же плоскости с координатами
, приведем в соответствие точку той же плоскости с координатами 
Итак, если  есть решение уравнения (4.1) в натуральных числах
есть решение уравнения (4.1) в натуральных числах  , где
, где 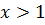 , (
, (  ,
,  )=
)= 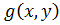 также есть решение уравнения (4.1) в натуральных числах
также есть решение уравнения (4.1) в натуральных числах  ,
,  , где
, где  . Если
. Если  , то подобным же образом, исходя из решения (
, то подобным же образом, исходя из решения (  ,
,  ), получим новое решение (
), получим новое решение (  ,
,  )=
)= 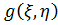 =
=  в натуральных числах
в натуральных числах  ,
,  , где
, где  <
<  и т.д. Вводя обозначение
и т.д. Вводя обозначение  , мы получим таким образом последовательность решений
, мы получим таким образом последовательность решений  ,
,  ,
,  , … уравнения (4.1) во все меньших натуральных числах. Так как последовательность натуральных чисел убывающая, то она не может быть бесконечной и при некотором натуральном
, … уравнения (4.1) во все меньших натуральных числах. Так как последовательность натуральных чисел убывающая, то она не может быть бесконечной и при некотором натуральном 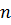 получим решение
получим решение  .
.
Итак, если  - произвольное решение уравнения (3.1) в натуральных числах, где
- произвольное решение уравнения (3.1) в натуральных числах, где 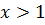 , то существует натуральное число
, то существует натуральное число 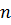 такое, что
такое, что  . (*)
. (*)
Примем  легко проверить, что
легко проверить, что  откуда при помощи индукции легко находим, что (*)
откуда при помощи индукции легко находим, что (*)  .
.
С другой стороны, если примем  , то
, то  будут решением (4.1) если
будут решением (4.1) если  -решение (3.1).
-решение (3.1).
Учитывая полученные выше результаты, заключаем, что все решения (4.1) в натуральных числах  содержаться в бесконечной последовательности
содержаться в бесконечной последовательности  ,
,  , …
, …
4.2. Уравнение  .
.
Теорема 4.2:  не имеет решений в натуральных числах
не имеет решений в натуральных числах  .
.
Доказательство.
Предположим противное. Найдутся натуральные числа  такие, что
такие, что 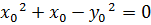 , или
, или 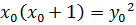 , т.е. квадрат натурального числа равен произведению
, т.е. квадрат натурального числа равен произведению  последовательных чисел
последовательных чисел  и
и  .
.
Как известно для натурального  числа
числа  и
и  являются взаимно простыми (если бы они имели общий делитель
являются взаимно простыми (если бы они имели общий делитель  , то он был бы делителем их разности, т.е. числа 1. что невозможно). Но, как известно из арифметики, если квадратное число есть произведение двух натуральных взаимно простых чисел, то каждый из этих сомножителей должен быть квадратом натурального числа. Поэтому, если бы существовали натуральные числа
, то он был бы делителем их разности, т.е. числа 1. что невозможно). Но, как известно из арифметики, если квадратное число есть произведение двух натуральных взаимно простых чисел, то каждый из этих сомножителей должен быть квадратом натурального числа. Поэтому, если бы существовали натуральные числа  и
и 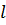 такие, что
такие, что  ,
,  , то отсюда
, то отсюда 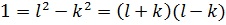 , что для натуральных чисел
, что для натуральных чисел  и
и 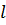 невозможно (т.к. первый сомножитель правой части ≥ 2).
невозможно (т.к. первый сомножитель правой части ≥ 2).
Итак, предположение, что уравнение  имеет решения в натуральных числах
имеет решения в натуральных числах  приводит к противоречию. Следовательно, это уравнение не имеет решений в натуральных числах.
приводит к противоречию. Следовательно, это уравнение не имеет решений в натуральных числах.
Следствие 4.1. Для натуральных  уравнение
уравнение
 (4.3)
(4.3)
не имеет решений в натуральных числах  .
.
На практике удобно использовать следующее утверждение.
Теорема 4.3. Пусть  . Тогда все решения уравнения (4.1) в натуральных числах содержатся в бесконечной последовательности [
. Тогда все решения уравнения (4.1) в натуральных числах содержатся в бесконечной последовательности [ 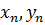 ] для
] для 
{ 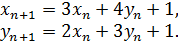
 (4.4)
(4.4)
§5. Уравнение 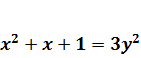 .
.
Теорема 5.1. Дано уравнение  . (5.1)
. (5.1)
Пусть  - решение уравнения (5.1) в натуральных числах содержится в бесконечной последовательности {
- решение уравнения (5.1) в натуральных числах содержится в бесконечной последовательности { 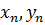 } для
} для 
{ 
 (5.2)
(5.2)
Доказательство аналогично (4.1) [12].
В 1950 г. Р. Облай высказал предположение, что кроме решения  , оно не имеет других решений в натуральных числах
, оно не имеет других решений в натуральных числах  , где
, где 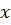 есть нечетное число. В том же году Т. Нагель указал решение
есть нечетное число. В том же году Т. Нагель указал решение  . Метод, аналогичный приведенному выше для уравнения
. Метод, аналогичный приведенному выше для уравнения  , позволит нам определить все решения уравнения (5.1) в натуральных числах
, позволит нам определить все решения уравнения (5.1) в натуральных числах  .
.
Предположим, что  есть решение уравнения (5.1) в натуральных числах, причем
есть решение уравнения (5.1) в натуральных числах, причем 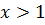 . Можно легко убедиться, что уравнение (5.1) не имеет решений в натуральных числах
. Можно легко убедиться, что уравнение (5.1) не имеет решений в натуральных числах  поэтому должно быть
поэтому должно быть  .
.
Покажем, что  . (5.3)
. (5.3)
Если бы было 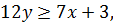 мы имели бы
мы имели бы  , а так как, ввиду (6.1),
, а так как, ввиду (6.1),  , то было бы
, то было бы  , откуда
, откуда  и значит, учитывая, что
и значит, учитывая, что  ,
,  , что невозможно. Итак, первое из неравенств (5.3) доказано.
, что невозможно. Итак, первое из неравенств (5.3) доказано.
Если бы было  , мы имели бы
, мы имели бы  , а так как, ввиду (5.1),
, а так как, ввиду (5.1),  , то было бы
, то было бы  , т.е.
, т.е.  , что невозможно. Таким образом, доказано второе из неравенств (5.3), из которого уже непосредственно вытекает третье.
, что невозможно. Таким образом, доказано второе из неравенств (5.3), из которого уже непосредственно вытекает третье.
Положим теперь
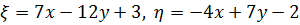 (5.4)
(5.4)
На основании (5.3), найдем, что  ,
, 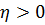 и
и  и, значит,
и, значит,  . Согласно (5.4), имеем
. Согласно (5.4), имеем  , откуда, ввиду (5.1),
, откуда, ввиду (5.1),  .
.
Примем,  .
.
Итак, можно сказать, что исходя из любого решения  уравнения (5.1) в натуральных числах, где
уравнения (5.1) в натуральных числах, где 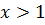 , мы получаем новое решение
, мы получаем новое решение  =
= 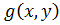 уравнения (5.1) в натуральных числах
уравнения (5.1) в натуральных числах  , где
, где  (и значит, решение в меньших натуральных числах). Отсюда, действуя как выше, найдем, что для каждого решения уравнения (5.1) в натуральных числах
(и значит, решение в меньших натуральных числах). Отсюда, действуя как выше, найдем, что для каждого решения уравнения (5.1) в натуральных числах  , где
, где 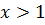 , найдется натуральное число
, найдется натуральное число 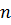 такое, что
такое, что  .
.
Приняв же  , (5.5) легко найдем, что
, (5.5) легко найдем, что  и, следовательно,
и, следовательно,  .
.
С другой стороны, легко проверить, что если  есть решение уравнения (5.1) в натуральных числах, то
есть решение уравнения (5.1) в натуральных числах, то  также есть решение уравнения (5.1) в натуральных числах.
также есть решение уравнения (5.1) в натуральных числах.
Приняв  ,
,  для
для  получим последовательность
получим последовательность  для
для  содержащую все решения уравнения (5.1) в натуральных числах.
содержащую все решения уравнения (5.1) в натуральных числах.
Здесь мы имеем  , следовательно, в силу (5.5), получим
, следовательно, в силу (5.5), получим 
 (5.6) – формулы, позволяющие последовательно определять все решения
(5.6) – формулы, позволяющие последовательно определять все решения  уравнения (5.1) в натуральных числах.
уравнения (5.1) в натуральных числах.
Таким путем легко получаем решения

Этих решений имеется, очевидно, бесконечное множество.
Из равенств  и (5.5) при помощи индукции легко находим, что числа
и (5.5) при помощи индукции легко находим, что числа  с нечетными индексами являются нечетные, с четными – четные, а числа
с нечетными индексами являются нечетные, с четными – четные, а числа  суть нечетные для
суть нечетные для  Для получения всех решений уравнения (5.1) в целых числах
Для получения всех решений уравнения (5.1) в целых числах  , как нетрудно доказать, следовало бы к уже полученным решениям
, как нетрудно доказать, следовало бы к уже полученным решениям  присоединить
присоединить 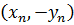 и
и  для
для 
Так что здесь мы пишем, например, еще такие решения:

А. Роткевич заметил, что из всех решений уравнения (5.1) в натуральных числах 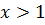 и
и  можно получить все решения уравнения
можно получить все решения уравнения
 (5.7)
(5.7)
в натуральных числах  .
.
В самом деле, допустим, что натуральные числа  . удовлетворяют уравнению (5.7). Положив
. удовлетворяют уравнению (5.7). Положив  , получим, как легко проверить, натуральные числа
, получим, как легко проверить, натуральные числа 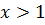 и
и  , удовлетворяющие уравнению (5.1).
, удовлетворяющие уравнению (5.1).
С другой стороны, если натуральные числа 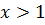 и
и  удовлетворяют уравнению (5.1), то имеем, как легко проверить,
удовлетворяют уравнению (5.1), то имеем, как легко проверить,  , откуда следует, что число (натуральные)
, откуда следует, что число (натуральные)  делится на 3, следовательно,
делится на 3, следовательно,  , где
, где  имеет место равенство
имеет место равенство  , которое доказывает, что числа
, которое доказывает, что числа  удовлетворяют уравнению (5.7).
удовлетворяют уравнению (5.7).
Таким образом, исходя из решений
 уравнения (5.1), получаем решения
уравнения (5.1), получаем решения
 уравнения (5.7).
уравнения (5.7).
Заметим здесь еще, что если натуральные числа  удовлетворяют уравнению (5.7), то указано, что
удовлетворяют уравнению (5.7), то указано, что  есть сумма двух последовательных квадратов, например,
есть сумма двух последовательных квадратов, например, 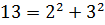 ,
,  .
.
Подобным образом, как раннее для уравнения (5.1) мы могли бы найти все решения уравнения
 (5.8)
(5.8)
в натуральных числах  , приняв для
, приняв для 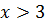

и для 
 ,
,
что приводит к формуле  и к выводу, что все решения уравнения (5.8) в натуральных числах
и к выводу, что все решения уравнения (5.8) в натуральных числах  содержаться в последовательности
содержаться в последовательности  для
для  где
где  ,
,  ,
, 
Например,  ;
;  ;
; 
Геометрический смысл рассмотренного уравнения состоит в том, что оно дает все пифагоровы треугольники (прямоугольные с натуральными сторонами), катеты которых выражаются последовательными натуральными числами. Таких треугольников имеется бесконечно множество.
Уравнение же  , как сказано, не имеет решений в натуральных числах
, как сказано, не имеет решений в натуральных числах  , но
, но  , причем можно доказать, что это единственное решение в натуральных числах уравнения
, причем можно доказать, что это единственное решение в натуральных числах уравнения
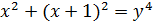 .
.
§6. Уравнение вида  .
.
Рассмотрим вопрос о разрешимости уравнения


