Уравнения второй степени с более двумя неизвестными.

7.1. Примеры уравнений второй степени с тремя неизвестными.

Прежде всего здесь представляет интерес уравнение

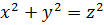. (7.1)

Определение 7.1. Натуральные числа удовлетворяющие уравнению, составляют так называемый пифагоров треугольник.

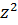Обозначим через α НОД чисел . Тогда , , примем и уравнение (7.1) примет вид . Отсюда следует, что делится на и значит, кратно .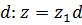

Теперь уравнение (7.1) можно записать в виде

;

сокращая на , получим: .

Мы пришли к уравнению того же вида, что и исходное, причем теперь величины взаимно простые. Таким образом, при решении уравнения (7.1) можно ограничиться случаем, когда . Тогда хотя бы одна из величин (например, ) будет нечетной.

Перенося в правую часть уравнения (7.1), получим:

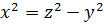; . (7.2)

Обозначим через НОД выражений

Так как 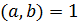, то полученное равенство возможно только в том случае, когда будут полными квадратами (известно, что произведение двух взаимно простых чисел может быть полным квадратом только тогда, когда каждый множитель – полный квадрат):

Но тогда и . (7.4)

Найдем теперь и из равенств (7.3). Сложение этих равенств дает:

. (7.5)

Вычитая второе из равенств (7.3) из первого, получим

;

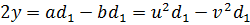. (7.6)

В силу нечетности из (7.1) получаем, что также нечетны. Более того, , так как иначе из равенств (7. 4) и (7.6) следовало бы, что , что противоречит предположению об их взаимной простоте. Числа 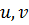связаны со взаимно простыми числами равенствами и в силу этого сами взаимно просты; так как , то , что ясно из равенств (8.3).

Подставляя в равенства (7.4), (7.5) и (7.6) , получаем формулы:

, , , (7.7)

дающие при нечетных взаимно простых ( ) все свободные от общих делителей тройки целых положительных чисел , удовлетворяющие уравнению (7.1).

Для начальных значений формулы (7.7) приводят к следующим часто встречающимся равенствам:

, ( ),

, ( ).

Как уже было сказано, формулы (7.7) дают только те решения уравнения (7.1), в которых числа не имеют общих делителей. Все остальные целые положительные решения этого уравнения получаются домножением решений, содержащихся в формулах (7.7) на произвольный (натуральный) общий множитель .

Тем же путем, каким мы получим все решения уравнения (7.1) в натуральных числах, могут быть получены и все решения других уравнений того же типа.

Найдем все решения уравнения

(7.8)

в натуральных, попарно взаимно простых числах .

Заметим, что если есть решение уравнения (7.8) и не имеют общего делителя, отличного от 1, то они и попарно взаимно просты.

Действительно, если кратны простому числу , то из равенства

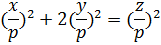
следует, что кратно (так как левая часть – целое число). То же самое будет, если или делятся на .

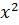Заметим, что должно быть числом нечетным. Действительно, если четно, то левая часть уравнения (7.8) будут четными числами и, значит, также будет четным. Но тогда и 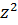будут кратны 4. Отсюда следует, что должны делиться на 4, другими словами, что тоже должны быть четным числом. Чего быть не может, так как попарно взаимно просты.

Если - нечетно, то и должно быть тоже нечетным. Перенося 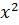в правую часть, мы получаем .

Но и имеют НОД, равный 2ю Действительно, пусть их НОД равен . Тогда , , где целые взаимно простые числа. Складывая и вычитая эти равенства, мы будем иметь: , .

Но и нечетны и взаимно просты. Поэтому НОД 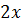и будет 2. Отсюда следует, что .

Итак, или , или нечетно. Поэтому или числа

взаимно просты, или просты числа

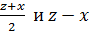В первом случае из равенства следует, что , , 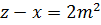а во втором случае из равенства следует, что , , 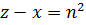где 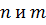- целые, 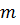- нечетное число, . Решая эти две системы уравнений относительно и и находя y, мы получаем или

или

где 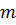- нечетно. Определяя эти две формулы представления решения мы получаем общую формулу:

где 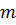–нечетно. Но, для того чтобы были целыми числами, необходимо, чтобы -было четным. Полагая и мы получаем окончательно общие формулы, дающие все решения уравнения (7.8) в целых положительных, без общего делителя, большего 1, числах :

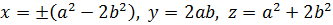, (7.9)

где положительны, взаимно просты и нечетно.

При этих условиях величины выбираются произвольно, но так, чтобы было положительно. Формулы (7.9) действительно дают все решения в целых положительных и взаимно простых числах так как, с одной стороны, мы доказали, что в этом случае должны представляться по формулам (7.9), а с другой стороны, если мы задали числа , удовлетворяющие нашим условиям, то будут действительно взаимно просты и будут решением уравнения (7.8).

Можно найти все решения уравнения

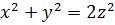(7.10)

в натуральных числах . Это уравнение легко приводиться к уравнению вида (7.1).

В самом деле, если целые числа удовлетворяют уравнению (7.10), то они должны быть одновременно либо оба четными, либо оба нечетные. Поэтому числа

, .

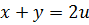Тогда

и, следовательно, .

С другой стороны, если , то приняв , , получим .

Уравнение же 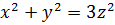не имеет решений в целых числах, отличных от нуля; последнее можно легко проверить, исходя из того факта, что квадрат целого числа, не делящегося на 3, дает при делении на 3 в остатке 1.

Обобщение уравнения (7.1) является уравнение

, (7.11)

где заданное натуральное число. Докажем, что оно имеет бесконечное множество решений в натуральных числах таких, что числа взаимно просты.

В самом деле, если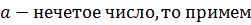

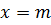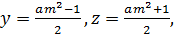
где любое натуральное нечетное число. Тогда

Числа здесь натуральные, причем числа взаимно просты, так как из уравнения (7.11) вытекает, что их общий делитель является делителем числа , следовательно, является также делителем числа .

Если же есть четное число, то приняв

где ппроизвольное натуральное число, получим натуральные числа такие, что , причем числа нечетные. А так как каждый общий делитель чисел является делителем числа , то, как число нечетное, он будет делителем числа 1. Отсюда следует, что числа , а значит, также и числа взаимно просты.

Уравнение имеет бесконечное множество решений в натуральных числах , что вытекает непосредственно из тождества

Действительно,

Например, .

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒