Диофантовы уравнения первого и второго порядка с двумя неизвестными.
Уровень А:
Пример 1. Решить уравнение  в целых числах.
в целых числах.
Решение. Перепишем уравнение в виде 
Число слева делится на 5, следовательно, должно делиться на 5 и число справа. Рассмотрим всевозможные остатки от деления  на 5.
на 5.
1. Если 
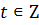 , то
, то  не делится на 5.
не делится на 5.
2. Если 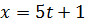 , то
, то 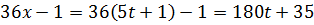 делится на 5.
делится на 5.
В рассмотрении других остатков нет необходимости, так как при других остатках правая часть делиться на 5 не будет. Итак, 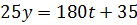 или
или 
Далее будем рассуждать аналогично. Число слева делится на 5, следовательно, делится на 5 и число справа.
1. Если 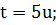
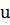
 , то
, то  не делится на 5.
не делится на 5.
2. Если  , то
, то 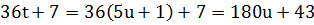 не делится на 5.
не делится на 5.
3. Если  , то
, то  не делится на 5.
не делится на 5.
4. Если  , то
, то  делится на 5.
делится на 5.
В рассмотрении других остатков нет необходимости.
Итак, 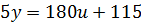 или
или  . Осталось выразить
. Осталось выразить  через
через  .
.
Ответ: {( 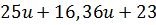 )};
)};  [11].
[11].
Метод рассмотрения остатков становится неэффективным, если числа  и
и  являются большими простыми числами. В этом случае применяется алгоритм, основанный на последовательном уменьшении по модулю коэффициентов при неизвестных.
являются большими простыми числами. В этом случае применяется алгоритм, основанный на последовательном уменьшении по модулю коэффициентов при неизвестных.
1. Выбор наименьшего по модулю коэффициента (пусть  <
<  ).
).
2. Проведение процедуры уменьшения коэффициентов. Это делается с помощью деления с остатком. Пусть  , где
, где  , тогда
, тогда  .
.
Левая часть последнего уравнения делится на 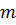 . Значит, должна делиться на
. Значит, должна делиться на 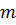 и правая часть:
и правая часть: 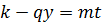 , где
, где 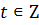 ,
, 
3. Повторение процедуры уменьшения коэффициентов. Новое уравнение отличается от старого только тем, что его коэффициенты по модулю меньше коэффициентов старого. За конечное число шагов добьемся того, что коэффициент при одном из новых неизвестных будет равен 1.
4. Возврат от новых переменных к исходным.
Пример 2. Решить уравнение  в целых числах.
в целых числах.
Решение. Проведем деление с остатком: 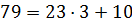 и перепишем исходное уравнение в виде
и перепишем исходное уравнение в виде

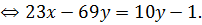
Левая часть последнего уравнения делится нацело на 23, поэтому должна делиться на 23 и правая часть:  или
или  новое неизвестное.
новое неизвестное.
Полученное новое уравнение по типу точно такое же, как исходное. Однако коэффициенты при неизвестных в нем уменьшились по модулю. Повторим процедуру уменьшения коэффициентов еще раз:  Проведем процедуру уменьшения коэффициентов в последний раз:
Проведем процедуру уменьшения коэффициентов в последний раз: 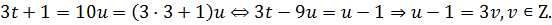
Осталось выразить  через
через  . Поскольку
. Поскольку  , то
, то
1. 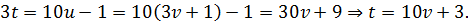
2. 
3. 

Уровень В:
Диофантовы уравнения первого порядка возникают и в некоторых прикладных задачах. Рассмотрим следующее примеры.
Пример 3. Найти все целые  при которых дробь
при которых дробь 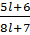 сократима.
сократима.
Решение. Пусть  - общий делитель числителя и знаменателя. Тогда
- общий делитель числителя и знаменателя. Тогда

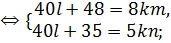
Вычтем из первого равенства второе и получим  откуда
откуда  . Для нахождения
. Для нахождения 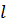 решим в целых числах уравнение
решим в целых числах уравнение  Напомним, что это уравнение можно решить двумя способами: перебором всевозможных остатков и процедурой уменьшения коэффициентов. Решив уравнение, получим
Напомним, что это уравнение можно решить двумя способами: перебором всевозможных остатков и процедурой уменьшения коэффициентов. Решив уравнение, получим 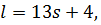 где
где  .
.
Ответ: 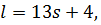
 .
.
Уровень С:
Пример 4. Решить уравнение 
Решение. Преобразуем данное уравнение следующим образом:
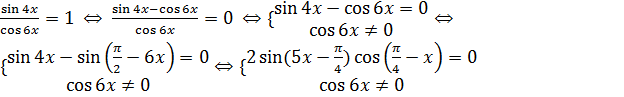

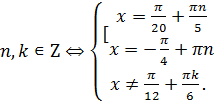
Решим два уравнения в целых числах. Рассмотрим сначала первое уравнение:

Перебирая все возможные остатки при делении  на 5, находим, что решением последнего уравнения является
на 5, находим, что решением последнего уравнения является 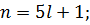
 . Значит решением задачи будут служить
. Значит решением задачи будут служить  , где
, где  ,
,  ;
;  . Теперь рассмотрим второе уравнение:
. Теперь рассмотрим второе уравнение: 
Ясно, что любое целое  является решением этого уравнения. Таким образом, ни одно значение
является решением этого уравнения. Таким образом, ни одно значение  из серии
из серии  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Ответ:  ;
;  ;
;  .
.
Пример 5. Целое число кратно 7 и при делении на 4 дает в остатке 3. Найти остаток от деления этого числа на 28.
Решение. Пусть  Имеем
Имеем

Перебирая все возможные остатки при делении  на 4, находим, что решение последнего уравнения
на 4, находим, что решение последнего уравнения  .
.
Таким образом,  и дает остаток 7 при делении на 28.
и дает остаток 7 при делении на 28.
Ответ: 7.
Диофантовым уравнением второго порядка с двумя неизвестными  будем называть уравнение вида
будем называть уравнение вида  , где А, В, С, D, Е, F, х, у ∊ Z и хотя бы одно из чисел А, В, С отлично от нуля. Общая теория решения таких уравнений достаточно сложна, поэтому приведем лишь основные методы.
, где А, В, С, D, Е, F, х, у ∊ Z и хотя бы одно из чисел А, В, С отлично от нуля. Общая теория решения таких уравнений достаточно сложна, поэтому приведем лишь основные методы.
Одним из таких методов является разложение на множители. Он состоит в том, что левая часть данного уравнения каким-либо образом раскладывается на множители (чаще всего путем нахождения дискриминанта), и задача сводится к перебору конечного числа вариантов.
Уровень А:
Пример 6. Найти все пары целых чисел  , каждая из которых удовлетворяет уравнению
, каждая из которых удовлетворяет уравнению 
Решение. Преобразуем данное уравнение следующим образом:

⇔ 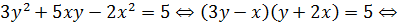

Первые две системы не имеют решений в целых числах, третья и четвертая имеют решением пары 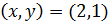 и
и  соответственно.
соответственно.
Ответ: {  }
}
Пример 7. Найти все пары натуральных чисел разной четности, удовлетворяющие уравнению  .
.
Решение. Преобразуем данное уравнение следующим образом:


Так как  — натуральные числа разной четности, возможны следующие варианты:
— натуральные числа разной четности, возможны следующие варианты:

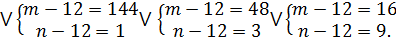
Здесь учитываем, что числа  и
и  будут также разной четности, кроме того, оба этих числа должны быть положительны, иначе
будут также разной четности, кроме того, оба этих числа должны быть положительны, иначе 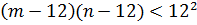 . Таким образом, решением задачи будут служить пары
. Таким образом, решением задачи будут служить пары 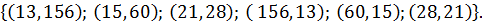
Ответ: 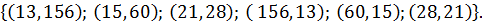
Пример 8. Найти все тройки чисел  , удовлетворяющие системе уравнений
, удовлетворяющие системе уравнений

Рассмотрим второе уравнение системы как квадратное относительно  . Это уравнение будет иметь решение тогда и только тогда, когда его дискриминант больше или равен нулю. Имеем:
. Это уравнение будет иметь решение тогда и только тогда, когда его дискриминант больше или равен нулю. Имеем:

В первом случае 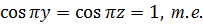
 при этом
при этом  Первое уравнение системы в этом случае имеет вид
Первое уравнение системы в этом случае имеет вид

и не будет иметь решений, так как в левой части этого уравнения всегда будет получаться четное число.
Во втором случае  откуда следует, что
откуда следует, что 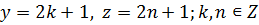 , при этом
, при этом  Первое уравнение системы в этом случаем преобразуется к виду
Первое уравнение системы в этом случаем преобразуется к виду  .
.
Дискриминант этого уравнения (которое мы рассматриваем относительно  ) равен
) равен  , иначе число
, иначе число  не может быть целым. Последнее уравнение принимает вид:
не может быть целым. Последнее уравнение принимает вид:  .
.
Разность первого и второго чисел, стоящих в скобках, равна 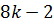 , т.е. дает остаток 6 при делении на 8. В соответствии с этим получается четыре варианта:
, т.е. дает остаток 6 при делении на 8. В соответствии с этим получается четыре варианта:

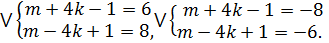
В первых двух случаях получаем 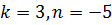 , откуда
, откуда  , в третьем и четвертом случаях находим, что
, в третьем и четвертом случаях находим, что  и
и 
Ответ: 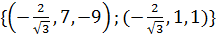 .
.
Уровень В:
Если в уравнении отсутствует член, содержащий 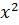 или
или  , т.е.
, т.е.  или
или  равны нулю, но при этом
равны нулю, но при этом  , то такое уравнение решается методом выделения целой части. Пусть, например,
, то такое уравнение решается методом выделения целой части. Пусть, например,  . Выразим
. Выразим  через
через  :
:

откуда  Далее делим многочлен
Далее делим многочлен 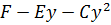 на многочлен
на многочлен  с остатком, т.е. представляем данную дробь в виде
с остатком, т.е. представляем данную дробь в виде
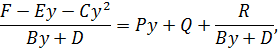
где 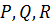 -рациональные числа. Подобрав, при необходимости, целое
-рациональные числа. Подобрав, при необходимости, целое 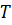 и домножив на него обе части уравнения
и домножив на него обе части уравнения  получим уравнение
получим уравнение

где  уже являются целыми числами. Дальнейшее решение сводится к перебору всех делителей числа
уже являются целыми числами. Дальнейшее решение сводится к перебору всех делителей числа  (если
(если  ).
).
Пример 9. Решить в целых числах уравнение 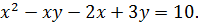
Решение. Выразим в данном уравнении  через
через  :
:

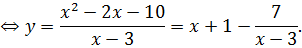
Из полученного равенства видно, что дробь 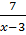 должна быть целым числом. Это возможно, когда
должна быть целым числом. Это возможно, когда  принимает значения
принимает значения  и
и  . Разбирая четыре случая, находим все пары
. Разбирая четыре случая, находим все пары  , удовлетворяющих данному уравнению:
, удовлетворяющих данному уравнению: 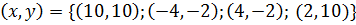 .
.
Ответ:  .
.
Пример 10. Найти все корни уравнения  являющиеся целыми числами.
являющиеся целыми числами.
Решение. Преобразуем данное уравнение следующим образом:




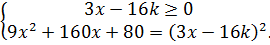
Рассмотри второе уравнение системы:







При этом равенство  получается путем деления в столбик многочлена
получается путем деления в столбик многочлена  на многочлен
на многочлен  .
.
Далее, так как числа  и
и  - целые, также целым должно быть число
- целые, также целым должно быть число  , т.е.
, т.е.  . Поскольку
. Поскольку  , имеем
, имеем  или
или  . Если
. Если  , то
, то 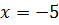 , что не удовлетворяет условию
, что не удовлетворяет условию 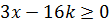 . Если
. Если  , то
, то  , что удовлетворяет условию
, что удовлетворяет условию 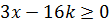 . Если
. Если  , то
, то  , что удовлетворяет условию
, что удовлетворяет условию 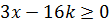 . Следовательно, решением задачи будут служить
. Следовательно, решением задачи будут служить  и
и  .
.
Ответ:  ,
,  .
.
Пример 11. Какие из значений: 8, 43, 2010 может принимать  , если известно, что уравнение
, если известно, что уравнение 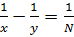 имеет единственное решение в натуральных числах
имеет единственное решение в натуральных числах  ?
?
Решение. Пусть  некоторое натуральное число. Считая
некоторое натуральное число. Считая  натуральными числами, преобразуем данное уравнение следующим образом:
натуральными числами, преобразуем данное уравнение следующим образом:


Из полученного равенства следует, что число  должно быть целым. Если
должно быть целым. Если  — простое число, то число
— простое число, то число  имеет единственный делитель, больший
имеет единственный делитель, больший  (равный
(равный  ). Поэтому данное уравнение имеет в натуральных числах единственное решение:
). Поэтому данное уравнение имеет в натуральных числах единственное решение:  . Если же N - составное, существуют, по крайней мере, два числа, большие N и являющиеся делителями
. Если же N - составное, существуют, по крайней мере, два числа, большие N и являющиеся делителями  . Например, если
. Например, если  , где
, где  - натуральные числа такие, что
- натуральные числа такие, что  , то
, то  и
и 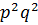 больше
больше  и являются делителями
и являются делителями  . Значит, в этом случае данное уравнение будет иметь, по крайней мере, два различных решения. Таким образом, из трех предложенных чисел только
. Значит, в этом случае данное уравнение будет иметь, по крайней мере, два различных решения. Таким образом, из трех предложенных чисел только  удовлетворяет условию задачи.
удовлетворяет условию задачи.
Ответ:  .
.
Уровень С:
Пример 12. Решить уравнение
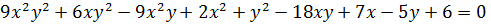 в целых числах.
в целых числах.
Решение. Рассмотрим данное уравнение как квадратное относительно  . Имеем
. Имеем 
Дискриминант этого уравнения равен 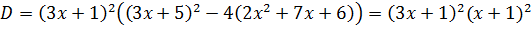 .
.
Так как при всех целых значениях переменной  число
число  отлично от нуля, корни квадратного уравнения равны
отлично от нуля, корни квадратного уравнения равны
 .
.
В первом случае получаем уравнение
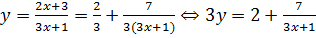 .
.
Перебирая для числа  все возможные делители числа 7, находим, что решением этого уравнения являются пары
все возможные делители числа 7, находим, что решением этого уравнения являются пары  Во втором случае уравнение принимает вид
Во втором случае уравнение принимает вид
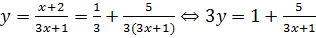 .
.
Здесь 5 делится нацело на  , и решением этого уравнения будут служить пары чисел
, и решением этого уравнения будут служить пары чисел 
Таким образом, ответ к задаче будет состоять из четырех пар чисел 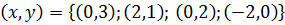 .
.
Ответ:  .
.
Если диофантово уравнение второго порядка каким-либо образом (например, выделением полных квадратов) приводится к виду 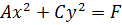 , где
, где  целые, отличные от нуля, числа, то метод решения зависит от знаков коэффициентов при переменных. Если
целые, отличные от нуля, числа, то метод решения зависит от знаков коэффициентов при переменных. Если  имеют один и тот же знак, то используются следующие оценки (пусть
имеют один и тот же знак, то используются следующие оценки (пусть  ):
):
 .
.
Далее задача сводится к перебору конечного числа вариантов. Если же 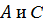 имеют разные знаки, то в общем виде решение уравнения достаточно сложно, но в некоторых случаях можно, например, перебором остатков доказать, что уравнение не имеет решений в целых числах.
имеют разные знаки, то в общем виде решение уравнения достаточно сложно, но в некоторых случаях можно, например, перебором остатков доказать, что уравнение не имеет решений в целых числах.
Пример 13. Найти целочисленные решения уравнения

Решение. Рассмотрим данное уравнение как квадратное относительно 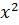 .
.
Имеем: 
Дискриминант этого уравнения равен 
Корни уравнения равны

или
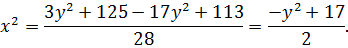
Таким образом, левая часть исходного уравнения раскладывается на множители следующим образом:

и задача сводится к решению двух уравнений в целых числах.
Докажем сначала, что уравнение  не имеет целочисленных решений. Для этого посмотрим, какие остатки могут давать при делении на 3 левая и правая части этого уравнения. Так как любой полный квадрат дает при делении на 3 остаток 0 или остаток 1, число
не имеет целочисленных решений. Для этого посмотрим, какие остатки могут давать при делении на 3 левая и правая части этого уравнения. Так как любой полный квадрат дает при делении на 3 остаток 0 или остаток 1, число  также дает при делении на 3 остатки 0 и 1. Остатки от деления на 3 числа
также дает при делении на 3 остатки 0 и 1. Остатки от деления на 3 числа  могут быть равны 0 или 2. Таким образом, равенство может иметь место только в том случае, когда
могут быть равны 0 или 2. Таким образом, равенство может иметь место только в том случае, когда  и
и  кратны 3. Но в этом случае числа
кратны 3. Но в этом случае числа 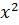 и
и  делятся без остатка на 9, поэтому равенство также не может иметь место (поскольку 3 не делится на 9).
делятся без остатка на 9, поэтому равенство также не может иметь место (поскольку 3 не делится на 9).
Рассмотрим теперь уравнение 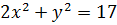 . Из оценки
. Из оценки  8, 5 сразу следует, что
8, 5 сразу следует, что  по модулю не превосходит 2. Перебирая все возможные варианты, находим, что решением задачи будут служить пары чисел
по модулю не превосходит 2. Перебирая все возможные варианты, находим, что решением задачи будут служить пары чисел
(  ,
, 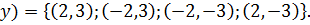
Ответ: 
Наконец, рассмотрим уравнение вида  де
де  -целые числа и
-целые числа и  , и
, и  отличны от нуля. Это уравнение решается перебором остатков при делении на
отличны от нуля. Это уравнение решается перебором остатков при делении на  числа
числа  Но в отличие от уравнений первого порядка разрешимость данного уравнения может быть и при нескольких значениях остатка
Но в отличие от уравнений первого порядка разрешимость данного уравнения может быть и при нескольких значениях остатка  . Кроме того, может оказаться, что такое уравнение и вовсе не имеет решений.
. Кроме того, может оказаться, что такое уравнение и вовсе не имеет решений.
Пример 14. Решить в целых числах уравнение 
Решение. Перепишем исходное уравнение в виде 
Левая часть полученного уравнения делится на 3, значит, должна делиться на 3 и его правая часть. Рассмотрим три случая.
1. Если 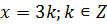 , то
, то 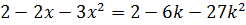 не делится на 3.
не делится на 3.
2. Если 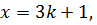 то
то 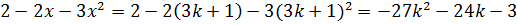 делится на 3.
делится на 3.
3. Если  то
то  не делится на 3.
не делится на 3.
Итак,  , откуда
, откуда  где
где 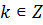 .
.
Ответ: {(  )};
)}; 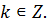
Задачи для самостоятельного решения:
Уровень А:
1. Решить уравнение 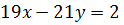 в целых числах.
в целых числах.
2. Найти все целые неотрицательные  , удовлетворяющие уравнению
, удовлетворяющие уравнению 
3. Найти все пары целых чисел (  ,
,  , удовлетворяющих уравнению
, удовлетворяющих уравнению 
4. Найти все целые числа  для которых выполнены условия:
для которых выполнены условия:  и
и 
Уровень В:
5. Найти наименьшее натуральное число  такое, что остаток от деления
такое, что остаток от деления  на 8 на 5 больше остатка от деления
на 8 на 5 больше остатка от деления  на 5 и в 2 раза больше остатка от деления
на 5 и в 2 раза больше остатка от деления  на 7.
на 7.
6. Найти все пары целых неотрицательных чисел  , которые являются решениями уравнения
, которые являются решениями уравнения 
7. Решить в натуральных числах уравнение  , где -заданное простое число.
, где -заданное простое число.
8. Найти все корни уравнения  являющиеся целыми числами.
являющиеся целыми числами.
Уровень С:
9. Найти остаток от деления целого числа  на 30, если известно, что остаток от его деления на 15 равен 4, а остаток от деления на 18 равен
на 30, если известно, что остаток от его деления на 15 равен 4, а остаток от деления на 18 равен
10. На какую минимальную величину могут отличаться друг от друга натуральные числа  , если известно, что дробь
, если известно, что дробь  является натуральным числом? 20. Решить уравнение
является натуральным числом? 20. Решить уравнение 
11. Решить уравнение  .
.
12. Найти все тройки чисел (  ,
,  , удовлетворяющие системе уравнений
, удовлетворяющие системе уравнений 
13. Решить уравнение  в целых числах.
в целых числах.
Популярное:
- I, Верхние передачи мяча двумя руками — 15 мин,
- II. Обучение верхней передаче двумя руками—40 мин.
- Абсолютная монархия в России (признаки, особенности, идеалогия, условия возникновения, реформы Петра первого)
- Административные правонарушения в области охраны историко-культурного наследия. Правонарушения против порядка использования топливно-энергетических ресурсов (Гл. 19,20)
- Апреля 1961 года в 9.07 по московскому времени состоялся старт первого в мире пилотируемого космического корабля, возвестившего всему миру о начале новой космической эры человечества.
- Архитектура 16-разрядного процессора первого поколения
- Архитектура процессоров второго поколения
- Белки является способность образовывать более высокого порядка структуры, такие как разветвленные сети.
- Билет 1 Определители второго порядка и их свойства
- Бросок первого мяча соперника
- В задачах (258–266) вычислить, сколько молей веществ, подчеркнутых в уравнениях реакций, прореагировало или образовалось в результате химических превращений, если при этом выделилось 2500 кДж тепла
- В задачах 392–420 определить электродвижущую силу элементов, написать уравнения реакций, за счет которых возникает разность потенциалов. Составить схемы элементов

