Задачи математических олимпиад.
В данном параграфе рассматриваются задачи на целые числа, предлагавшиеся в разные годы на олимпиадах «Ломоносов» и «Покори Воробьевы горы» по математике, а также Московской математической олимпиаде.
Пример 1. На клетчатой бумаге отмечен прямоугольник 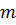 и
и  клеток, причём числа
клеток, причём числа 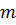 и
и  взаимно просты и
взаимно просты и 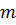 <
<  . Диагональ этого прямоугольника не пересекает ровно 116 его клеток. Найти все возможные значения
. Диагональ этого прямоугольника не пересекает ровно 116 его клеток. Найти все возможные значения 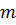 и
и  при данных условиях.
при данных условиях.
Решение. Диагональ прямоугольника не может проходить через узлы клеток, лежащие внутри прямоугольника. Действительно, если бы это было не так, то существовал бы прямоугольник меньшего размера  клеток, причём
клеток, причём  и
и  (
(  - натуральные числа). Тогда числа
- натуральные числа). Тогда числа 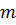 и
и  не являлись бы взаимно простыми, что противоречит условию задачи.
не являлись бы взаимно простыми, что противоречит условию задачи.
Далее, диагональ прямоугольника, пересекая каждую новую клетку, пересекает либо вертикальную, либо горизонтальную линию клетчатой бумаги, находящуюся внутри этого прямоугольника. Это значит, что число пересекаемых ею клеток, уменьшенное на единицу (не рассматривается клетка, прилегающая к той вершине прямоугольника, из которой выходит данная диагональ), равно суммарному количеству вертикальных и горизонтальных линий, лежащих внутри прямоугольника, т.е.  . Итак, число пересекаемых клеток равно
. Итак, число пересекаемых клеток равно  , и из условия задачи получаем уравнение
, и из условия задачи получаем уравнение  .
.
Поскольку 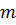 <
<  , пара
, пара  равна либо
равна либо  , либо
, либо  либо
либо  . Первые две пары приводят к ответу, в последнем случае получаются числа
. Первые две пары приводят к ответу, в последнем случае получаются числа  и
и  , не являющиеся взаимно простыми.
, не являющиеся взаимно простыми.
Ответ: 
Пример 2. Каким может быть наибольший общий делитель натуральных чисел 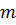 и
и  , если при увеличении числа
, если при увеличении числа 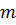 на 6 он увеличивается в 9 раз?
на 6 он увеличивается в 9 раз?
Решение. Пусть  - наибольший общий делитель чисел
- наибольший общий делитель чисел 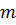 и
и  , тогда
, тогда  -наибольший общий делитель чисел
-наибольший общий делитель чисел  и
и  . Так как
. Так как  - делитель
- делитель 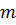 и
и 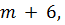 то
то  - делитель разности этих чисел, т.е. делитель числа 6. Следовательно,
- делитель разности этих чисел, т.е. делитель числа 6. Следовательно,  ,
,  или
или  . Так как числа
. Так как числа  и
и  делятся на 9, то числа
делятся на 9, то числа 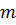 и
и  делятся на 3, следовательно,
делятся на 3, следовательно,  делится на 3. Таким образом,
делится на 3. Таким образом,  или
или  . Осталось проверить, что оба случая имеют место. Если
. Осталось проверить, что оба случая имеют место. Если  , то, например,
, то, например,  ,
,  ; если
; если  , то
, то 
Ответ: 3 или 6.
Пример 3. Каким может быть произведение нескольких различных простых чисел, если оно кратно каждому из них, уменьшенному на 1? Найти все возможные значения этого произведения.
Решение. Пусть  - произведение нескольких различных простых чисел
- произведение нескольких различных простых чисел  удовлетворяющих условию задачи. Поскольку по условию
удовлетворяющих условию задачи. Поскольку по условию  кратно чётному числу
кратно чётному числу  , оно само чётно и
, оно само чётно и  . Число
. Число 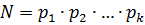 имеет единственный делитель
имеет единственный делитель  , из интервала
, из интервала  но
но  также принадлежит этому интервалу, значит,
также принадлежит этому интервалу, значит,  . Таким образом,
. Таким образом,  , а
, а  может принимать значение
может принимать значение 
Если  , то по условию задачи
, то по условию задачи  , принадлежащее интервалу
, принадлежащее интервалу  , является делителем числа
, является делителем числа  . Этому интервалу может принадлежать единственный делитель
. Этому интервалу может принадлежать единственный делитель  - число
- число  . Следовательно,
. Следовательно,  . Число
. Число 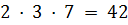 удовлетворяет условию задачи.
удовлетворяет условию задачи.
Если  , то по условию чётное число
, то по условию чётное число  , принадлежащее интервалу
, принадлежащее интервалу  , также является делителем
, также является делителем  . Из чётных делителей числа
. Из чётных делителей числа  этому интервалу могут принадлежать лишь числа
этому интервалу могут принадлежать лишь числа 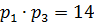 и
и  Число
Число 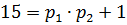 является составным, значит,
является составным, значит, 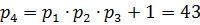 . Число
. Число  удовлетворяет условию задачи.
удовлетворяет условию задачи.
Если  , то по условию чётное число
, то по условию чётное число  , принадлежащее интервалу
, принадлежащее интервалу  , также должно являться делителем
, также должно являться делителем  . Из чётных делителей числа
. Из чётных делителей числа  этому интервалу могут принадлежать лишь числа
этому интервалу могут принадлежать лишь числа  ,
,  и
и 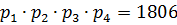 . Каждое из чисел
. Каждое из чисел  является составным. Значит,
является составным. Значит,  числа
числа  не может быть более четырёх различных простых делителей. Таким образом, ответом к задаче будут служить числа
не может быть более четырёх различных простых делителей. Таким образом, ответом к задаче будут служить числа 
Ответ: 
Пример 4. Найти наименьшее натуральное  , для которого число
, для которого число  не является делителем числа
не является делителем числа  где
где 
Решение. Если  , то
, то  будет делиться на
будет делиться на  (так как числа
(так как числа  и
и  содержатся среди чисел
содержатся среди чисел  ). Поскольку верны неравенства
). Поскольку верны неравенства  , то достаточно проверить делимость 2008! на
, то достаточно проверить делимость 2008! на  при
при  .
.
1.  делится на
делится на 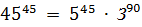 , так как среди чисел
, так как среди чисел  заведомо найдется 45 чисел, кратных 5, и 90 чисел, кратных 3.
заведомо найдется 45 чисел, кратных 5, и 90 чисел, кратных 3.
2. 2008! делится на  , так как среди чисел
, так как среди чисел  заведомо найдется 46 чисел, кратных 2, и 46 чисел, кратных 23, поскольку
заведомо найдется 46 чисел, кратных 2, и 46 чисел, кратных 23, поскольку 
3. 2008! не делится на  , так как число 47 простое, и поэтому среди чисел
, так как число 47 простое, и поэтому среди чисел  есть лишь 42 числа, кратных 47. Действительно,
есть лишь 42 числа, кратных 47. Действительно, 
Замечание. Легко заметить, что для произвольного натурального  наименьшим натуральным
наименьшим натуральным  , для которого
, для которого  не делится на
не делится на  , является наименьшее простое число
, является наименьшее простое число  , большее
, большее  .
.
Ответ: 47.
Пример 5. Для каждого простого  найти наибольшую натуральную степень числа
найти наибольшую натуральную степень числа  , на которую делится число
, на которую делится число  .
.
Решение. Если  кратно (
кратно (  ,
,  , то
, то 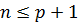 , так как
, так как  входит в разложение числа
входит в разложение числа  на простые множители в степени 1 (а значит, в разложение числа (
на простые множители в степени 1 (а значит, в разложение числа (  - в степени
- в степени  ), а в разложение числа
), а в разложение числа  - в степени
- в степени  . Докажем, что
. Докажем, что  делится на
делится на  .
.
Запишем  различных элементов в виде таблицы
различных элементов в виде таблицы  . Две такие таблицы назовем эквивалентными, если одна получается из другой некоторыми перестановками элементов внутри строк, а также некоторой перестановкой самих строк. Скажем, что все таблицы, эквивалентные данной, образуют класс эквивалентности. Так как
. Две такие таблицы назовем эквивалентными, если одна получается из другой некоторыми перестановками элементов внутри строк, а также некоторой перестановкой самих строк. Скажем, что все таблицы, эквивалентные данной, образуют класс эквивалентности. Так как 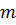 объектов можно переставить
объектов можно переставить 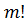 способами, то всего таблиц
способами, то всего таблиц  , количество перестановок в каждой строке -
, количество перестановок в каждой строке -  , количество таблиц, которые можно получить, переставляя элементы внутри строк, -
, количество таблиц, которые можно получить, переставляя элементы внутри строк, -  , количество таблиц в одном классе эквивалентности -
, количество таблиц в одном классе эквивалентности -  . Так как общее число таблиц есть произведение количества таблиц в одном классе эквивалентности на число таких классов, то
. Так как общее число таблиц есть произведение количества таблиц в одном классе эквивалентности на число таких классов, то  , делится на
, делится на  .
.
Ответ: 
Пример 6. Доказать, что для любого натурального числа  существует делящееся на него натуральное число
существует делящееся на него натуральное число  , в десятичной записи которого можно вычеркнуть некоторую ненулевую цифру так, что получившееся число тоже будет делиться на
, в десятичной записи которого можно вычеркнуть некоторую ненулевую цифру так, что получившееся число тоже будет делиться на  .
.
Решение. Рассмотрим для произвольного натурального  число
число  . Пусть
. Пусть 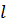 - количество знаков в десятичной записи числа
- количество знаков в десятичной записи числа 
 Заметим, что при достаточно больших
Заметим, что при достаточно больших  (а именно, при
(а именно, при  ) десятичная запись числа
) десятичная запись числа  выглядит следующим образом: сначала идёт десятичная запись числа
выглядит следующим образом: сначала идёт десятичная запись числа  , затем - серия девяток, и наконец - десятичная запись числа
, затем - серия девяток, и наконец - десятичная запись числа  . Таким образом, при
. Таким образом, при  число
число  можно получить из числа
можно получить из числа  путем вычеркивания одной из девяток в центральной части десятичной записи. Очевидно также, что все числа
путем вычеркивания одной из девяток в центральной части десятичной записи. Очевидно также, что все числа  делятся на
делятся на 
Пример 7. Дана последовательность  . Существуют ли пять идущих подряд её членов, делящихся на 2005?
. Существуют ли пять идущих подряд её членов, делящихся на 2005?
Решение. Докажем, что при  , член последовательности с номером
, член последовательности с номером  не делится на 5. Действительно,
не делится на 5. Действительно,  . Числа
. Числа 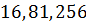 являются числами вида
являются числами вида  . Остаток при делении чисел вида
. Остаток при делении чисел вида  на 5 равен 1, что несложно получить, раскрыв, например, скобки в выражении
на 5 равен 1, что несложно получить, раскрыв, например, скобки в выражении  . Число
. Число  делится, очевидно, на 5 без остатка. Следовательно, число
делится, очевидно, на 5 без остатка. Следовательно, число  дает при делении на 5 остаток 4, т.е. не делится на 5 нацело. Таким образом, не существуют пять идущих подряд членов последовательности
дает при делении на 5 остаток 4, т.е. не делится на 5 нацело. Таким образом, не существуют пять идущих подряд членов последовательности  делящихся на 2005.
делящихся на 2005.
Замечание. Согласно малой теореме Ферма  делится на
делится на  для любого простого числа
для любого простого числа  и любого натурального числа
и любого натурального числа  , не кратного
, не кратного  . При
. При  и
и 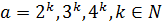 получаем, что
получаем, что  делится на 5, т.е.
делится на 5, т.е.  даёт остаток 1 при делении на 5.
даёт остаток 1 при делении на 5.
Ответ: Нет.
Пример 8. Натуральные числа  таковы, что
таковы, что  и
и  . Найти
. Найти 
Решение. Разложим числа 60 и 270 на простые множители. Имеем:

Пусть теперь

где  - целые неотрицательные числа;
- целые неотрицательные числа;  . Выполнение условий
. Выполнение условий  и
и  означает, что
означает, что  и
и 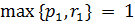 . Следовательно,
. Следовательно, 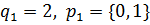 и
и  причём
причём  и
и  , одновременно не равны нулю. Во всех этих случаях
, одновременно не равны нулю. Во всех этих случаях 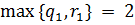
Аналогично  и
и 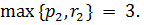 Значит,
Значит,  и
и  и
и  , причём
, причём  и
и 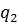 одновременно не равны нулю. Отсюда следует, что
одновременно не равны нулю. Отсюда следует, что  . И, наконец,
. И, наконец, 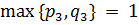 и
и  . Здесь существуют две возможности:
. Здесь существуют две возможности:  или
или  (например, если
(например, если  ,
,  ). Таким образом,
). Таким образом,

Ответ: 
Пример 9. Числа 54 и 128 являются членами геометрической прогрессии. Найти все натуральные числа, которые могут встретиться в этой прогрессии.
Решение. Пусть  , и
, и  - первый член и знаменатель данной геометрической прогрессии,
- первый член и знаменатель данной геометрической прогрессии,  - натуральное число, являющееся
- натуральное число, являющееся  -м членом этой прогрессии. Согласно условию задачи существуют такие натуральные числа
-м членом этой прогрессии. Согласно условию задачи существуют такие натуральные числа 
 , что имеет место следующая система уравнений:
, что имеет место следующая система уравнений:
 ⇒
⇒  ⇒
⇒ 
Так как  , а
, а  , последнее уравнение преобразуется к следующему виду:
, последнее уравнение преобразуется к следующему виду:

Отсюда следует, что, во-первых, существуют такие целые неотрицательные числа  , что
, что  , и, во-вторых, выполняется следующее соотношение:
, и, во-вторых, выполняется следующее соотношение:


Умножим второе уравнение полученной системы на 2 и сложим его с первым уравнением. Имеем:
 (так как
(так как  ).
).
Полученное уравнение имеет четыре пары решений в целых неотрицательных числах: 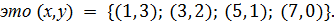 Этим решениям будут соответствовать значения
Этим решениям будут соответствовать значения  , равные 54, 72, 96 и 128. Таким образом, только эти четыре натуральных числа могут встретиться в данной геометрической прогрессии.
, равные 54, 72, 96 и 128. Таким образом, только эти четыре натуральных числа могут встретиться в данной геометрической прогрессии.
Ответ: 54, 72, 96, 128.
Задачи для самостоятельного решения.
1. На клетчатой бумаге отмечен прямоугольник 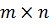 клеток, причём числа
клеток, причём числа  взаимно просты и
взаимно просты и  . Диагональ этого прямоугольника не пересекает ровно 124 его клетки. Найти все возможные значения
. Диагональ этого прямоугольника не пересекает ровно 124 его клетки. Найти все возможные значения  при данных условиях.
при данных условиях.
2. Натуральные числа  таковы, что
таковы, что  и
и  . Найти
. Найти 
3. Числа 24 и 2187 являются членами геометрической прогрессии. Найти все натуральные числа, которые могут встретиться в этой прогрессии.
4. В течение четверти учитель ставил Мише оценки «1», «2», «3», «4» и «5», при этом среднее арифметическое всех его оценок оказалось равным в точности 3, 5. Тогда учитель заменил одну оценку «4» парой оценок «3» и «5». Доказать, что от этого средняя оценка Миши увеличилась. Найти наибольшее возможное ее значение после такой замены: 1) одной оценки «4»; 2) всех его оценок «4».
5. Решить в натуральных числах уравнение 
6. Дана геометрическая прогрессия. Известно, что ее первый, десятый и тридцатый члены - натуральные числа. Верно ли, что её двадцатый член - натуральное число?
7. Решить в целых числах уравнение 
8. В каждом подъезде нового дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. На восьмом этаже третьего подъезда первая квартира имеет номер 106. Какой номер имеет вторая квартира на третьем этаже шестого подъезда?
9. Существует ли такой прямоугольный треугольник, что увеличенные на 1 оба его катета и гипотенуза является, соответственно, катетами и гипотенузой другого прямоугольного треугольника? Тот же вопрос, если все три стороны исходного треугольника не увеличивать, а изменять на 1, т.е. увеличивать или уменьшать - каждую по своему усмотрению.
10. Существует ли 2005 различных натуральных чисел таких, что сумма любых 2004 из них делится на оставшееся число?
11. Найти все возрастающие конечные арифметические прогрессии, которые состоят из простых чисел и у которых количество членов больше, чем разность прогрессии.
12. Петр родился в XIX веке, а его брат Павел - в XX веке. Однажды братья встретились на праздновании своего общего дня рождения. Петр сказал: «Мой возраст равен сумме цифр года моего рождения*. «Мой тоже*, — ответил Павел. На сколько лет Павел младше Петра?
Заключение.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
Тема выпускной квалификационной работы раскрыта полностью.
Поставленные в начале работы задачи решены. Цель работы достигнута.
В школьном курсе математики диофантовы уравнения не изучаются, но на математических олимпиадах, конкурсах различного уровня и итоговой аттестации очень часто предлагаются задания, предполагающие решение какого-либо уравнения в целых числах. Поэтому важно познакомить учащихся с основными видами диофантовых уравнений и приемами их решения. Но еще более важной является задача развития устойчивого познавательного интереса учащихся к изучению отдельных предметов и вообще к учению как процессу, в первую очередь, творческому.
Результаты работы могут быть использованы учителями в школах, а также студентов ВУЗов.
Популярное:
- I I. Цели, задачи, результаты выполнения индивидуального проекта
- II. Основные задачи управления персоналом.
- II. Решить следующие ниже финансовые задачи на листе “Задачи”.
- II. Цели, задачи и предмет деятельности
- III. Задачи, решаемые организацией с помощью ИСУ и ИТУ.
- III. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ РАЙОННОЙ ОРГАНИЗАЦИИ ПРОФСОЮЗА
- III. Экономико-управленческие задачи производственной практики
- А. П. Петрова. «Сценическая речь» - Пути воплощения сверхзадачи
- Анализ использования основных фондов: задачи, объекты, этапы, источники информации, основные показатели.
- Анализ математических аксиом
- Анализ финансового состояния организации: задачи, методы, виды, последовательность, информационная база.
- Анализ финансовых результатов: задачи, объекты, этапы, источники информации, основные показатели.

