Задачи, аналогичные задачам С6 из ЕГЭ.
Данный и следующий параграфы на разделяются на уровни, так как соответствующие примеры предполагают хорошей подготовленности обучающихся.
В данном параграфе рассматриваются задачи типа С6, аналогичные тем, которые предлагались на Едином государственном экзамене по математике.
Пример 1. Найти все пары натуральных чисел  и
и  таких, что
таких, что  и выполнено равенство
и выполнено равенство  .
.
Решение. Ясно, что данное уравнение эквивалентно уравнению  . Рассмотрим общее уравнение
. Рассмотрим общее уравнение  (
(  и
и  различные действительные положительные числа). Преобразуем его следующим образом:
различные действительные положительные числа). Преобразуем его следующим образом:
 .
.
Рассмотрим функцию  тогда наше уравнение примет вид
тогда наше уравнение примет вид  Производная этой функции равна
Производная этой функции равна

Следовательно,  строго возрастает при
строго возрастает при  и строго убывает при
и строго убывает при  . Поэтому на каждом из этих промежутков функция
. Поэтому на каждом из этих промежутков функция  принимает любое своё значение ровно по одному разу. Это означает, что равенство
принимает любое своё значение ровно по одному разу. Это означает, что равенство  при
при  ≠
≠  возможно тогда и только тогда, когда
возможно тогда и только тогда, когда  и
и  принадлежат разным промежуткам. Но интервалу
принадлежат разным промежуткам. Но интервалу  принадлежат только два натуральных числа - это 1 и 2. При этом значение
принадлежат только два натуральных числа - это 1 и 2. При этом значение 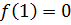 не принимается на интервале
не принимается на интервале  Таким образом, в натуральных числах исходное уравнение имеет решение только при
Таким образом, в натуральных числах исходное уравнение имеет решение только при 
Число  находим из уравнения:
находим из уравнения:
 ⇔
⇔  .
.
В силу приведённых выше рассуждений это решение будет единственным.
Ответ: 
Пример 2. Найти все тройки натуральных чисел  , удовлетворяющие уравнению
, удовлетворяющие уравнению
 .
. 
Решение. Возможны три случая. Если  , имеем:
, имеем:

Несложным перебором получаем, что либо  и тогда
и тогда  , либо
, либо 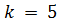 и
и  . Если
. Если  исходное уравнение преобразуется следующим образом:
исходное уравнение преобразуется следующим образом:



Последнее равенство невозможно, так как оба множителя (стоящие в квадратных скобках) больше единицы. И, наконец, если  , получаем, что
, получаем, что


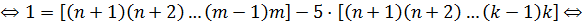
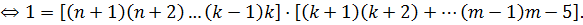
Полученное равенство также невозможно, поскольку число, стоящее в первой квадратной скобке, всегда больше единицы. Таким образом, решением задачи будут служить 
Ответ: 
Пример 3. Найти все натуральные  , для которых уравнение
, для которых уравнение 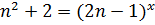 имеет хотя бы один рациональный корень
имеет хотя бы один рациональный корень  .
.
Решение. Пусть  рациональный корень данного уравнения. Преобразуем это уравнение следующим образом:
рациональный корень данного уравнения. Преобразуем это уравнение следующим образом:
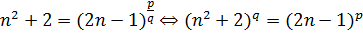 .
.
Ясно, что  при всех
при всех  , откуда следует, что
, откуда следует, что  при всех натуральных
при всех натуральных  . Поэтому будем считать числа
. Поэтому будем считать числа  положительными и взаимно простыми, причём
положительными и взаимно простыми, причём  . Пусть
. Пусть  Имеем:
Имеем:

Значит, дробь  является целым число. Разделим
является целым число. Разделим  на
на  в «столбик» с остатком:
в «столбик» с остатком:
 .
.
Следовательно, число  является делителем числа 9, поэтому возможны варианты
является делителем числа 9, поэтому возможны варианты  . При
. При  получаем, что
получаем, что  -нет решений в натуральных числах. При
-нет решений в натуральных числах. При  имеем
имеем  чего не может быть, так как в левой части не целое число. И наконец, при
чего не может быть, так как в левой части не целое число. И наконец, при  получаем уравнение
получаем уравнение  которое имеет решение в натуральных числах:
которое имеет решение в натуральных числах: 
Ответ: 
Пример 4. Найти все несократимые дроби  , представимые в виде
, представимые в виде  (запятая разделяет десятичные записи натуральных чисел
(запятая разделяет десятичные записи натуральных чисел  и
и  .
.
Решение. Пусть натуральные числа  взаимно просты, а десятичная запись числа а имеет
взаимно просты, а десятичная запись числа а имеет  знаков. Тогда условие задачи записывается в виде уравнения
знаков. Тогда условие задачи записывается в виде уравнения

из которого следует, в частности, что  . В силу взаимной простоты чисел
. В силу взаимной простоты чисел  число
число 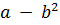 не имеет общих делителей ни с
не имеет общих делителей ни с  , ни с
, ни с  , следовательно, уравнение превращается в систему из двух уравнений
, следовательно, уравнение превращается в систему из двух уравнений

В силу все той же взаимной простоты чисел  (с учетом
(с учетом  ) последнему уравнению удовлетворяют только пары чисел
) последнему уравнению удовлетворяют только пары чисел  . Первая пара при подстановке дает для числа
. Первая пара при подстановке дает для числа  уравнение
уравнение  , которое не имеет решений. Если же
, которое не имеет решений. Если же  получаем, что
получаем, что 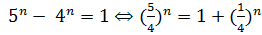
Так как левая часть полученного уравнения возрастает, а правая убывает, то это уравнение имеет не более одного корня, который угадывается:  , откуда
, откуда  .
.
Ответ:  .
.
Пример 5. Десятичная запись целого числа  , большего 9, должна состоять из различных цифр одной чётности, а само оно должно быть квадратом целого числа. Найти все такие числа
, большего 9, должна состоять из различных цифр одной чётности, а само оно должно быть квадратом целого числа. Найти все такие числа  .
.
Решение. Заметим сначала, что  - чётное число, так как при возведении любого нечётного числа, большего 3, в квадрат вторая цифра справа получается чётной. Действительно, квадрат любого нечётного числа оканчивается либо на 1, либо на 5, либо на 9 и должен давать остаток 1 при делении на 4, что не может произойти, если вторая справа цифра нечётная. Последней цифрой числа
- чётное число, так как при возведении любого нечётного числа, большего 3, в квадрат вторая цифра справа получается чётной. Действительно, квадрат любого нечётного числа оканчивается либо на 1, либо на 5, либо на 9 и должен давать остаток 1 при делении на 4, что не может произойти, если вторая справа цифра нечётная. Последней цифрой числа  не может быть 6. Если это так, то вторая справа цифра должна быть нечётной, иначе
не может быть 6. Если это так, то вторая справа цифра должна быть нечётной, иначе  будет давать остаток 2 при делении на 4, что также невозможно.
будет давать остаток 2 при делении на 4, что также невозможно.
Следовательно, последняя цифра числа  - это 4 (если последняя цифра числа есть 0, то и предпоследняя должна быть равна 0, что приводит к противоречию). Рассмотрим теперь возможные остатки при делении числа
- это 4 (если последняя цифра числа есть 0, то и предпоследняя должна быть равна 0, что приводит к противоречию). Рассмотрим теперь возможные остатки при делении числа  на 3. Полный квадрат при делении на 3 дает либо остаток 1, либо 0. Остатки при делении на 3 чисел 2, 4, 6, 8, 0 есть 2, 1, 0, 2, 0 соответственно. Так как любое число дает при делении на 3 тот же остаток, что и сумма его цифр, то число
на 3. Полный квадрат при делении на 3 дает либо остаток 1, либо 0. Остатки при делении на 3 чисел 2, 4, 6, 8, 0 есть 2, 1, 0, 2, 0 соответственно. Так как любое число дает при делении на 3 тот же остаток, что и сумма его цифр, то число  дает остаток 1 при различных комбинациях цифр 4, 6, 0 (4 - по-следняя цифра, могут входить не все цифры), а остаток 0 - при различных комбинациях цифр 4, 6, 8, 0 (в этом случае
дает остаток 1 при различных комбинациях цифр 4, 6, 0 (4 - по-следняя цифра, могут входить не все цифры), а остаток 0 - при различных комбинациях цифр 4, 6, 8, 0 (в этом случае  делится на 9, поэтому сумма цифр должна быть равна 18, цифра 0 может не входить, 4 - последняя цифра). В первом случае полным квадратом является число
делится на 9, поэтому сумма цифр должна быть равна 18, цифра 0 может не входить, 4 - последняя цифра). В первом случае полным квадратом является число  , во втором - число
, во втором - число  .
.
Ответ: 64, 6084.
Пример 6. Какое наибольшее число членов может иметь геометрическая прогрессия, все члены которой - различные натуральные числа, большие 340 и меньшие 520?
Решение. Без ограничения общности будем рассматривать только возрастающие геометрические прогрессии (если прогрессия убывающая, всегда можно положить первый член новой прогрессии равным последнему члену исходной, второй - предпоследнему и т.д., последний - ее первому члену). Знаменатель  такой геометрической прогрессии должен быть рационален как отношение двух натуральных чисел. Пусть
такой геометрической прогрессии должен быть рационален как отношение двух натуральных чисел. Пусть  , где
, где  несократимая дробь,
несократимая дробь,  первый член данной прогрессии,
первый член данной прогрессии,  - количество её членов. Докажем, что ответом к задаче является
- количество её членов. Докажем, что ответом к задаче является  . В качестве примера возьмём прогрессию, у которой
. В качестве примера возьмём прогрессию, у которой
 и
и 
Покажем, что для любой другой прогрессии, удовлетворяющей условиям задачи, всегда  .
.
Из неравенств  следует, что
следует, что 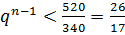 .Если
.Если  имеем
имеем

(каждый раз берём минимально возможное  , чтобы «уместить» как можно больше членов прогрессии). Значит, при всех таких
, чтобы «уместить» как можно больше членов прогрессии). Значит, при всех таких  количество членов прогрессии не превосходит 3. Пусть теперь
количество членов прогрессии не превосходит 3. Пусть теперь  . Так как числа
. Так как числа 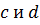 -взаимно простые, а числа
-взаимно простые, а числа  при
при  натуральные, то
натуральные, то  должно делиться без остатка на
должно делиться без остатка на  . В предположении
. В предположении  нужно найти в промежутке
нужно найти в промежутке  такое натуральное число, которое делилось бы нацело на куб натурального числа, большего либо равного 8. Ясно, что такое число только одно, это число 512, и оно соответствует уже построенной нами геометрической прогрессии.
такое натуральное число, которое делилось бы нацело на куб натурального числа, большего либо равного 8. Ясно, что такое число только одно, это число 512, и оно соответствует уже построенной нами геометрической прогрессии.
Следовательно, данная в условии задачи геометрическая прогрессия может иметь максимум 4 члена.
Ответ: 4 члена.
Пример 7. Найти все пары натуральных чисел  , которые удовлетворяют равенству
, которые удовлетворяют равенству  (в левой части стоит число, получаемое дописыванием десятичной записи числа
(в левой части стоит число, получаемое дописыванием десятичной записи числа  после десятичной записи числа
после десятичной записи числа  ).
).
Решение. При  данное уравнение принимает вид
данное уравнение принимает вид  и имеет решение
и имеет решение  . Если
. Если  и
и  является
является  - значным числом, то исходное уравнение преобразуется к виду
- значным числом, то исходное уравнение преобразуется к виду  и не имеет решений в целых числах. Далее будем считать, что
и не имеет решений в целых числах. Далее будем считать, что  2. Если
2. Если  , то в левой части уравнения стоит двузначное число, откуда следует неравенство
, то в левой части уравнения стоит двузначное число, откуда следует неравенство  . Ясно, что это неравенство выполняется только для следующих пар чисел:
. Ясно, что это неравенство выполняется только для следующих пар чисел: 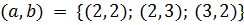 . Проверкой убеждаемся, что ни одна из этих пар не является решением задачи. Если же
. Проверкой убеждаемся, что ни одна из этих пар не является решением задачи. Если же  , а
, а  является
является  - значным числом, где
- значным числом, где  , то справедлива следующая оценка:
, то справедлива следующая оценка:
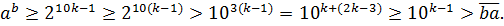
Следовательно, в этом случае исходное уравнение решений не имеет.
Пусть теперь  . Тогда для выполнения равенства необходимы условия:
. Тогда для выполнения равенства необходимы условия:  , так как иначе, если
, так как иначе, если  является -значным числом, а
является -значным числом, а  является
является  -значным числом, где
-значным числом, где  , имеем:
, имеем:
если  , то
, то

если  то
то

если  , то
, то

если k = 1, b = 2, m = 1, a > 32, то

Конечным перебором для всех пар  для которых
для которых  и
и  , получаем, что уравнению удовлетворяет всего одна пара
, получаем, что уравнению удовлетворяет всего одна пара  Таким образом, ответом к задаче будут служить две пары чисел
Таким образом, ответом к задаче будут служить две пары чисел 
Ответ: 
Пример 8. Каждое из чисел  умножают на каждое из чисел
умножают на каждое из чисел  и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все полученные 54 результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все полученные 54 результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Решение. Если все произведения взяты со знаком плюс, то их сумма максимальна и равна

Так как предыдущая сумма оказалась нечётной, то число нечётных слагаемых в ней - нечётно, причём это свойство всей суммы не меняется при смене знака любого её слагаемого. Поэтому любая из получающихся сумм будет нечётной, а значит, не будет равна нулю. Значение 1 сумма принимает, например, при такой расстановке знаков у произведений, которая получается при раскрытии следующих скобок:


Таким образом, наименьшая по модулю сумма, которую можно получить исходя из условий задачи, равна 1, а наибольшая сумма равна 4131.
Ответ: 1 и 4131.
Задачи для самостоятельного решения.
1. Найти все тройки натуральных чисел  ,
,  удовлетворяющие уравнению
удовлетворяющие уравнению  . Здесь
. Здесь 
2. Найти все натуральные  , для которых уравнение
, для которых уравнение  имеет хотя бы один рациональный корень
имеет хотя бы один рациональный корень  .
.
3. Рассматриваются наборы различных целых чисел, произведение которых равно 180. Для каждого такого набора рассматриваются арифметические прогрессии, состоящие из чисел этого набора. Из какого наибольшего количества членов может состоять такая арифметическая прогрессия?
4. Набор состоит из 41 натурального числа, среди которых есть числа 3, 5 и 7. Среднее арифметическое любых 34 чисел этого набора меньше 2.
а) Может ли такой набор содержать ровно 17 единиц?
б) Меньше 17 единиц?
в) Доказать, что в любом таком наборе есть несколько чисел, сумма которых равна 35.
5. Найти все пары натуральных чисел  , удовлетворяющие равенству
, удовлетворяющие равенству  (в левой части равенства стоит число, получаемое приписыванием десятичной записи числа а перед десятичной записью числа
(в левой части равенства стоит число, получаемое приписыванием десятичной записи числа а перед десятичной записью числа  ).
).
6. Какое наибольшее число членов может иметь геометрическая прогрессия, все члены которой - различные натуральные числа, большие 210 и меньшие 350?
7. Перед каждым из чисел 22, 23, ..., 26 и 50, 51, ..., 60 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 55 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Популярное:
- I I. Цели, задачи, результаты выполнения индивидуального проекта
- III. Задачи, решаемые организацией с помощью ИСУ и ИТУ.
- Анализ использования основных фондов: задачи, объекты, этапы, источники информации, основные показатели.
- Анализ финансового состояния организации: задачи, методы, виды, последовательность, информационная база.
- Анализ финансовых результатов: задачи, объекты, этапы, источники информации, основные показатели.
- Виды, задачи, формы организации делопроизводства в органах внутренних дел. Субъекты делопроизводства в ОВД и их обязанности
- Глава 1. Предмет, задачи, принципы и методы психологии
- Дошкольная педагогика: предмет, категории, задачи, источники, основные этапы в развитии дошкольной педагогики. Связь дошкольной педагогики с другими науками.
- Задачи, адресаты и особенности интернационального развития персонала
- Задачи, близкие к задаче о кратчайшем пути
- Задачи, использующие делимость целых чисел.

