
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Предмет электрохимии. Проводники первого и второго рода. Законы Фарадея.Стр 1 из 11Следующая ⇒
Предмет электрохимии. Проводники первого и второго рода. Законы Фарадея. Теория электролитической диссоциации Аррениуса. Закон разбавления Оствальда. Причины диссоциации. ПРЕДМЕТ ЭЛЕКТРОХИМИИ. Электрохимия является разделом физической химии, в котором изучаются законы взаимосвязи химических и электрических явлений. Основным предметом электрохимии являются процессы, протекающие на электродах при прохождении тока через растворы, - электродные процессы. Можно выделить два основных раздела электрохимии: термодинамику электродных процессов, охватывающую равновесные состояния систем электрод - раствор, и кинетику электродных процессов, изучающую законы протекания этих процессов во времени. Электрохимия изучает также теорию электролитов. Электрохимия имеет очень большое значение, т.к. закономерности электрохимии являются теоретической основой для разработки важных технических процессов - электролиза и электросинтеза, т.е. получения химических продуктов на электродах при прохождении тока через растворы (получение хлора и щелочей, получение и очистка цветных и редких металлов, электросинтез органических соединений). Важной областью практического применения электролиза является гальванотехника - электропокрытие металлами. Другая важная область техники, в основе которой лежат электрохимические процессы, - это создание химических источников тока (гальванических элементов, в том числе аккумуляторов), в которых химическая реакция используется как источник электрического тока. Большое развитие получили электрохимические методы химического анализа (электроанализ, кондуктометрия, потенциометрия, полярография и др.). Возникновение электрохимии как науки связано с именами Гальвани, Вольта и Петрова, которые на рубеже XVIII и XIX в. открыли и исследовали электрохимические (гальванические) элементы. Деви и Фарадей в первой половине XIX в. изучали электролиз. Быстрое развитие электрохимии в конце XIX в. связано с появлением теории электролитической диссоциации Аррениуса (1887) и с работами Нернста по термодинамике электродных процессов. Теория Аррениуса развита Дебаем и Гюккелем (1923), которые разработали электростатическую теорию. Для последних десятилетий характерно быстрое развитие электрохимической кинетики, изучение явлений перенапряжения, коррозии, гальванических покрытий и др.
ПРОВОДНИКИ ПЕРВОГО И ВТОРОГО РОДА. Твердые и жидкие проводники, прохождение через которые электрического тока не вызывает переноса вещества в виде ионов, называются проводниками первого рода. Электрический ток в проводниках первого рода осуществляется потоком электронов ( электронная проводимость ). К таким проводникам относятся твёрдые и жидкие металлы и некоторые неметаллы (графит, сульфиды цинка и свинца). Вещества, прохождение через которые электрического тока вызывает передвижение вещества в виде ионов ( ионная проводимость ) и химические превращения в местах входа и выхода тока (электрохимические реакции), называются проводниками второго рода. Типичными проводниками второго рода являются растворы солей, кислот и оснований в воде и некоторых других растворителях, расплавленные соли и некоторые твёрдые соли. Как правило, в проводниках второго рода электричество переносится положительными (катионы) и отрицательными (анионы) ионами, однако некоторые твёрдые соли характеризуются униполярной проводимостью, то есть переносчиками тока в них являются ионы только одного знака - катионы (например, в AgCl) или анионы (BaCl2, ZrO2+CaO, растворы щёлочных металлов в жидком аммиаке). Деление проводников в зависимости от типа проводимости (электронная или ионная) является условным. Известны твёрдые вещества со смешанной проводимостью, например Ag2S, ZnO, Cu2O и др. В некоторых солях при нагревании наблюдается переход от ионной проводимости к смешанной (CuCl). Проводники второго рода называются электролитами. Это могут быть чистые вещества или растворы. Часто электролитами называют вещества, растворы которых проводят электрический ток. Эти растворы называют растворами электролитов. ЭЛЕКТРОХИМИЧЕСКИЕ РЕАКЦИИ. Электрохимические реакции протекают на границе электрод (проводник первого рода) - электролит (проводник второго рода). Они вызваны невозможностью для электронов - носителей тока в электродах свободно двигаться в электролите. Эти реакции состоят в обмене электронами между электродом и ионами (молекулами) в растворе. На катоде электроны переходят от электрода к иону (или молекуле), на аноде - от иона (молекулы) к электроду, при этом ионы (молекулы) теряют или изменяют свой электрический заряд. Это - первичная электрохимическая реакция, продукты которой нередко вступают в дальнейшие реакции, не связанные непосредственно с переносом тока ионами. Примерами катодных реакций могут служить следующие реакции: Cu2+ + 2e ® Cu (1) Fe3+ + e ® Fe2+ (2) 2H3O+ + 2e ® H2(г) + 2H2O (3) На аноде могут протекать реакции типа: 4OH- ® O2 + 2H2O + 4e (4) Fe2+ ® Fe3+ + e (5) 2Cl- ® Cl2(г) + 2e (6) Zn ® Zn2+ + 2e (7) Материал электрода может участвовать в электрохимической реакции [реакция (7)], но может быть и инертным (остальные реакции). В последнем случае на поверхности электрода могут выделяться металлы [реакция (1)] или газы [реакции (3, 4, 6)]. Наконец, электрохимическая реакция может протекать и при отсутствии перехода ионов из раствора к электроду и обратно. В этих случаях перенос электричества осуществляют только электроны, но у поверхности электрода в растворе ионы изменяют свою валентность [реакции (2) и (5)]. Совокупность двух электрохимическихреакций, из которых одна протекает на катоде, а другая - на аноде, даёт химическую реакцию электролиза или реакцию, протекающую в электрохимическом элементе: Cu2+ + 2Cl- ® Cu(т) + Cl2 (1) + (6) 2H3O+ + 2OH- ® 1/2 O2 + H2 + 3H2O (3) + 1/2 (4) или H2O ® 1/2 O2 + H2
ЗАКОНЫ ЭЛЕКТРОЛИЗА (ЗАКОНЫ ФАРАДЕЯ). Поскольку прохождение электрического тока через электрохимические системы связано с химическими превращениями, между количеством протекающего электричества и количеством прореагировавших веществ должна существовать определенная зависимость. Она была открыта Фарадеем и получила свое выражение в первых количественных законах электрохимии, названных впоследствии законами Фарадея. Первый закон Фарадея. Количества веществ, превращённых при электролизе, пропорциональны количеству электричества, прошедшего через электролит. Dm = kэIt = kэq Dm – количество прореагировавшего вещества; kэ – некоторый коэффициент пропорциональности; q – количество электричества, равное произведению силы тока I на время t. Если q = It = 1, то Dm = kэ, т.е. коэффициент kэ представляет собой количество вещества, прореагировавшего в результате протекания единицы количества электричества. Коэффициент kэ называется электрохимическим эквивалентом. Второй закон Фарадея отражает связь, существующую между количеством прореагировавшего вещества и его природой: при постоянном количестве прошедшего электричества массы различных веществ, испытывающие превращение у электродов (выделение из раствора, изменение валентности), пропорциональны химическим эквивалентам этих веществ : Dmi /Ai = const Можно объединить оба закона Фарадея в виде одного общего закона : для выделения или превращения с помощью тока 1 г-экв любого вещества (1/z моля вещества) необходимо всегда одно и то же количество электричества, называемое числом Фарадея (или фарадеем ). Dm = Точно измеренное значение числа Фарадея F = 96484, 52 ± 0, 038 к / г-экв Таков заряд, несомый одним грамм-эквивалентом ионов любого вида. Умножив это число на z (число элементарных зарядов иона), получим количество электричества, которое несёт 1 г-ион. Разделив число Фарадея на число Авогадро, получим заряд одного одновалентного иона, равный заряду электрона: e = 96484, 52 / (6, 022035× 1023) = 1, 6021913× 10-19 к Законы, открытые Фарадеем в 1833 г., строго выполняются для проводников второго рода. Наблюдаемые отклонения от законов Фарадея являются кажущимися. Они часто связаны с наличием неучтённых параллельных электрохимических реакций. Отклонения от закона Фарадея в промышленных установках связаны с утечками тока, потерями вещества при разбрызгивании раствора и т.д. В технических установках отношение количества продукта, полученного при электролизе, к количеству, вычисленному на основе закона Фарадея, меньше единицы и называется выходом по току. При тщательных лабораторных измерениях для однозначно протекающих электрохимических реакций выход по току равен единице (в пределах ошибок опыта). Закон Фарадея точно соблюдается, поэтому он лежит в основе самого точного метода измерения количества электричества, прошедшего через цепь, по количеству выделенного на электроде вещества. Для таких измерений используют серебряный или медный, а также йодный и газовый кулонометры ( кулонометрия ).
Теория электролитов ТЕОРИЯ ЭЛЕКТРОЛИТИЧЕСКОЙ ДИССОЦИАЦИИ АРРЕНИУСА. Для электролитов понижение температуры замерзания и осмотическое давление значительно больше соответствующих величин для неэлектролитов. В уравнение для осмотического давления p Вант-Гофф ввел эмпирический коэффициент i > 1, физический смысл которого стал понятен с появлением теории электролитической диссоциации: p = icRT Теория электролитической диссоциации была предложена Аррениусом (1884-1887), развившим отдельные высказывания ряда ученых. Основные положения теории Аррениуса: Соли, кислоты, основания при растворении в воде и некоторых других полярных растворителях частично или полностью распадаются (диссоциируют) на ионы. Эти ионы существуют в растворе независимо от того, проходит через раствор электрический ток или нет. Вследствие этого число независимо движущихся частиц растворенного вещества больше, чем при отсутствии диссоциации, а величины коллигативных свойств растворов возрастают прямо пропорционально числу частиц. Наряду с процессом диссоциации в растворе идет обратный процесс - ассоциация ионов в молекулы. В качестве меры электролитической диссоциации Аррениус ввел величину степени диссоциации a, определяемую как долю молекул, распавшихся на ионы: a = Для любой обратимой реакции электролитической диссоциации: Кn+Аn- Û n+Кz+ + n-Az- сумма n+ + n- равна общему числу n ионов, образующихся при диссоциации одной молекулы, которое равно коэффициенту Вант-Гоффа i:
Определив коэффициент i, можно по этому уравнению вычислить степень диссоциации a, если известна величина n. По мере увеличения разведения коэффициент Вант-Гоффа приближается к простому целому числу (2, 3, 4 - в зависимости от числа ионов, образующихся из одной молекулы вещества). Диссоциация растворенных веществ на ионы подчиняется тем же законам химического равновесия, что и др. реакции: Кд = где Кд - константа диссоциации, выраженная через концентрации. Диссоциация сильных электролитов равна 100% или почти 100%, так что концентрации ионов можно считать равными молярности растворенного вещества, умноженной на z. При диссоциации слабого электролита устанавливается равновесие между недиссоциированными молекулами и ионами. Рассмотрим простейший пример, когда молекула распадается только на два иона: СН3СООН Û СН3СОО- + Н+ с - aс aс aс Кд = Последнее равенство является простейшей формой закона разведения Оствальда (1888). Чем больше Кс, тем выше степень диссоциации. Т.о., величина Кс может служить мерой силы кислоты, т.е. мерой кислотности. Для электролитов средней силы (Н3РО4 - первая ступень, Са(ОН)2, СНСl2СООН) значения Кс лежат в пределах от 10-2 до 10-4; для слабых электролитов (СН3СООН, NН4ОН) Кс = 10-5 - 10-9; при Кс < 10-10 электролит считается очень слабым (Н2О, С6Н5ОН, С6Н5NН2, НСN). Если a очень мала, то ее величиной можно пренебречь по сравнению с 1, и формула примет вид: Кс = a2с; a = Если электролит распадается больше чем на два иона, то зависимость Кс от a усложняется: СаCl2 Û Ca2+ + 2Cl- с (1- a) aс 2aс Кс = При малой a: a = Величина Кс является постоянной только для очень разбавленных растворов, коэффициенты активности которых можно считать равными 1. Вообще же Кс (как и a) зависит от концентрации раствора; Кс иногда еще называют классической константой диссоциации. Кс (a) зависит также от температуры: зависимость Кс слабых кислот в воде проходит через максимум. Это можно объяснить влиянием двух противоположно направленных воздействий. С одной ст., всякая диссоциация протекает с поглощением тепла, и, следовательно, при повышении Т равновесие должно смещаться в сторону большей диссоциации. С др. ст., при повышении Т диэлектрическая проницаемость воды, служащей растворителем, уменьшается, а это способствует воссоединению ионов. Кс максимальна при той Т, при которой влияние второго фактора начинает преобладать. Обычно изменение Кд с повышением Т невелико.
ПРИЧИНЫ ЭЛЕКТРОЛИТИЧЕСКОЙ ДИССОЦИАЦИИ. Твердые вещества, при растворении которых в воде и других полярных растворителях образуются электролиты, являются, как правило, кристаллическими телами, имеющими ионные или близкие к ионным решётки. В чисто ионных решётках не существует молекул вещества. Ионы противоположных знаков, составляющие такую решётку, связаны между собой большими электростатическими силами. При переходе ионов в раствор энергии электростатического взаимодействия ионов в решётке противопоставляется энергия взаимодействия ионов с дипольными молекулами растворителя, который втягивает ионы решётки в раствор. При этом ионы окружаются молекулами растворителя, образующими вокруг иона сольватную (в частном случае - гидратную) оболочку. Энергия взаимодействия ионов различных знаков, перешедших в раствор и окружённых сольватными оболочками, уменьшается по сравнению с энергией их взаимодействия в решётке обратно пропорционально диэлектрической проницаемости растворителя D в соответствии с законом Кулона: E = - где z1 и z2 - число элементарных зарядов катиона и аниона; r - расстояние между катионом и анионом. Если энергия взаимодействия ионов с растворителем становится соизмеримой с энергией ионов в кристаллической решётке, то происходит растворение с диссоциацией. Надо помнить при этом, что при растворении должен уменьшиться изобарный потенциал G системы, а внутренняя энергия (и энтальпия) может как уменьшаться, так и увеличиваться (отрицательная и положительная теплоты растворения). Взаимодействие дипольных молекул растворителя с элементами кристаллической решётки может привести к образованию электролита даже при растворении веществ, имеющих молекулярную решётку, решётку промежуточного типа или находящихся в газообразном состоянии (атомы в молекулах газа связаны ковалентно). Ясно, что для осуществления электролитической диссоциации определяющую роль играет взаимодействие ионов с растворителем (в водных растворах - гидратация, в общем случае - сольватация). На важное значение гидратации ионов впервые указали И.А.Каблуков и В.А.Кистяковский. Они положили начало развитию теории электролитов в направлении, которое указывал Д.И.Менделеев, то есть объединили так называемую сольватную теорию и физическую теорию Вант-Гоффа - Аррениуса. Связь между диэлектрической проницаемостью D растворителя и его способностью образовывать растворы, проводящие электрический ток, отмечалась давно. Вода, диэлектрическая проницаемость которой D = 81 при 18°C, а также HCN (D=107 при 25°C) и HCOOH (D=57 при 25°С) принадлежат к растворителям, вызывающим сильную диссоциацию. Низшие спирты и кетоны, уксусная кислота, пиридин имеют диэлектрические проницаемости в пределах 20-35 и также способны образовывать электролиты, хотя и в меньшей степени, чем вода. Кроме величины диэлектрической проницаемости важное значение имеет взаимодействие молекул растворителя с молекулами растворённого вещества. Это взаимодействие нередко приводит к образованию новых молекул или молекулярных комплексов, которые в данном растворителе способны диссоциировать на ионы. Лекция 41 I II III
|
Числа переноса определяются из соотношений:
t+ = 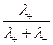 =
= 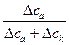 , t- =
, t- = 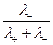 =
= 
и в рассмотренном примере t+(H+) » 5/6 = 0, 83, t-(Cl-) » 1/6 = 0, 17, откуда видно, что количество ионов данного типа, участвующих в переносе электричества, никак не связано с количеством ионов, передавших свой заряд электроду.
 Определенные по методу Гитторфа числа переноса называются кажущимися числами переноса ; они не являются истинными, т.к. этот метод не учитывает сольватации ионов. Измеряемые в методе Гитторфа концентрации определяются не только количеством катионов и анионов, но и количеством растворителя, перенесенного этими ионами в виде сольватных оболочек. Оболочки ионов разных знаков неодинаковы по величине.
Определенные по методу Гитторфа числа переноса называются кажущимися числами переноса ; они не являются истинными, т.к. этот метод не учитывает сольватации ионов. Измеряемые в методе Гитторфа концентрации определяются не только количеством катионов и анионов, но и количеством растворителя, перенесенного этими ионами в виде сольватных оболочек. Оболочки ионов разных знаков неодинаковы по величине.
Существование рассмотренного эффекта можно легко установить, прибавив к электролиту недиссоциирующее на ионы вещество, например, сахар или мочевину. Учитывая изменение концентрации прибавленного неэлектролита при определении чисел переноса, можно ввести поправку на перенос воды из анодного пространства в катодное в виде сольватных оболочек и найти истинные числа переноса t+ и t-. Но обычно в значения чисел переноса, найденные опытным путем по методу Гитторфа, поправки не вводятся.
Зависимость чисел переноса от концентрации обычно невелика. Однако в некоторых случаях число переноса сильно изменяется с концентрацией и может оказаться равным нулю и даже меньше нуля (например, для концентрированного раствора CdI2 t+ < 0). Это можно объяснить образованием комплексных анионов (CdI42-).
Влияние температуры на числа переноса незначительно. Во многих случаях числа переноса при повышении температуры приближаются к 0, 5, т.е. подвижности катиона и аниона становятся почти одинаковы.
Растворы одной и той же соли в разных растворителях имеют различные числа переноса; это объясняется, в основном, различной степенью сольватации катионов и анионов в зависимости от растворителя.
Лекция 43
Классификация электродов. Электроды первого и второго рода. Электроды сравнения. Газовые электроды. Амальгамные электроды. Окислительно-восстановительные электроды, правило Лютера. Хингидронный электрод, измерение рН.
ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ.
Одна из основных особенностей электрохимической системы состоит в пространственном разделении участников протекающей в ней реакции. Общая реакция распадается здесь на две частные реакции, каждая из которых совершается на отдельном электроде. В соответствии с этим ЭДС электрохимической системы также должен представлять собой сумму двух электродных потенциалов: Е = j1 + j2.
Скачок потенциала на границе электрод-раствор (как и разность потенциалов между двумя точками, находящимися в различных фазах) экспериментально измерить невозможно. Величина такого скачка потенциала может быть рассчитана теоретически, но лишь в том случае, если точно известно строение границы раздела двух фаз. Структура границы между электродом и раствором изучена до сих пор недостаточно.
Экспериментально можно измерить лишь общее значение Е цепи, т.е. только сумму электродных потенциалов. Для устранения неопределённости величин j необходимо ввести дополнительное условие - принять потенциал какого-либо электрода равным 0 и относить к нему значения потенциалов всех других электродов. В этом случае потенциалы электродов даются в некоторой условной шкале и их значения зависят от природы электрода, выбранного за основу шкалы.
Нернст предложил считать условным нулём потенциал водородного электрода при концентрации водородных ионов в растворе, равной 1, и давлении газообразного водорода 1 атм. Эта условная шкала потенциалов называется водородной шкалой. В настоящее время применяется главным образом условная водородная шкала, в которой при всех Т за ноль выбран потенциал стандартного водородного электрода. Она отличается от первоначальной водородной шкалы Нернста тем, что в ней вместо единичных концентраций и давления выбраны единичная активность и летучесть. Это условие позволяет определять потенциалы электродов в водородной шкале при любых Т, однако при каждой Т потенциал водородного электрода может быть иным, то есть условный нуль не будет одним и тем же при разных Т.
Т.о., электродным потенциалом электрода называется ЭДС элемента, составленного из этого электрода (справа) и стандартного водородного электрода (слева), например:
(+) Pt ï H2 ç H+, aq ç ç Zn2+ ç Zn (-)
ЭДС этого элемента (jZn2+ç Zn) отрицательна (-0, 763 В при активности ионов цинка в растворе, равной 1, - это и есть стандартный электродный потенциал цинка). Чтобы найти электродный потенциал меди, нужно составить элемент:
(-) Pt ï H2 ç H+, aq ç ç Cu2+ ç Cu (+)
Здесь ЭДС цепи (jCu2+ç Cu) положительна (+0, 337 В при активности ионов меди, равной 1, - стандартный электродный потенциал меди).
Целесообразно в схеме полуэлемента записывать сочетание электрод + раствор иона в том порядке, который имеется в записи элемента, составленного из стандартного водородного электрода и данного; именно для записанного таким образом электрода следует приводить электродный потенциал с соответствующим знаком. При обратной записи следует изменить знак потенциала, например:
(1) Zn2+, aq ç Zn; j = -0, 763 B, (2) Zn ç Zn2+, aq; j = +0, 763 B
Только первый тип записи приводит к тем знакам величин j, которые соответствуют электродным потенциалам. Величины, соответствующие записи (2), не следует называть электродными потенциалами, но ими можно пользоваться при подсчете ЭДС цепи (для электродов, расположение которых в схеме цепи является обратным расположению их в сочетании с водородным электродом), например:
(-) Zn ç Zn2+, aq ç Cu2+, aq ç Cu (+)
+0, 763 В +0, 337 В
Е = j1 + j2 = 0, 763 + 0, 337 = 1, 110 В
Диффузионный потенциал, возникающий на границе растворов ZnSO4-CuSO4, усложняет расчет.
Диффузионный потенциал возникает на границе двух растворов, отличающихся друг от друга и качественно, и количественно. Причина его возникновения - неодинаковая подвижность ионов электролита и наличие градиента их концентрации.
На границе двух растворов имеется некоторый переходный слой, где состав меняется от раствора I до раствора II и от раствора II до раствора I; в этом переходном слое локализуется диффузионный потенциал. Ионы, обладающие большей подвижностью, диффундируют в более разбавленный раствор с большей скоростью, и поверхность соприкосновения двух растворов заряжается знаком этих ионов со стороны более разбавленного раствора и обратным знаком - со стороны концентрированного. Образуется диффузный двойной электрический слой с соответствующим скачком потенциала. Возникающая разность потенциалов будет ускорять движение медленно движущегося иона и замедлять движение быстро движущегося, пока не наступит стационарное состояние, при котором скорости диффундирующих ионов сравняются. Дальнейшее взаимное удаление зарядов прекращается; установившаяся в пограничном слое разность потенциалов и носит название диффузионного потенциала.
Диффузионный потенциал - неравновесный. Точно его рассчитать в общем случае невозможно.
При измерениях невысокой точности можно существенно снизить диффузионный потенциал на границе двух растворов, включив между ними солевой мостик - концентрированный электролит (насыщенный KCl или NH4NO3) с числами переноса ионов, близкими к 0, 5. Резкое уменьшение диффузионного потенциала в этом случае связано с тем, что ионы концентрированного раствора проводят практически весь ток в зонах соприкосновения; один диффузионный потенциал заменяется при введении солевого мостика двумя потенциалами меньшей величины, часто противоположными по знаку.
С этой же целью используется введение индифферентной соли во все растворы цепи.
Зависимость величины электродного потенциала от концентрации (активности) вещества в электролите может быть установлена методами термодинамики. На электроде Мn+ç М с равновесным потенциалом j протекает электрохимическая реакция:
Мn+, aq + ne = М
Это - реакция дегидратации иона металла и включения его в кристаллическую решетку.
Для равновесного процесса при постоянных Р и Т убыль изобарного потенциала равна максимальной полезной работе А¢ - работе электрического тока:
А¢ = -DG = nFj
При переходе 1 г-иона металла из раствора в электрод изменение изобарного потенциала равно разности химических потенциалов вещества в двух фазах: в растворе (m¢ ) и в электроде (m¢ ¢ ):
DG = m+¢ ¢ - m+¢
При Р, Т = const в электроде неизменного состава (чистый металл)
m+¢ ¢ = m+о = const
В растворе m+¢ = m+¢ о + RT ln a+
m+¢ о - химический потенциал иона в растворе в стандартном состоянии; эта величина при заданной Т постоянна.
DG = m+o - m+¢ o - RT ln a+
j = - (m+o - m+¢ o)/nF +  ln a+
ln a+
Первый член правой части уравнения при постоянных Р и Т - величина постоянная (для металлического электрода эта величина практически не зависит от давления). Можно обозначить ее символом jо:
j = jо +  ln a+ (1)
ln a+ (1)
В разбавленном растворе вместо активностей можно подставить концентрации (а+ ® m+, c+, N+) в зависимости от выбора меры концентрации и соответственно стандартного состояния для активности, например:
j = jо +  ln m+ (2)
ln m+ (2)
Уравнение (2) было выведено Нернстом (1888) иным путем. Это уравнение, а также более общее уравнение (1) носит название уравнения электродного потенциала Нернста.
jо - это потенциал электрода относительно раствора с активностью соответствующих ионов, равной 1. Он называется стандартным электродным потенциалом и зависит от температуры.
Считая g¢ ± » g¢ + и m+ » m±, для бинарного одно-одновалентного электролита (n = 1) имеем:
j = jо +  ln a± = jо +
ln a± = jо +  ln m± +
ln m± +  ln g¢ ±
ln g¢ ±
Подставляя значение F и переходя от натуральных логарифмов к десятичным, получаем для n = 1 и Т = 298 К:
j = jо + 0, 0591 lg m± g¢ ±
СТАНДАРТНЫЙ ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ. Значение стандартного электродного потенциала не зависит от активностей участников электродной реакции и представляет собой константу, характерную для данного электрода. Стандартные потенциалы (табличные величины) отнесены к 25оС; их значения при других Т могут быть найдены по температурным коэффициентам, также сведенным в таблицу.
Стандартные потенциалы используются при решении многих проблем, связанных с химическим равновесием в растворах.
Любой электрод, расположенный ниже в ряду стандартных электродных потенциалов (т.е. более положительный), находится в более окисленном состоянии, чем электрод, расположенный выше (пример: элемент Даниэля-Якоби). Если из двух таких электродов составить электрохимическую систему, то на «нижнем» будет протекать реакция восстановления (Cu), а на «верхнем» - реакция окисления (Zn). Процесс идет в том же направлении, если активные вещества обоих электродов находятся в непосредственном контакте друг с другом и реакция протекает по химическому пути. Равновесие в системе наступит в тот момент, когда потенциалы двух электродных реакций сделаются одинаковыми. Такое состояние достигается при определенном соотношении активностей участников реакции, отвечающем константе ее равновесия (примеры: системы Ce3+, Ce4+ и Fe2+, Fe3+; Fe2+, Fe3+ и Sn2+, Sn4+; ряд активности металлов).
КЛАССИФИКАЦИЯ ЭЛЕКТРОДОВ.
Если на электроде протекает частная реакция
nA A +... + nF = nL L +...
то потенциал электрода определяется уравнением:
j = jо +  ln
ln 
т.е. при заданных Т и Р определяется (кроме jо, который является константой) активностями веществ, участвующих в электродной реакции. Характер влияния активностей компонентов раствора на значение j связан с природой электродной реакции и лежит в основе классификации электродов. Принято различать электроды первого рода, второго рода, газовые, окислительно-восстановительные и некоторые специальные типы электродов.
ЭЛЕКТРОДЫ ПЕРВОГО РОДА.
Электроды первого рода можно схематически представить в виде Мn+ ê М (если электрод - металл) или в виде Меn- ê Ме (если электрод - металлоид). Электродную реакцию записывают как
Mn+ + ne ® M или Me + ne ® Men-
 =
=  +
+  ln
ln  =
=  + 2, 303
+ 2, 303  lg
lg 
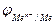 =
=  +
+  ln
ln 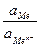 =
=  - 2, 303
- 2, 303  lg
lg 
(т.к. активность чистого твердого вещества при заданной Т постоянна и можно принять ее условно равной 1).
Из уравнений следует, что потенциал электрода первого рода зависит от активности лишь одного вида ионов; эти ионы называются потенциалоопределяющими. В случае металлических электродов первого рода такими ионами являются катионы металла, а в случае металлоидных электродов - анионы металлоида. Примеры металлических электродов: металл, погруженный в раствор своей соли (Ag в растворе AgNO3 - Ag+ ê Ag; Cu в растворе CuSO4 - Cu2+ ê Cu). Пример металлоидных электродов первого рода - селеновый электрод Se2- ê Se.
Металлические электроды первого рода имеют большое практическое значение и легче реализуются, чем металлоидные.
ЭЛЕКТРОДЫ ВТОРОГО РОДА.
Электроды второго рода представляют собой полуэлементы, состоящие из металла, покрытого слоем его труднорастворимого соединения (соли, оксида, гидроксида) и погруженного в раствор, содержащий тот же анион, что и труднорастворимое соединение электродного металла. Схематически электрод второго рода можно представить как An- ê MA ê M, а протекающую в нем реакцию
MA + ne = M + An-
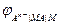 =
=  + 2, 303
+ 2, 303  lg
lg 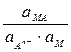 =
=  - 2, 303
- 2, 303  lg
lg 
(учитывая, что активности металла и твердого соединения МА постоянны).
Т.о., потенциал электрода второго рода определяется активностью анионов труднорастворимого соединения электродного металла. Однако электроды второго рода обратимы и по отношению к катионам электродного металла:
ПРМА = 
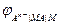 =
=  - 2, 303
- 2, 303  lg ПРМА + 2, 303
lg ПРМА + 2, 303  lg
lg  =
=
 + 2, 303
+ 2, 303  lg
lg  =
= 
Из сопоставления потенциалов соответствующих электродов первого и второго рода можно найти ПР труднорастворимых солей.
Потенциалы электродов второго рода легко воспроизводимы и устойчивы, поэтому эти электроды часто применяют в качестве электродов сравнения, по отношению к которым измеряют потенциалы других электродов. Наиболее важны в практическом отношении каломельные, ртутно-сульфатные, хлорсеребряные, ртутнооксидные и сурьмяные электроды.
КАЛОМЕЛЬНЫЙ ЭЛЕКТРОД. Это ртуть, покрытая пастой из смеси каломели со ртутью, находящаяся в контакте с раствором KCl:
Cl- ê Hg2Cl2 ê Hg
Электродная реакция: Hg2Cl2 + 2e = Hg + 2 Cl-
jкал = jокал - 2, 303  lg
lg 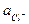
При 25оС jкал = + 0, 2678 - 0, 059 lg 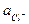
jкал определяется активностью ионов Cl-. Наиболее часто употребляются каломельные полуэлементы, в которых концентрация KCl - насыщенный раствор, 1.0 М или 0.1 М. Каломельные электроды, особенно насыщенный, удобны тем, что диффузионный потенциал, возникающий на границе данного раствора с насыщенным KCl, незначителен и во многих случаях его можно не принимать во внимание.
Последнее изменение этой страницы: 2016-03-15; Просмотров: 2345; Нарушение авторского права страницы