Работа при равновесном и неравновесном изменении объема системы

Пусть газ, заключенный в цилиндр и закрытый сверху невесомым подвижным поршнем, находится в равновесии. Это значит, что давление газа p равно внешнему давлению среды (рис. 24).

Р и с.24

Поло­жим, что газ бесконечно медленно (равновесно) расширился за счет полученного тепла и поршень переместился на из положения АВ в положение . Вычислим работу, которую при этом совершил газ. Работа эта заключается в том, что газ при расширении преодолевает внешнее давление , под которым он находится. По определению работы

(2.4.1)

где – внешняя сила давления, преодолеваемая газом, а – увеличение объема газа при его расширении, – пло­щадь поршня.

Работа расширения, совершаемая газом, при конечном изменении объема

(2.4.2)

Ясно, что работа расширения против сил внешнего давления произво­дится только тогда, когда изменяется объем тела 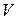и когда внеш­нее давление не равно нулю. Если же 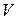сохраняется постоян­ным, то какие бы изменения ни претерпевали любые другие параметры, характеризующие состояние газа (температура, давление, внутренняя. энергия и т. д.), работа расширения всегда будет равна нулю. С другой стороны, если объем газа изменяется, но внешнее давление все время равно нулю как это имеет место при расшире­нии газа в вакуум, то работа расширения тоже равна нулю. Поэтому с точки зрения возможности совершения газом работы против внешнего давления параметр 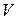является жестко связанным с этим давлением, как говорят, сопряжен с ним.

Знак работы определяется знаком Так как абсолютное давление – существенно положительная величина, то при расширении работа производится газом над внешней средой и, как видно из соотношений (3.4.1–3.4.2), положительна, при сжатии работа совершается внешней средой над газом и, как видно из тех же соотношений, отрицательна.

Формулы (2.4.1–2.4.2) справедливы не только для газов, но и для жидких и твердых тел. Рассмотрим, например, твердое тело, помещенное в жидкую или газообразную среду, которая при от­сутствии внешних полей оказывает одинаковое давление на любые участки поверхности этого тела (рис. 25)

Р и с. 25

Постоянство давления легко объясняется тем, что молекулы среды, находящейся в сос­тоянии равновесия, движутся по всем направлениям с одинаковой ве­роятностью, с одинаковыми средними скоростями и на каждую единицу поверхности тела приходится в среднем одинаковое число ударов молекул одинаковой силы (закон Паскаля). При наличии внешнего поля силы тяжести давление также можно считать постоянным на всей поверхности тела, если размеры его таковы, что можно пренебречь изменениями гидростатического давления.

Пусть при расширении тела элементарные участки его поверхности переместились по нормали к ним на расстояние . Тогда работа на i-м участке

Полная работа тела по увеличению объема на

что совпадает с формулой (2.4.1).

Чтобы процесс был равновесным, он должен протекать бесконечно медленно. При этом давление газа и внеш­нее давление среды отличаются на бесконечно малую величину, т. е. для равновесных про-цессов справедливо равенство

(2.4.3)

Поэтому формулы (2.4.1–2.4.2) для равновесного процесса приобре-тают вид:

, (2.4.4)

(2.4.5)

где – давление газа (внутреннее давление в системе), которое может быть вычислено из уравнения состояния, например, из уравне­ния Менделеева – Клапейрона, если газ идеальный. Особо отметим, что формулы (2.4.4–2.4.5) справедливы только для равновесных процессов. Если процесс неравновесный, то давление газа отличается от давле­ния окружающей среды на конечную величину. В этом случае расширение газа протекает с конечной скоростью, внешнее давление меньше давления газа на конечную величину и, соответственно, полезная работа при неравновес­ном процессе меньше полезной работы при равновесном процессе, т. е.

. (2.4.6)

При неравновесном сжатии, наоборот, внешнее давление больше давле­ния газа, поэтому и затраченная работа на сжатие больше, чем в слу­чае равновесного процесса, т. е.

(2.4.7)

Весьма важные соотношения (2.4.6–2.4.7) поясним на следующем простом опыте. Будем рассматривать расширение и сжатие газа, находящегося в цилиндре под поршнем, который нагружен гирьками одинакового ве­са (внешнее давление). Пусть точка А (рис. 25, а) отме-чает исходное равновесное состояние газа.

После снятия гирьки резко уменьшается внешнее давление, затем происходит быстрое увеличение объема и газ приходит в новое равновесное состояние, обозначенное точкой 1. После снятия второго грузика давление и объем вновь изменятся скачком (также неравновесно) и газ опять придет в состояние равновесия, соответствующее точке 2.

а б

Р и с. 26

Дальнейшее снятие грузиков приведет газ в состояние, характеризуемое точкой В. Таким образом, в ре­зультате неравновесного процесса газ расширился от объема до , совершив при этом полезную работу , величина кото­рой определяется площадью между нижней ступенчатой линией АВ и осью абсцисс (на рис. 26, а эта площадь заштрихована).

Проведем обратный процесс сжатия газа, постепенно нагружая поршень гирьками. Этот процесс изобразится на рис. 26, а верхней ступенчатой линией ВА, площадь между нею и осью абсцисс будет равна затраченной работе на сжатии газа. Как видно из рис. 26, а > . Разность - равна площади, заклю­ченной между верхней и нижней ступенчатыми линиями.

Если теперь уменьшить вес каждого грузика вдвое, оставив об­щий их вес неизменным, и провести процессы расширения и сжатия газа с новыми грузиками, то полезная работа , как видно из рис. 26, б, несколько увеличится, а затраченная на сжатие газа работа , наоборот, уменьшится. Уменьшится и их разность.

Если вес грузиков уменьшить настолько, что внешнее давление будет изменяться на бесконечно малую величину, то ступенчатые линии, соответствующие расширению и сжатию газа, практически сольются с гладкой линией АВ. При этом полезная работа при расширении газа будет максимальной, а затраченная ра­бота на сжатие газа будет минимальной; их разность будет стремится к нулю. Все это будет свидетельствовать о том, что процессы расширения и сжатия газа окажутся бесконечно медленными, т. е. равновесными.

Таким образом, при неравновесных процессах работа расширениявсегда меньше а работа сжатия больше, чем при равновесных процессах.

В дальнейшем мы ограничимся рассмотрением тех задач, в которых работа, совершаемая системой или над системой, связана только с си­лами давления и изменения объема, т. е. работу будем вычислять, пользуясь формулами (2.4.4–2.4.5).

Нетрудно видеть, что работа, определяемая по этим формулам, не является функцией состояния, так как величина интеграла

(2.4.8)

определяемая площадью между кривой и осью абсцисс, зависит не только от координат точек 1 и 2(рис. 27), но и от пути перехода из 1B2.

Р и с. 27

Например, работа по пути 1А2 больше работы по пути 1В2, потому что по пути 1А2 работа соверша­ется на всем пути против большего внешнего давления (для равновесного процесса, напомним, ), чем на пути 1В2. Если работа, совершаемая системой при переходе из одного состояния в другое, зависит от пути перехода, то подынтегральное выражение в (2.4.8) не является полным дифференциалом, т. е. величина просто бесконечно малая величина. Тогда из первого закона термодинамики сразу же следует, что и бесконечно малое коли­чество теплоты не является полным дифференциалом, т. е. коли­чество теплоты не представляет собой функцию состояния. Заметим, од­нако, что разность есть полный дифференциал, т. к. внутренняя энергия – это функция состояния.

Таким образом, работа и количество теплоты – это функции процесса, происходящего с системой, а не только начального и конеч­ного состояний системы. Внутренняя же энергия не зависит от того, каким про­цессом система приведена в данное состояние, и определяется только координатами этого состояния.

 

Теплоемкость

Для вычисления количества теплоты, получаемой или отдаваемой системой при переходе из одного состояния в другое, используется понятие теплоемкости. Это одна из важнейших характеристик вещества. Различают молярную и удельную теплоемкости.

Молярной теплоемкостью называют количество тепла, которое необходимо сообщить одному молю, вещества, чтобы повысить его тем­пературу на 1К:

(2.5.1)

Удельной теплоемкостью называют количество тепла, которое нужно передать 1 кг вещества, чтобы повысить его температуру на 1К:

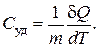(2.5.2)

В последних формулах – элементарное количество тепла, пере­данное веществу, – изменение его температуры, вызванное этим теплом, и – число молей и масса вещества соответственно.

Из формул (2.5.1–2.5.2) нетрудно получить связь между молярной и удельной теплоемкостями:

(2.5.3)

где – молярная масса. В дальнейшем, в основном, будем исполь­зовать молярную теплоемкость, которую будем называть просто тепло­емкостью.

Элементарное количество теплоты находится из выражения (2.5.1)

(2.5.4)

Количество теплоты, получаемое системой при нагревании от температуры до температуры ,

(2.5.5)

Из опыта известно, что теплоемкость в общем случае зависит от температуры. Поэтому часто при вычислении количества тепла исполь­зуют понятие средней теплоемкости . При этом количество теп­ла

(2.5.6)

где величину находят, используя теорему о среднем из матема­тического анализа:

(2.5.7)

Если же теплоемкость постоянна в интервале температур , то из выражения (2.5.5)

(2.5.8)

Теплоемкость, как собственное физическое свойство вещества, зависит от его природы (химического состава). Для заданного же вещества тепло­емкость существенным образом зависит от термодинамического процесса, в результате которого происходит передача тепла веществу и переход его из состояния с одной температурой в состояние с другой темпера­турой, т. е. теплоемкость есть функция процесса. Например, при изо­термическом процессе система получает тепло а темпе­ратура все время сохраняется постоянной, т. е. , следователь­но, на основании выражения (2.5.1) имеем бесконечное значение теп­лоемкости для изотермического процесса . При адиаба­тическом процессе система не получает и не отдает тепла хотя его температура изменяется 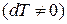, поэтому теплоемкость любых веществ при адиабатическом процессе равна нулю .

Зависимость теплоемкости от процесса объясняется тем, что коли­чество тепла , входящее в определение теплоемкости, не являет­ся функцией состояния, а зависит от пути перехода (процесса) системы из одного состояния в другое. Таким образом, у всякого вещества имеется бесконечное множество теплоемкостей, т. е. столько, сколько имеется путей перехода из одного состояния в другое. Чтобы устранить эту неоднозначность, сравнение теплоемкостей веществ производят при каком-нибудь заданном процессе. Обычно различают теплоемкости при постоянном объеме и теплоемкость при постоянном давлении , если в процессе нагревания поддерживаются постоянными соответ-ственно объем вещества или давление. Причем для любых веществ . В самом деле, при их изохорическом нагревании работа си-стемой не совершается. Поэтому все подводимое тепло, согласно первому закону термодинамики, идет на увеличение его внутренней энергии, т. е. на повышение его температуры. Если же давление системы при нагревании остается постоянным, то она должна расширяться (иначе давление будет расти), совершая внешнюю работу. В этом случае не все тепло, подводимое к системе, идет на изменение внутренней энергии, а часть этого тепла затрачивается на совершение работы. Следовательно, при постоянном давлении требуется большее количество теплоты для нагревания 1 моля вещества на 1К, чем при постоянном объеме.

Как мы знаем, внутренняя энергия веществ, не подвергнутых действию внешних полей, является функцией двух переменных : зависимость от температуры учитывает суммарную кинетическую энер-гию молекул, а от объема – суммарную потенциальную энергию их взаимо­действия.

Подставляя приращение внутренней энергии

(2.5.9)

в выражение (2.3.9), получим

. (2.5.10)

Подставив количество теплоты (2.5.10) в (2.5.1), получим

. (2.5.11)

 

Откуда находим теплоемкости при постоянном объеме и постоянном

давлении

, (2.5.12)

^. (2.5.13)

Как видно из выражений (2.5.12–2.5.13), для нахождения и необходимо располагать явным видом двух функций: – внутренней энергии и – уравнением состояния вещест­ва. Указанные функции не могут быть найдены теоретически методами термодинамики; их заимствуют либо из статистической теории, либо определяют опытным путем. Для идеального газа эти функции нам известны (2.2.4; 1.9.3):

, (2.5.14)

. (2.5.15)

Подставив (2.5.14–2.5.15) в (2.5.12–2.5.13), получим

, (2.5.16)

. (2.5.17)

Таким образом, для идеального газа теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме на величину , которая численно равна работе при изобарическом нагревании 1 моля идеального газа на 1К. Для отношения теплоемкостей получим

. (2.5.18)

Из формул (2.5.16–2.5.17) видно, что теплоемкости и для идеального газа не зависят от температуры. Значения теплоемкостей, полученные из формул (2.5.16–2.5.17), и эксперимен­тальные данные для одноатомных и многих двухатомных газов почти совпадают (в случае двухатомных газов лишь при температурах не очень сильно отлича-ющихся от комнатной). Для трех­атомных и многоатомных газов различие между теоретическими и опытны­ми данными теплоемкостей весьма существенны. Эти расхождения могут быть устранены лишь с помощью квантовой теории.

В заключение этого параграфа отметим, что теплоемкость является положительной величиной , если при получении тепла система разогревается и, наоборот, если система, отдавая тепло , охлаждается . Однако теплоемкость может быть и отрицательной . Это, как видно из формулы (2.5.1), наблюдается в двух слу­чаях:

1) при получении тепла система охлаждается ,

2) при отдаче тепла система разогревается .

Оба случая легко объясняются при помощи первого закона термоди-нами­ки, записанного в следующем виде:

. (2.5.19)

В первом случае газ производит работу расширения в коли­честве большем, чем количество теплоты , которое подво­дится к газу в процессе расширения . В этом случае на производство работы помимо тепла, подведенного к газу, расходуется и некоторое количество его внутренней энергии. Хотя к газу и подводится тепло, но оно целиком превращается в работу, а убыль внутренней энергии газа ведет к снижению температуры.

Во втором случае работа, производимая над газом при его сжатии , оказывается по абсолютной величине большей, чем ко­личество отдаваемого им тепла . С учетом знаков количества теплоты и работы равенство (2.5.19) принимает вид:

(2.5.20)

где уже и . Поэтому в этом случае, как видно из (2.5.20), внутренняя энергия системы увеличивается , а значит, ее температура растет, несмотря на то, что газ отдает теплоту. Подобный процесс происходит в некоторых звездах: гравитационные силы при сжатии звезды совершают работу большую, чем излучаемое ей тепло, поэтому звезда разогрева­ется, несмотря на то, что она излучает теплоту.

Наконец, обратим внимание на размерность теплоемкости. В сис­теме СИ ее размерностью, как видно из формулы (2.5.1), является

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Популярное:

1. AT : химич. Природа, строение, свойства, механизм специфического взаимодействия с АГ
2. AVC достигают макс. величины при этом объеме
3. Aбстрактные классы, используемые при работе с коллекциями
4. D триггеры, работающие по фронту.
5. D.3. Системы эконометрических уравнений
6. E) может быть необъективным, сохраняя беспристрастность
7. E) Способ взаимосвязанной деятельности педагога и учащихся, при помощи которого достигается усвоение знаний, умений и навыков, развитие познавательных процессов, личных качеств учащихся.
8. Else write('не принадлежит')
9. else write('не принадлежит')
10. Gerund переводится на русский язык существительным, деепричастием, инфинитивом или целым предложением.
11. I. Общие обязанности машиниста перед приёмкой состава в депо.
12. I. Понятие и система криминалистического исследования оружия, взрывных устройств, взрывчатых веществ и следов их применения.