Перевод чисел из одной системы счисления в другую
Перевод чисел из десятичной системы счисления в другую позиционную
Как мы уже отмечали, человек привык работать в десятичной системе счисления, а ЭВМ ориентирована на двоичную систему. Поэтому общение человека с машиной невозможно без создания простых и надёжных алгоритмов перевода чисел из одной системы в другую и наоборот. Итак, как осуществить перевод чисел из десятичной системы в двоичную? Допустим, надо перевести число 11 в двоичную систему счисления. Разделим 11 на 2. Получим частное 5 и остаток 1. Следовательно, в двоичной записи числа 11 последняя цифра равна 1. Для нахождения второй цифры разделим найденное нами частное 5 снова на 2. Получим частное 2 и остаток 1. Следовательно, вторая цифра с конца в двоичной записи числа 11 тоже равна 1. Частное 2 снова делим на 2. Получим 1 и 0 в остатке. Полученная 1 и есть первая цифра в двоичной записи числа 11. Остаток от последнего деления 0 - вторая цифра.
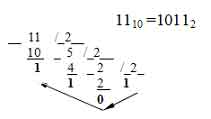 Если необходимо преобразовать нецелое число - десятичную дробь, то производим следующие действия: 1. Целую часть числа преобразовываем в двоичную систему способом, описанным выше. 2. Дробную часть необходимо преобразовывать умножением на основание системы, в которую мы переводим число.
Если необходимо преобразовать нецелое число - десятичную дробь, то производим следующие действия: 1. Целую часть числа преобразовываем в двоичную систему способом, описанным выше. 2. Дробную часть необходимо преобразовывать умножением на основание системы, в которую мы переводим число.
 В результате умножения дробной части - числа 0, 7 на основание системы - число 2 получим 1, 4. Целую часть данного числа (цифру 1) выделяем, а дробную часть - число 0, 4 снова умножаем на 2. Очевидно, что процесс перевода числа 0, 7 может продолжаться бесконечно. Действительно, за шесть шагов мы можем получить число 0, 101100, а за семь шагов получили бы 0, 1011001, которое является более точным представлением числа 0, 7 в двоичной системе. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа. В результате перевода получим ответ:
В результате умножения дробной части - числа 0, 7 на основание системы - число 2 получим 1, 4. Целую часть данного числа (цифру 1) выделяем, а дробную часть - число 0, 4 снова умножаем на 2. Очевидно, что процесс перевода числа 0, 7 может продолжаться бесконечно. Действительно, за шесть шагов мы можем получить число 0, 101100, а за семь шагов получили бы 0, 1011001, которое является более точным представлением числа 0, 7 в двоичной системе. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа. В результате перевода получим ответ:
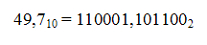 Для перевода десятичных чисел в другие позиционные системы счисления пользуются теми же правилами, лишь меняется лишь основание системы, в которую надо перевести числа.
Для перевода десятичных чисел в другие позиционные системы счисления пользуются теми же правилами, лишь меняется лишь основание системы, в которую надо перевести числа.
 Перевод чисел из двоичной системы счисления в системы, родственные двоичной и обратно.
Большие числа в двоичной системе счисления имеют очень громоздкие записи. Конечно, можно перевести число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоёмки. На помощь приходят системы, родственные двоичной - восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме. Системами счисления родственными двоичной считаются такие системы, основания которых являются значением степени числа 2. Например, четверичная, восьмеричная и шестнадцатеричная системы счисления являются системами, родственными двоичной.
Перевод чисел из двоичной системы счисления в системы, родственные двоичной и обратно.
Большие числа в двоичной системе счисления имеют очень громоздкие записи. Конечно, можно перевести число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоёмки. На помощь приходят системы, родственные двоичной - восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме. Системами счисления родственными двоичной считаются такие системы, основания которых являются значением степени числа 2. Например, четверичная, восьмеричная и шестнадцатеричная системы счисления являются системами, родственными двоичной.
 Для перевода чисел из двоичной системы счисления в системы, родственные двоичной, необходимо выполнить следующие действия: 1.Разбить число на некоторое количество разрядов, равное степени числа 2 основания системы, в которую переводим. 2.Если в старших и младших разрядах после разбиения не хватает знаков, то добавить их нулями. 3.По таблице определить значение пары, триады, тетрады и т.п. разрядов, записанных в двоичной системе счисления, соответственно значению в той системе, в которую переводим. Например, дано число 1111010111010, 0111, записанное в двоичной системе счисления. Для перевода его в восьмеричную систему счисления разобьём число на триады (т.к. основание числа 2 равно 3), начиная от запятой, вправо и влево: 1.111.010.111.010, 011.1. Разбиение показано точками. В старшей и младшей триадах не хватает разрядов. Дополним их нулями: 001.111.010.111.010, 011.100. По таблице определим восьмеричные цифры, соответствующие триадам. Получается восьмеричное число 17272, 34. Рассмотрим ещё один пример: дано число 1111010111010, 0111, записанное в двоичной системе счисления. Для перевода его в шестнадцатеричную систему счисления разобьём число на тетрады (т.к. основание числа 2 равно 4): 1.1110.1011.1010, 0111. В старшей тетраде не хватает разрядов. Дополним их нулями: 0001.1110.1011.1010, 0111. По таблице определим шестнадцатеричные знаки, соответствующие тетрадам. Получается шестнадцатеричное число 1EBA, 7. Пусть дано то же число. Для перевода его в четверичную систему счисления разобьём число на пары (т.к. основание числа 2 равно 2): 1.11.10.10.11.10.10, 01.11. В старшей паре не хватает одного разряда. Дополним его нулём: 01.11.10.10.11.10.10, 01.11. Определим четверичные цифры, соответствующие парам. Получается четверичное число 1322322, 13.
Как осуществить обратный перевод:
Пусть дано число 73, 62, записанное в восьмеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру числа запишем в виде триады из 0 и 1, соответствующей значению восьмеричной цифры в двоичной системе счисления: 111.011, 110.010.
Для перевода чисел из двоичной системы счисления в системы, родственные двоичной, необходимо выполнить следующие действия: 1.Разбить число на некоторое количество разрядов, равное степени числа 2 основания системы, в которую переводим. 2.Если в старших и младших разрядах после разбиения не хватает знаков, то добавить их нулями. 3.По таблице определить значение пары, триады, тетрады и т.п. разрядов, записанных в двоичной системе счисления, соответственно значению в той системе, в которую переводим. Например, дано число 1111010111010, 0111, записанное в двоичной системе счисления. Для перевода его в восьмеричную систему счисления разобьём число на триады (т.к. основание числа 2 равно 3), начиная от запятой, вправо и влево: 1.111.010.111.010, 011.1. Разбиение показано точками. В старшей и младшей триадах не хватает разрядов. Дополним их нулями: 001.111.010.111.010, 011.100. По таблице определим восьмеричные цифры, соответствующие триадам. Получается восьмеричное число 17272, 34. Рассмотрим ещё один пример: дано число 1111010111010, 0111, записанное в двоичной системе счисления. Для перевода его в шестнадцатеричную систему счисления разобьём число на тетрады (т.к. основание числа 2 равно 4): 1.1110.1011.1010, 0111. В старшей тетраде не хватает разрядов. Дополним их нулями: 0001.1110.1011.1010, 0111. По таблице определим шестнадцатеричные знаки, соответствующие тетрадам. Получается шестнадцатеричное число 1EBA, 7. Пусть дано то же число. Для перевода его в четверичную систему счисления разобьём число на пары (т.к. основание числа 2 равно 2): 1.11.10.10.11.10.10, 01.11. В старшей паре не хватает одного разряда. Дополним его нулём: 01.11.10.10.11.10.10, 01.11. Определим четверичные цифры, соответствующие парам. Получается четверичное число 1322322, 13.
Как осуществить обратный перевод:
Пусть дано число 73, 62, записанное в восьмеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру числа запишем в виде триады из 0 и 1, соответствующей значению восьмеричной цифры в двоичной системе счисления: 111.011, 110.010.
 Рассмотрим ещё один пример: дано число 7В3, Е6, записанное в шестнадцатеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру шестнадцатеричного числа запишем в виде тетрады из 0 и 1, соответствующей значению знака в двоичной системе счисления: 0111.1011.0011, 1110.0110.
Рассмотрим ещё один пример: дано число 7В3, Е6, записанное в шестнадцатеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру шестнадцатеричного числа запишем в виде тетрады из 0 и 1, соответствующей значению знака в двоичной системе счисления: 0111.1011.0011, 1110.0110.
 Перевод чисел из р-ичной позиционной системы счисления в десятичную.
Все позиционные системы счисления, о которых мы говорили выше, строятся по одному общему принципу. Выбирается некоторое число р - основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, т.е. произвольное число в системе счисления с основанием р имеет вид:
Перевод чисел из р-ичной позиционной системы счисления в десятичную.
Все позиционные системы счисления, о которых мы говорили выше, строятся по одному общему принципу. Выбирается некоторое число р - основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, т.е. произвольное число в системе счисления с основанием р имеет вид:
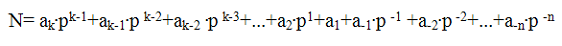 Если необходимо перевести двоичное число 1011011, 11 в десятичную систему, воспользуемся этой формулой. Основание системы р=2, к - коэффициент, указывающий количество знаков в числе влево от запятой, к=7; а - знаки числа с соответствующими им коэффициентами.
Если необходимо перевести двоичное число 1011011, 11 в десятичную систему, воспользуемся этой формулой. Основание системы р=2, к - коэффициент, указывающий количество знаков в числе влево от запятой, к=7; а - знаки числа с соответствующими им коэффициентами.
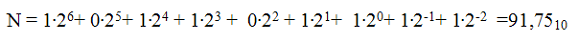 Воспользуемся формулой для перевода шестнадцатеричного числа ВF, 1D в десятичную систему. Основание системы р=16, к=2.
Воспользуемся формулой для перевода шестнадцатеричного числа ВF, 1D в десятичную систему. Основание системы р=16, к=2.
 Пусть необходимо перевести восьмеричное число 254, 262 в десятичную систему. Основание системы р=8, к=3
Пусть необходимо перевести восьмеричное число 254, 262 в десятичную систему. Основание системы р=8, к=3
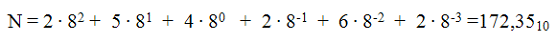 
| |

