Плоскости общего и частного положения ⇐ ПредыдущаяСтр 8 из 14Следующая ⇒

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1) Плоскость не перпендикулярная, и не параллельная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный a_П1; - фронтальный a_П2; - профильный a_П3).

Следы плоскости общего положения пересекаются попарно на осях в точках a_x, a_y, a_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рисунок 5.6).

Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2) Плоскость перпендикулярная горизонтальной плоскости проекций ( a^P₁ ), называется горизонтально-проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом.

 

 

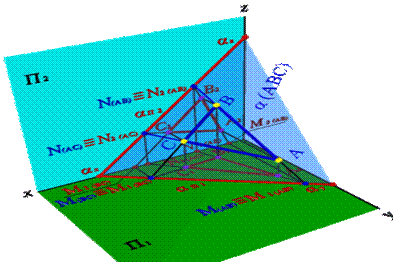
Рисунок 5.6. Плоскость общего положения

 

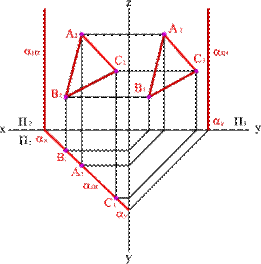
Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рисунок 5.7).

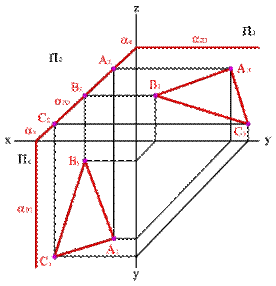
3) Плоскость перпендикулярная фронтальной плоскости проекций ( a^П₂ )- фронтально-проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом a_П2 (рисунок 5.8).

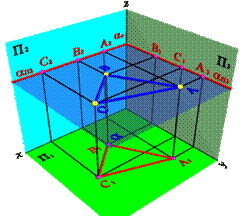
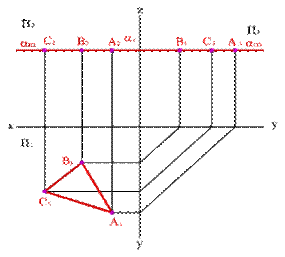
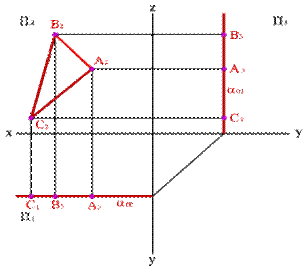
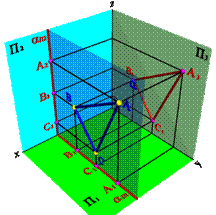
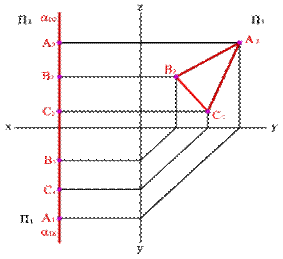
4) Плоскость перпендикулярная профильной плоскости ( a^П₃ ) – профильно-проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рисунок 5.9).

Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:

а) модель	б) эпюр
Рисунок 5.7. Горизонтально-проецирующая плоскость
а) модель	б) эпюр
Рисунок 5.8. Фронтально-проецирующая плоскость
а) модель	б) эпюр
а) модель	б) эпюр
Рисунок 5.10. Горизонтальная плоскость
а) модель	б) эпюр
Рисунок 5.11. Фронтальная плоскость

 

а) модель		б) эпюр
Рисунок 5.12. Профильная плоскость   Внимание! Проанализируйте изученное! Составьте конспект по рассмотренной теме в табличной форме, давая сравнительную характеристику различных положений плоскостей относительно плоскостей проекций (опишите свойства плоскостей общего и частного положения). Контрольные вопросы 1 Что такое плоскость? 2 Перечислите и изобразите графические способы задания плоскости на комплексном чертеже. 3 Перечислите характеристики свойства плоскости. 4 Дайте графические и физические характеристики плоскостям: горизонтально-проецирующей, фронтально-проецирующей, профильно-проецирующей. 5 Какую плоскость называют плоскостью уровня? 6 Какую плоскость называют горизонтальной? Фронтальной? Профильной? Изобразите их на эпюре и на наглядном чертеже. 7 Какую плоскость называют проецирующей? 8 Какие проецирующие плоскости вы знаете? Изобразите их на эпюре и на наглядном чертеже.

 

 

ЛЕКЦИЯ №6

Точка и прямая в плоскости. Главные линии плоскости.

Взаимное положение плоскостей

Цель лекции: уметь различать взаимное положение прямой и плоскости в пространстве и на комплексном чертеже, решать задачи на взаимное положение двух плоскостей.

· Точка в плоскости.

· Прямая в плоскости. Главные линии в плоскости.

· Взаимное положение двух плоскостей.

 

Точка в плоскости

 

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рисунок 6.1). Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).

Задача. Дано: плоскость a ( а, в) и проекция точки А₂. Требуетсяпостроить проекцию А₁ если известно, что точка А лежит в плоскости в, а.

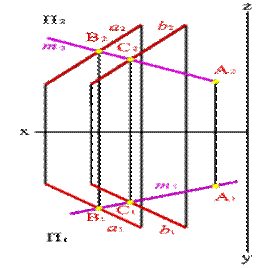
Через точку А₂ проведем проекцию прямой m₂, пересекающую проекции прямых a₂ и b₂ в точках С₂ и В₂ ( СÎ a, BÎ a Þ mÎ a). Построив проекции точек С₁ и В₁, определяющие положение m₁, находим горизонтальную проекцию точки А ( А₁Î m₁, mÎ a Þ АÎ a).

Через точку А₂ проведем проекцию прямой m₂, пересекающую проекции прямых a₂ и b₂ в точках С₂ и В₂ ( СÎ a, BÎ aÞ mÎ a). Построив проекции точек С₁ и В₁, определяющие положение m₁, находим горизонтальную проекцию точки А ( А₁Î m₁, m Î aÞ АÎ a).

Горизонтальный след α _П1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след α _П3 – прямая соединяющая точки ( α _y и α _z ) пересечения горизонтального и фронтального следов с осями.

а) модель	б) эпюр
Рисунок 6.1. Точка, принадлежащая плоскости

Прямая в плоскости

 

Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в, последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a (рисунок 6.2)

 

	Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямаяа лежит в плоскости a, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость a.
Рисунок 6.2. Метод вспомогательных секущих плоскостей

Таким образом, возможны три случая относительного расположения прямой и плоскости:

· Прямая принадлежит плоскости.

· Прямая параллельна плоскости.

· Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости.

Рассмотрим каждый случай:

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Популярное:

1. I. ПОЛОЖЕНИЯ И НОРМЫ ДЕЙСТВУЮЩЕГО ЗАКОНОДАТЕЛЬСТВА, В ОБЛАСТИ ОРГАНИЗАЦИИ ПРОТИВОПОЖАРНОЙ ПРОПАГАНДЫ И ОБУЧЕНИЯ НАСЕЛЕНИЯ МЕРАМ ПОЖАРНОЙ БЕЗОПАСНОСТИ
2. II. Основные положения по организации практики
3. XIV. Заключительные положения
4. Анализ месторасположения промышленного предприятия
5. Анализ общего качества уравнения регрессии.
6. Анализ финансового положения
7. Аналитическая психология и психотерапия К. Юнга, основные положения.
8. Англо-американская правовая семья, или семья «общего права»
9. Будьте центром своей Вселенной – и действуйте во имя общего блага
10. В условиях покоя только часть крови циркулирует в сосудах, которая составляет от общего количества крови
11. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
12. Влияние данного положения или движения на органы