
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Числовые характеристики вариационного ряда
Пусть выборка задана рядом распределения частот признака Х:
где
Тогда средним арифметическим выборки называют величину
Дисперсией или мерой рассеяния значений признака Х по отношению к его среднему арифметическому называют величину
А корень квадратный из дисперсии называют средним квадратическим отклонением
Отношение среднего квадратического отклонения к среднему арифметическому выборки, выраженное в процентах, называется коэффициентом вариации V.
Эмпирической функцией распределения относительных частот называют функцию, определяющую для каждого значения относительную частоту события (X < x), т.е. где тх – число вариант, меньших х, а п – объем выборки. Пример. Пусть статистическое распределение выборки имеет вид:
Тогда ряд распределения относительных частот признака Х имеет вид:
Найдем характеристики Решение. Среднее арифметическое признака Х равно
Дисперсия признака Х равна
тогда σ (X) = V = Ответ:
* * *
389. Из 100 контрольных работ по математике 23 оценено на «отлично».
390. По цели произведено 40 выстрелов. Относительная частота попаданий в мишень оказалась равной 0, 85. Найдите число попаданий в мишень.
391. Выберите отрывок текста, содержащий 200 букв. Найдите относительную частоту появления а) гласной буквы; b) буквы ф; с) буквы а.
392. Из полного набора костей домино наудачу извлекается одна кость. Чтобы оценить вероятность появления «дубля», повторим этот опыт 100 раз, каждый раз перемешивая кости. Вычислить относительную частоту появления «дубля» и сравните ее с вероятностью появления этого события.
393. Постройте полигон относительных частот по данным распределения студентов 1 курса по размерам обуви:
394. Поставьте опыт: 10 студентов по 25 раз вынимают наудачу кость из полного набора домино и каждый раз записывают выпавшее число очков. С помощью 250 данных статистической совокупности составьте статистическое распределение выборки. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот, составить ряд относительных частот.
395. Путем опроса получены следующие данные о возрасте (число полных лет) 25 студентов первого курса:
396. Составить статистическое распределение вероятности студентов по возрасту. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот и составить ряд относительных частот.
397. Путем опроса получены следующие данные о времени, которое в среднем тратят 30 студентов первого курса на дорогу до института:
Составить статистическое распределение вероятности студентов по времени, затраченному на дорогу до института. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот и составить ряд относительных частот.
398. Выписать ряд данных измерения, состоящего из всех букв первого предложения, расположенного на этой страницы задачника. Полученные буквы занумеруйте в соответствии с местом, занимаемым ими в русском алфавите. Составить статистическое распределение вероятности полученного числового ряда. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот и составить ряд относительных частот. 399. Анализ выполнения контрольных работ по математике 25 студентами группы студентов 1 курса дал следующие результаты: 3, 5, 4, 3, 3, 4, 3, 2, 5, 4, 3, 4, 2, 5, 5, 3, 3, 4, 3, 5, 4, 4, 3, 2, 4. Составить статистическое распределение вероятности полученного числового ряда. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот и составить ряд относительных частот.
400. Дана исходная таблица распределения 25 абитуриентов по числу баллов, полученных ими при сдачи ЕГЭ:
Составить статистическое распределение абитуриентов по числу баллов. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот и составить ряд относительных частот.
401. Имеются данные о количестве студентов в 20 группах некоторого факультета:
Составить статистическое распределение абитуриентов по числу баллов. Найти размах варьирования, моду, медиану вариационного ряда, построить полигон частот и составить ряд относительных частот.
402. Подбросьте 100 раз игральную кость и найдите относительные частоты следующих событий: а) выпадение двух очков; b) выпадение шести очков; с) выпадение четного числа очков; d) выпадение числа очков, кратного трем. Сравните относительные частоты с вероятностями появления этих событий.
403. Вычислите значения
404. Вычислите значения
405. Вычислите значения
406. Вычислите значения
407. Вычислите значения
408. Путем опроса п студенток соберите данные о размере их обуви, составьте исходную таблицу и дайте общую характеристику рассматриваемого признака: а) составьте дискретный вариационный ряд признака Х; b) составить ряд относительных частот признака Х; с) составьте эмпирическую функцию распределения относительных частот d) найдите точечные характеристики вариационного ряда: среднее арифметическое, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
409. Путем опроса п студенток соберите данные об их росте, составьте исходную таблицу и дайте общую характеристику рассматриваемого признака: а) составьте дискретный вариационный ряд признака Х; b) составить ряд относительных частот признака Х; с) составьте эмпирическую функцию распределения относительных частот d) найдите точечные характеристики вариационного ряда: среднее арифметическое, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Ответы
Глава 1
8.М
Глава 2
119.а) 19, b) 41, с) -17.120.а) 1, b) cos (α + β ). 122. а) 1, b) 0. 123. а) -93, b) 114. 124. а) -683, b) 98. 125. а) -632, b) -55. 126. а) 9, b) -25. 127. а) (1, -1, 1, 1), b) нет решения. 128. а) (1, 2, 2, -1), b) (с-2, с, 1+с, с). 129. а) (4, -1, 3, 2), b) (-1, 3, -2, -1). 130. а) (-21, 27, 7, -15), b) (1, -2, -1, 2). 131. а) (-3, 0, 1, 1), b) (0, 1, 4, -2). 132. а) (1, 1, -1, -1), b) (2, 1, 0, -1). 133. а) (-3; -5), b) (2; -1). 134. а) (7; -2), b) (0; 3). 135. а) (1; 6), b)
Глава 3 141.а) 1, b)
Глава 4 158.а) y'(-3) = -1, b) y'(0) = -2. 159. а) y' = 3 cos (3x +2), b) y' = -5 sin (5x – 1). 160. а) y'(-1) = -
Глава 5
212.а) ln |tg
Глава 6 244. g)y = Ctg
Глава 7 265. 8. 266. 21. 268. 72. 269. 63. 270. 216. 272. 16. 273. 10; 21. 278. 27. 279. 232. 280. 81; 27. 281. 1024. 282. 48. 283. 20. 284. 500. 285. 720; 420. 286. 7200. 288. 2520. 289. 66. 291. 1365. 292. 24310. 293. 3003. 294. 220. 296. 172800. 297. 6000. 298. a) 2268; b)2381. 300. 2000. 320. ≈ 0, 4. 321. 0, 3. 323.
376.
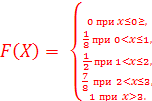 ; b) M (X) = 1, 5: D (X) = 0, 75 ; b) M (X) = 1, 5: D (X) = 0, 75
378. а) P(1, 75 < X < 2) = 0, 5; b) p = 0, 16. 379. P(-1< X < 0) = 0, 75. 380. Список использованной литературы
1. Виленкин Н.Я., Потапов В.Г. Задачник практикум по теории вероятностей с элементами комбинаторики и математической статистики. М.: Просвещение, 1985. 2. Выгодский М.Я. Справочник по высшей математике. М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2004. 3. Давыдов В.А., Коровкин Б.П. Сборник задач по математическому анализу. М.: Просвещение, 1973. 4. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. М.: АСТ: Астрель, 2005.
Оглавление
Популярное:
|
Последнее изменение этой страницы: 2016-09-01; Просмотров: 1381; Нарушение авторского права страницы