Математические задачи принятия сложного решения.

⇐ ПредыдущаяСтр 42 из 51Следующая ⇒

Встает задача определения такого сост-я с-мы, при котором знач-я всех локальных показ-лей будут наилучшими по вып-ю всех показ-лей одновременно, т.е. сост-ю, оптимальному для достиж-я любой цели. Такие планы наз-ся компромиссно- оптимальными, а задача их нах-я- принятие сложного реш-я.

Проблема согласов-я локальных и глобальных интересов в эконом-х с-мах сводится к след. задачам:

1. задачи векторной оптимиз-ии,

Согласлвание однородных критериев происходит путем:

1.1 с помощью критериев оптимальности по Паретто

1.2 в ранжировании критериев по важности, выделении одного из них в качестве главного, а остальные задаются в качестве дополнительных ограничений

2. многокритериальные (многоцелев.) задачи,

Это задачи поиска оптим-го реш-я, удовлетворяющего несколько несводимым друг к другу критериям. Один из подходов к реш-ю таких задач- опр-е целевой ф-ии с-мы (ф-ии полезности) в виде взвешенной суммы локальных целевых ф-ий, приведенных к безразмерному виду. Знач-я весовых коэф-в м. найти, например, на основе Метода Парных Сравнений.

3. многоэкстремальные.

Существует другая классификация задач. Выделяют 4-е типа задач:

1. Оптимизация на множестве целей

2. Оптимизация на множестве объектов. Качество оценивается векторным критерием, составленным из частных критериев.

3. Оптимизация на множестве условия функционирования

4. Оптимизация на множестве этапов функционирования. Интервал времени разбивается на несколько этапов, качество управления на каждом этапе оценивается частными критериями, а на множестве этапов – общим векторным критерием.

В задачах 2, 3, 4 обычно критерии имеют единую размерность. Как правило для 1 типа задач локальные критерии имеют разную размерность. В этом случае приведение локальных критериев к одной размерности осуществляется путем нормирования критериев т.е. приведением их к безразмерному виду.

Наиболее распространенным способом свертки неск. локальных критериев оптимальности L_i(x) в одну целевую функцию F(x) являются:

Критерий справедливости абсолютной уступки F₁(x)=Σ f_iL_i⁽^p⁾→ max

Критерий справедливой относительной уступки F₂(x)=П[L_i⁽^p⁾]^fi→ max

L_i⁽^p⁾ – нормированная, локальная цел. Функция

f_i – коэф. важности свертки i-й целевой функции

Многокритериальные задачи.

Во всех динамических системах с переходом от отдел. звеньев к более крупным системам действует закон перехода от количества к качеству.

В частности фирмы, следуя миссии, определяют: оптимальный уровень обслуживания путем балансировки рисков и доходов. Компромиссное решение определяет наилучшее соотношение между ценами и уровнем обслуживания, между риском и прибылью.

Аналогично решается задача определения оптимального размера поставки.

Пусть затраты состоят из 2-х составляющих С=Схр+Сзак

Схр – затраты на хранение, Сзак – затраты на выполнение заказа

Пусть D – годовое количество товара в шт., С1 – затраты на выполнение одного заказа, С2 – затраты на хранение единицы продукции, Q – искомый размер заказа.

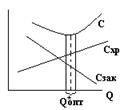
С=0, 5QC2+C1*D/Q

Где 0, 5QC2=Схр, C1*D/Q=Сзак

Интервал (эффективного решения) для которого затраты не превосходят min-е затраты не более чем на 3%. Практически эффективное решение – интервал значений.

Аналогичные задачи возникают:

1. При оптимизации затрат в производственно-транспортных моделях

2. При определении оптимального режима производства и хранения

3. При оптимизации в задачах управления запасами

Балансовые модели.

Модель Леонтьева «затраты – выпуск». Модель Дмитриева «затраты – цены». Балансовые модели предприятий. Балансовая модель вспомогательного производства.

Модель Леонтьева «затраты – выпуск». Межотраслевой баланс обычно строится в виде таблицы, описывающей баланс пр-ва и потр-я внутри страны. Обычно МОБ рассм-ют двух видов: в натуральном и стоимостном выр-ии. Пусть эк-ка страны разделена на n отраслей, каждая из которых яв-ся как потребителем продукции отраслей, так и поставщиком своей. Рассм. МОБ в стоим. выр-ии.

отр-потр. отр- поставщ	1…	n	КП	ВП
1…	х11… I	х1n	у1	x1 II
n	хn1…	хnn	уn	xn
ЗТ труда	V1…	Vn III	V кон
чист. Дох.	m1…	mn	m кон	IV
всего	х1…	хn

Х- ско-ко необходимо отгрузить одной продукции для пр-ва другой. Составили таб. МОБ и выделили 4 квадранта: I-IV. 1. Составим по строкам распред-е валового продукта отрасли поставщика 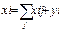(1), где xij-межотраслевой поток м/у отраслью i и j. 2. Составим по столбцам баланс для отрасли потребителя. (2). По столбцам получ-ся известная ф-ла: , где Pj- ст-ть продукции j-той отрасли, Cj- перенесенная ст-ть на продукт из др. отрасли, Vj- необходимый продукт, mj- прибавочный продукт. Величина (х-у) наз-ся производственное потребл-е. Рассм. каждый из квадрантов. I: рассм-ся межотрсалев. потоки продукции и ср-в пр-ва. II: описывает конеч. и валов. продукт. В КП отраж-ся личное потр-е насел-я, бюджетные ассигнования, ЗТ на оборону… т.е. непроизводственная сфера. III хар-ет стр-ру ВП. Суммарный КП: 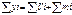. IV хар-ет перераспред-е в эк-ке страны, осуществляемое в кредитно-фин. с-ме. Если МОБ строится на сонлове агрегирования деят-ти предпр-я, то баланс наз-ся отчетным. Для планир-я эк-ки строятся плановые М ОБ. Модель Леонтьева распределения продукции ( «затраты – выпуск»). На основе МОБ построим модель, учитывающую технологические связи м/у отраслями. Для этого вводим коэф-т прямых ЗТ на ед-цу валовой продукции. аij- нормы расходов продукции i-той отрасли по пр-ву ед-цы продукции j-той отрасли. Составим матрицу:

отр-потр. отр- поставщ	Пром-ть	с/х…	прочие	КП	ВП
Пром-ть	a11	a12…	a1n	У1	Х1
с/х…	a21	a22…	a2n	У2…	Х2…
прочие	an1	an2…	ann	уn	хn
Собствен. ЗТ	Z1	Z2…	Zn
Рент-ть	r1	r2…	rn
Цена за ед-цу	p1	p2…	pn

Пусть aij=xij/xj (3), тогда из (1) следует: (4). Введем обознач-я: Х-вектор валовой продукции, У-вектор конечной продукции, А-матрица прямых ЗТ, Е- единичная матрица. Если МРБ задан в натур. ед-х, то матрица А наз-ся технологической; если в стоимостном- то экономической. Из (4): Х=АХ-У или ЕХ=АХ+У, (Е-А)Х=У (5). Обозначим В(n× n)=(Е-А)^-1={b11, bnn}- матрица полных ЗТ на ед-цу конечной продукции. Матричное ур-е Х=ВУ (6). Коэф-ты полных ЗТ м. вычисляться как эл-ты суммы матричного ряда, т.е. (Е-А)^-1=Е+А+А²+А³, здесь А-матрица прямых ЗТ, А²- матрица косвенных ЗТ первого порядка, А³ - второго порядка. Косвенные ЗТ хар-ют ЗТ предшествующих периодов (предшест. труд). Отн-е полных ЗТ к прямым хар-ет КПД эк-ки, т.е. отн-е полных ЗТ с учетом предшествующих к прямым ЗТ: 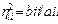. Чем более высокотехнологичней пр-во, тем > знач-е 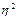. Модель Дмитриева «затраты – цены». Рассм-м модель для опр-я цены продукции. В матрице (по столбцам) опр-ем СБ ед-цы продукции C, Н, для первой продукции: a₁₁p₁+a₂₁p₂++a_n₁p_n+Z₁=C₁, a₁₁p₁+a₂₁p₂++a_n₁p_n=СБ сырья, Z₁-собств. ЗТ. Выразим СБ ч/з рент-ть. Т.к. r1=П1/С1, р1=П1+С1, то р1=r1C1+C1=(r1+1)C1 → С1=p1/(1+r1). Перейдем к матричной записи: (7) {a₁₁p₁+a₂₁p₂++a_n₁p_n+Z₁= p₁/(1+r₁)… a₁_n₁p₁+a₂_np₂++a_nnp_n+Z_n= p_n/(1+r_n). С-ма (7)- с-ма алгебраических ур-й для опр-я равновесных цен, которые удовлетворяют и продавца и покуаптеля при заданной r. При изменении цены в одной отрасли (при тех же остальных условиях) необходимо изменить цены в др. отраслях, чтобы сохранить равновесие цен (7). Рассм-м частный случай нулевой рент-ти r=0: А^т∙ р+Z=p (8), тогда (9) р=(Е-А^т)^-1Z= . -матрица полных ЗТ в модели Дмитриева. Т.о., цены р зависят только от собственных ЗТ Z и технологических способов пр-ва- A^т. Балансовые модели предприятий (для реш-я задач внутризаводского планир-я, выявления резервов, повыш-я эф-ти пр-ва ). Рассм-м ЭММ в матричном виде при реш-и управленческих задач, решаемых на уровне предпр-я. С помощью матричных моделей сопоставляются, балансир-ся и увязываются показ-ли производственно-фин. плана предпр-я. Если в матрич. Модели исп-ся натур. показ-ли, то она наз-ся технологической матрицей, если денежные- экономическая модель. Матрич. Модели рассм-ют осн. показ-ли пр-ва: продукция (осн. и вспом. пр-во), ЗТ, трудовые рес-сы, финансовые показ-ли, товар. и валов. продукция, цены… Осн балансовые соотнош-я модели (по строкам): 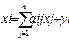, где xi- объем производимой продукции i-того вида, yi- объем конечной, товарной продукции; aij- нормативы потр-я j-той продукции при выпуске i-той продукции. Матричная форма модели сост. из 4 квадрантов:

прод-я пр- ва	прод-я потр-я	цены
квадранты: I, III	квадранты: II, IV
осн прод	всп прод	побоч ЗТ	товар. Прод	валов. прод.
осн пр-во	А (1)	А (2)	-	У (1)	X (1)
вспом пр-во	А (3)	А (4)	-	У (2)	X (2)
вспом ЗТ	-	-	I		II
сырье, матер.	Д (1)	Д (2)			dr
виды оборуд	F (1)	F (2)			fs
виды труда	T (1)	T (2)	III	IV	tg
фин. показ-ли

{осн. пр-во: (1), 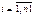; всп. пр-во: (2), } (*). В I квадранте приводятся коэф-ты Aij- норма расходов осн. и всп. пр-ва продукции на пр-во этой же продукции. Они образуют матрицу А, к-я сост. из 4 подматриц А1-А4, учитывающих межцеховые производственные связи: А⁽¹⁾- взаимосвязь м/у пр-вами; А⁽²⁾- нормы потр-я i-той осн. прод-и на выпуск ед-цы j-той прод-и всп. пр-ва; А⁽³⁾- нормы потр-я i-той вспом-ой прод-ии на выпуск ед-цы j-той прод-ии осн-го пр-ва; А⁽⁴⁾- нормы потр-я i-той всп. прод-ии на выпуск ед-цы j-той прод-ии всп. пр-ва. А^(к)={aij⁽^k⁾}, k=1, 2, 3, 4. Во II квадранте отражена конечная прод-я, выходящая за пределы предпр-я, состоящая их двух векторов У⁽¹⁾, У⁽²⁾ осн-го и всп-го пр-ва. Валовый выпуск прод-ии осн-го и всп-го пр-ва: Х⁽¹⁾ и Х⁽²⁾. Т.о. баланс пр-ва и потр-я прод-ии осн-го всп-го пр-ва примет вид с-мы (*). В III квадранте приводятся нормы расх-в сырья, матер., топлива, энергии: Д⁽¹⁾, Д⁽²⁾. Продолжит-ть работы оборуд-я: F⁽¹⁾, F⁽²⁾, нормы времени для трудовых рес-в: Т⁽¹⁾, Т⁽²⁾ на пр-во ед-цы прод-ии осн-го и всп-го пр-ва соот-но. В IV квадранте представлены общие объемы потребляемых рес-в на пр-во прод-ии: dr- матер. рес-сы, fs- время работы обор-я, tg- время работы g-го работника (фонд рабочего времени). Огранич-я: (3) { , , где dr, fs, tg-плановые знач-я пр-ва. Для стоимостной модели таб. пополняется данными побочных ЗТ: цеховые, общезаводские, непроизв.; показ-ли цен, прибыли, финансовые показ-ли. Такая модель основ-ся на исп-ии форм техпромфинплана: плановой калькуляции и смет расх-в. При разработке плана пр-ва предпр-я составляют осн. балансовые ур-я (*), решая их, опр-ют знач-я Х⁽¹⁾, Х⁽²⁾- объемы осн-го и всп-го пр-ва, и и вычисляют потребности в рес-х, исп-я балансовые ур-я (3).

Балансовая модель вспомогательного производства. Наряду с осн-м пр-вом рассм-ют всп. пр-во, вкл-щее ряд цехов. Всп. цеха оказывают услуги как друг другу, так и осн-му пр-ву. Величина ЗТ каждого всп. цеха складыв-ся из собственных ЗТ и ЗТ, связ-х с исп-ем работ др. всп-х цехов. Рассм-м задачу построения баланса пр-ва и распредел-я работ (услуг) всп-х цехов.В этой балансовой модели исп-ся след. обознач-я: Sij- нат. величина, к-я опр-ет кол-во прод-ии/ услуг j-го цеха, поступивших в i-тый цех. Zi, д.е.- собств. ЗТ без ст-ти ЗТ внутризаводского оборота (ст-ти прод-ии, к-я исп-ся внутри предп-я для пр-ва конечного объема ВП). Yi- всего ЗТ i-го цеха. Qj- общий объем прод-ии в натур-х ед-х. Xi-СБ ед-цы прод-ии/ услуг в стоим. или натур. выр-ии. [взаимное представление прод-ии]

83. Производственные функции (ПФ).( Общие представления. Свойства ПФ. Построение ПФ. Методы построения ПФ. )

Общие представления. ПФ в широком смысле наз-ся соотнош-м м/у исп-мыми в пр-ве материальными благами и трудовыми (производственными ) рес-ми и выпущенной прод-ей. Различают: 1. ф-ю выпуска, в к-й в кач-ве независимой переменной берут ЗТ рес-в, а зависимой- выпуск прод-ии. 2. ф-ю производственных ЗТ, в к-й независ. переменная- выпуск прод-ии, ф-я- ЗТ. Произв. рес-сы х: х1, х2… хn. Прод-я у: у1, у2…уm. Тогда ф-я выпуска: y=f(x1, x2…xn) (1); ф-я ЗТ: x=φ (y1, y2…ym) (2). ПФ выр-ют взаимосвязь фактров с рез-ми пр-ва. Их задачей яв-ся исслед-е колич. меры влияния производственных факторов на конеч. рез-т. ПФ примен-ся для анализа, планир-я и прогноз-я на различ-х уровнях упр-я. В кач-ве фактора аргумента х1, х2…хn обычно выступают труд. Рес-сы, ПФ, площади. ПФ м.б.: однофакторной и многофакторной; линейной и нелинейной. Св-ва ПФ. Для простоты будем рассм-ть ПФ с одним продуктом и несколькими рес-ми y=f(x1, x2…xn). Пусть ПФ задана при всех неотриц-х знач-х, яв-ся непрерывной и нужное число раз дифференцируемой (2 р.). Св-ва ПФ: 1) пр-во невозможно при отсут-ии хотя бы одного рес-са (абс-но необходимые рес-сы). 2) при увел-ии ЗТ приозв-х рес-в выпуск прод-ии не снижается: f(x**)≤ f(x*) при х**< х*. Если f(x) дифференцируема, то это предполож-е можно записать в виде: при xj> 0 . Величина - предельная эф-ть. В общем случае пред. эф-ть зависит от х, в к-м она вычисляется. Пред эф-ть хар-ет отн-е прироста выпуска прод-ии к приросту выпуска произв-го рес-са. Мн-во сочетаний рес-в х1…хn, для к-х выпол-ся (2) наз-ся эк-ой областью. Эф-ть исп-я рес-са может также хар-ть сред. эф-ть рес-са f(x)/xi. Эластичность выпуска по отн-ю к изм-ю ЗТ j-го рес-са: 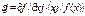показ., на ск-ко % ↑ выпуск у прод-ии при ↑ ЗТ рес-са на 1%. 3) по мере ↑ кол-ва одного ре-са при постоянных кол-вах других пред. эф-ть исп-я этого рес-са не возрастает: 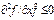. 4) ПФ хар-ся отдачей от расшир-я масштабов пр-ва. Математически зав-ть выпуска прод-ии при пропорц-м измен-ии ЗТ рес-в выр-ся в умножении всех компонент вектора Х на положительный скаляр t. Скалярная ф-я f(x) яв-ся однородной ф-ей степени δ, если она удовлетворяется отн-м: f(tx)=t ^δf(x). Частный случай: 1. если δ > 1, то ПФ хар-ся возрастающей отдачей от расшир-я масштабов пр-ва; 2. если δ =1, постоян. отдача; 3. если δ < 1, убывающая отдача. Очевидно, что δ ≥ 0, иначе не вып-ся св-во 2). Построение ПФ. Постр-е однофакторной ПФ в классе многочленов n-ной степени основана на теореме Ньютона- Лагранжа, в к-й дан способ постр-я ПФ многочлена n-ной степени вида у=а₀+а₁х+а₂х²++а_nxⁿ по (n+1) знач-ю. y₁=f(x₁), y₂=f(x₂)…y_n₊₁=f(x_n₊₁). Коэф-ты а_0… а_n нах-ся из алгебраической суммы ур-й (n+1). Для многофакторных ПФ постр-е основано на опр-ии ее пар-ров, при к-х достигается наилучшее соответствие м/у теоретическими и фактич-ми знач-ми yi. . Обозначим . Строим ПФ при min _i. Эта задача реш-ся неоднозначно. В кач-ве критериев близости часто исп-ся: 1.) min среднего квадрата ошибки. Исп-ся МНК, т.е. или . Алгоритм метода: 1. выбор зависимого показ-ля у и независ-х переменных х. 2. получ-е стат. данных и их первичная обработка. 3. установление мат. формы связи (лин., парабола…). 4. расчет пар-ров а ур-я регрессии из ур-й: . 5. корректировка и эк. интерпретация модели. 6. получ-е эк-х хар-к ПФ. Часто для сущ-я эк. смысла пар-ров ПФ накладыв-ся доп. огранич-я: . 2.) min max-го отклон-я. Для таблицы знач-й xij, где , 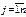(m- № наблюд-я, n- кол-во факторных признаков xj) для многофакторной ф-ии вида рассм-м отлк-я . Пусть max знч-е откл-я =Z, т.е. , тогда получаем ЗЛП: (1) S=Z→ min, (2) {yi-∑ aijxj≤ Z, ∑ aijxj-yi≥ Z, (3) xj, Z≥ 0. Кроме того, этой с-ме м. добавить доп. огран-я на коэф-ты ПФ. 3.) min суммы модулей откл-й. Для случая 2 имеем . (1’) S=∑ Zi→ min, (2’) {yi-∑ aijxj≤ Zi, ∑ aijxj-yi≥ Zi, (3’) xj, Zi≥ 0. Зам. При опр-ии числа эк-х факторов производят их уменьш-е (х1, х2→ к=х2/х1). Эк. анализ ПФ проводится в 3 этапа: 1 обоснов-е выбора ПФ, исходя из их св-в; 2 нах-е коэф-в пФ; 3. анализ пар-ров эк. с-мы на основании ПФ. ПФ яв-ся дескриптивной моделью, и, в частности, м. на основании ее вида решать задачу факторного анализа (инфлюентный анализ).

84. Инфлюентный анализ ЭММ Основные свойства. Методы инфлюентного анализа: точки Лагранжа, цепных подстановок, логарифмирования, эластичности. ПФ в темповой записи.

ИА-сов-ть методов нах-я оценок влияния измен-я факторов на измен-е знач-й результативного показ-ля. Эти знач-я наз-ся инфлюентами. Задачи ИА: 1. опр-ть величину изм-я рез-го показ-ля за счет изм-я каждого из факторов (прямая зад.). 2. опр-ть долю изм-я каждого фактора в общей величине изм-я рез-го показ-ля (обратная зад.). Для ИА необходимо знать зав-ть рез-го показ-ля от фактора, т.е. ПФ: ; все знач-я показ-ля в базисном и отчетном периодах. Выделяют 3 осн. усл-я для метода ИА: 1. приращение рез-го показ-ля ∆ у разлагается без остатка в сумму инфлюент. 2. знач-е каждой инфлюенты опр-ся однозначно и не зав-т от последоват-ти изм-я влияния факторов на прирост рез-го показ-ля. 3. симметричность. Инфлюенты, вычисленные при изм-ии факторов от отчетного периода к базисному, от базисного к отчетному, отлич-ся только знаком. Сущ-ют различные методы ИА. Метод точки Лагранжа. В основе лежит теорема Лагранжа о конеч. приращении ф-ии (для случая нескольких переменных). Теорема. Если ф-я непрерывно дифф-ма на торезке [a, b] по всем переменным, то сущ-ет точка М с координатами (x_i) [a_i, b_i] такая, что f(b₁…b_n)-f(a₁…a_n)= ∑ ( f/ x_i)∆ x_i (=∑ Ux_i). f(b₁…b_n)- знач-е ф-ии на кон. отрезка; f(a₁…a_n)-на начале. С одной стор. ∆ у=∑ Ux_i, с др.- ∆ у= ∑ ( f/ x_i)∆ x_i→ . Т.о. проблема заключ-ся в опр-ии этой точки М. Расс-м параметрическое представление точек отрезка , [0, 1]. Опр-м знач-е 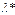, соотв-щее точке М. Для этого представим у как ф-ю от : y=f(x₁…x_n)=F( ), тогда по теор. Лагранжа ∆ F=F(1)-F(0)= . 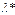Итак, → из этого ур-я нах-м → нах-м полож-е точки М . Алгоритм метода: 1. вычисляем ∆ x_i=х_i⁽¹⁾-x_i⁽⁰⁾, ∆ y=у₁-у₀. 2. записываем параметрическое представление т. М . 3. подставляем это представление в f и нах-м ее как ф-ю от . f(x₁x₂)=F( ). 4. решаем ур-е и нах-м корень 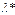[0, 1]. 5. нах-м положение т.М с координатами: . 6. вычисляем инфлюенты (=сила влияния) по ф-ле: , в т.М. Метод цепных подстановок . В этом методы инфлюенты вычисляются по ф-ле: 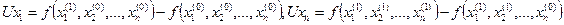. Очевидно, что знач-я инфлюент будут отлич-ся в зав-ти от последоват-ти перемнож-я факторов мультипликативной модели. Т.о. усл-я 1 и 3 вып-ся, а 2 не вып-ся. Рекомендуется порядок рассм-я факторов: а). исходя из усл-й эластич-ти. i₁→ i₂ : 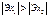б). порядок зависит от значимости факторов (сначала наиболее значимые). в). порядок зав. от способа постр-е ПФ. Метод логарифмиров-я. Применяется для мультипликативной ф-ии вида . Тогда инфлюенты вычисл-ся по ф-ле: . Метод эластич-ти . Исп-ся при небольшой величине ∆ x_i/x_i, менее 50%. → .

ПФ в темповой записи. На ряду с рассм-м объемных показ-лей выпуска и затрат м. установить связи м/д темпами прироста этих показ-лей. Расс-м ПФ Кобба- Дугласа (1). Обозначим темпы прироста этих величин маленькими буквами: для дискретной ф-ии: y=∆ Y(=Y_t₊₁-Y_t)/Y, k=∆ K/K, l=∆ L/L. Для непрерывной ф-ии ч/з производные: y=Y’/Y, k=K’/K, l=L’/L, (‘=d/dt). Логарифмируем (1): и дифф-ем (1): 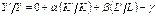, получаем: (2)- ПФ К-Д в темповой записи, где γ - часть темпа прироста у, к-я не связана с приростом затрат капитала К и труда L, т.е.выр-ет интенсификацию пр-ва на макроуровне.

85. Модели календарного планирования.

Теория расписаний. Общая задача календарного планирования. ЭММ оптимального режима производства и хранения.

Модели календарного планирования.

Теория расписаний – с-ма качеств-х и вычислит-х методов, позовляющих упорядочить во времени исп-е с-мы машин для обработки некоторого мн-ва изделий. При этом д.б. удовлетворены опр. технологич. усл-я и обеспечено достиж-е оптим-го знач-я заданного критерия кач-ва расписания. Сферой практич-го прилож-я теор. расписания яв-ся календарное планир-е- область исследов-я операций, в к-й разрабатыв-ся теории и методы оптим-го в смысле упорядоченного во времени конечного мн-ва работ, выполняемых на заданном произв-м оборуд-ии, т.е. производится моделиров-е во времени. Вследствие большого разнообразия производст-х усл-й не сущ-ет универсальной подстановки задачи календарного планир-я. Обычно рассм-ся модель календ-го план-я работы участка единичного или мелкосерийного пр-ва, к-я наз-ся общая задача календ-го план-я. Применительно к машинно-строит. пр-ву расс-ся цех, к-й располагает оборуд-ем m различ-х видов. С помощью этого оборуд-я за плановый период Т в цехе д.б. обработано n видов изделий, кол-во к-х опр-ся планом. В общем случае план выпуска различ-х деталей задается с разбивкой на подпериоды (дни или декады). Известны нормы ЗТ времени на обработку каждого вида деталей на различ-х видах оборуд-я., а так же длит-ти переналадок станков. Известны матрицы движ-я деталей в процессе их обработки. Задача: опр-ть режим работы каждого вида оборуд-я и цеха в целом, при к-м план-график выпуска изделий обеспечен необходимым кол-м деталей при min сумме ЗТ за весь плановый период. Эта задача позволяет опр-ть: 1. оптим. очередность запуска различ-х видов деталей в пр-во. 2 оптим. размер партий деталей в процессе их обработки. 3. оптим. технолог-ие маршруты движ-я деталей в процессе обработки. 4. оптим. режим работы каждого вида оборуд-я. В общем случае это задача мат-го программиров-я: (1) 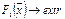, (2) fi( )> < bi, (3) ≥ 0. Если в модель ввести упрощения, то м. сформулировать 4 задачи, одна из к-х след.: для отдельного изделия, потреб-ти в к-м неравномерны во времени, треб-ся опр-ть оптим. режим пр-ва и хранения. При этом min-ся изд-ки, связанные с неравномерностью графика пр-ва и содержанием запасов. ЭММ оптимального режима производства и хранения . Данную задачу будем представлять как модель линейного программир-я. Исходными данными для постр-я модели яв-ся график выпуска готовой прод-ии. Для каждой детали (узла) д.б. известно: - шифры деталей о комплектующих; - кол-во деталей на ед-цу изделий; - срок опережения выпуска деталей цехом по отн-ю к выпуску готовых изделий. Обычно график потреб-ти изделий не совпадает с графиком пр-ва, к-й д.б. равномерным. Концептуальная модель (постановка задачи): для каждого планируемого отрезка времени (декады) известна потр-ть в некоторых деталях. Известен начальный запас детали. Задача: опр-ть выпуск деталей за каждую декаду периода такой, при к-м min-ны как колеб-я графика выпуска, так и остатки незавершенного пр-ва (запас). Обознач-я: n-кол-во декад; t- порядковый № декады, 0≤ t≤ n; at- потреб-ть в деталях в t-той декаде; S0- начальный запас деталей; xt- выпуск деталей на конец t-той декады; St- запас деталей к концу t-той декады. Сотавл-е мат. модели: т.к. S_t-1+x_t=a_t+S_t (a), то x_t+ S_t-1+-S_t= a_t(б). Равномерность выпуска орп-ся разностью (x_t₊₁-x_t). Чем < разность, тем стабильнее график впуска. Эта величина яв-ся знакоперемнной, т.е. ∆ t+1= x_t₊₁-x_t {> 0, прирост выпуска; =0, постоян. выпуск; < 0, уменьш-е выпуска. Т.к. в ЗЛП переменные б.д. ≥ 0, то представим ∆ t+1 в виде разности неотриц-х величин, т.е. x_t₊₁-x_t= Y_t-Z_t; Yt, Zt≥ 0. Yt- прирост выпуска прод-ии, Zt- сниж-е выпуска прод-ии при переходе от t к t+1. Переносим перемнные в левую часть: x_t₊₁-x_t-Y_t+Z_t=0. Т.к. в целевой ф-ии д.б. отражена колеб-ть выпуска прод-ии Yt и остатки незавершенного пр-ва- запас St, то ЗЛП имеет вид: (1) L=∑ Y_t +∑ S_t → min, (2) { x_t₊ S_t_-1+-S_t= a_t, x_t₊₁-x_t-Y_t+Z_t=0; (3) x_t, Y_t, Z_t, S_t≥ 0. Зам. В ЗЛП в целевой ф-ии (1) приоритеты колеб-ти графика выпуска и увелич-я запасов одинаковы. При реш-ии конкретной задачи рассм-ся 2 ситуации: 1. приоритет роста запасов выше (Н, производ. и складские площади ограничены), то целев. ф-я L₂=∑ Y_t +р∑ S_t → min, р> 1 (р- некоторое число). 2. приоритет равномерности выпуска выше, тогда целев. ф-я я L₃=q∑ Y_t +∑ S_t → min, q> 1(q- некоторое число). Коэф-ты q, p подбираются для каждого пр-ва конкретно. Их выбор м. осущ-ть методом ЭО.

86 Сетевые транспортные модели.

Сущ-ет ряд задач, к-е удобно представить в виде графич-х стр-р, Н, графически м. формализовать процесс принятия реш-й (дерево реш-й), функционир-е произвд-й с-мы, транспортировку прод-ии. т.д. Для постр-я и исслед-я граф-х стр-р разработана с-ма методов, изучаемая в теории графов. Рассм-м осн. понятия теории графов и ее примен-е к реш-ю задачи постр-я max-го потока трансп-х сетей. Пусть задана непустое мн-во Х с эл-ми xi и мн-во U, состоящее из пар эл-в {xi, xj} X. X и U задют граф G(X, U). Эл-ты мн-ва Х- вершины графа, эл-ты U-ребра Если эл-ты в парах мн-ва U упорядочены, то G наз-ют ориентированным графом. Иначе - неориентированным. А эл-ты мн-ва наз-ют дугами. Граф-ки граф задается в виде точек и линий, их соединяющих. Ребро, нач. и конец к-го совпадают, -петля. Вершины наз-ся смежными, если сущ-ет соединяющее их ребро. Если вершина яв-ся началом или концом ребра, то верш. и ребро наз-ся инцидентными. Степенью вершины наз-ся число индентных ей ребер: d{xi}. Вершина, степнь к-й =0, наз-ся изолированной; =1, то тупиковой. Маршрут в графе- последоват-ть вершин и ребер, в к-й конец предыдущего ребра совпадает с началом следующего (кроме первого и последнего ребра). Длина маршрута- число ребер, входящих в маршрут. Цепь- маршрут, в к-й все ребра попарно различны. Простой наз-ся цепь, где вершины попарно различны. Цикл- цепь, в к-й нач. и кон. совпадают. Граф наз-ся связным, если для любых двух его вершин сущ-ет цепь, соед-щая эти вершины. Расстояние м/у вершинами связного графа- длина самой короткой цепи, соед-щей вершины. Диаметр графа- max-ое расстояние м/у вершинами. Дерево- связный граф без цикла. Граф наз-ся полным, если любые 2 его вершины соединены ребром. Граф наз-ся регулярным степени d, если все его вершины имеют степень d. В ориентированном графе все дуги имеют направл-я, указанные стрелкой. Маршрут в ориент-м графе часто наз-ют контуром. Полустепенью исхода вершины Х наз-ся число дуг, исходящих из этой вершины. Полустепенью захода наз-ся число дуг, заходящих в эту вершину. Транспортные сети . Опр1. Двухполюсной трансп-ой сетью S наз-ся произвольный ориентиров. граф без петель, с мн-вом вершин Х и дуг U, для к-х вып-ся усл-я: 1. сущ-ет единственная вершина S X, в к-ю не заходит ни одна дуга u U. Эта вершина S наз-ся источником/ входом сети. 2. сущ-ет единств. вершина t X, из к-й не выходит ни одной дуги u U. Вершина t наз-ся стоком/ выходом сети. 3. на мн-ве дуг U сети S опр-на неотриц-ая ф-я С (R⁺ {0}), ставящая в соответствие каждой дуге u U неотриц-ое вещественное число C(U), называемое пропускноу способностью дуги U. Опр2. Потоком в сети S от выхода s X к выходу t X (из ист-ка S в сток t) наз-ся произвольная неотриц. вещественная ф-я, опр-мая на мн-ве дуг сети φ, для к-й вып-ся усл-я: 1. 0≤ φ (U)≤ C(U): поток по каждой дуге≤ ее пропускной способ-ти, 2. для любого х X, кроме x=S, x=t. 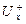Мн-во - мн-во дуг, заходящих в вершину Х; - выходящих из Х: кол-во потока, входящего в вершину, = кол-ву потоков, исходящих из нее (кроме входа и выхода сети). Т.о. кол-во потока выходящего исхода = кол-ву входящего и наз-ся величиной потока φ _s. Опр3. 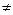Разрез цепи S (P(A)), заданной на мн-ве вершин А Х (А 0, А 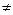Х), это мн-во дуг {xi, xj} Uдуг таких, что xi A, xj{xi, xj} (X-A). При чем вход S A, а выход t (X-A). Опр4. Пропускная способности (величина разреза) наз-ся сумма пропускных способ-тей входящих в него дуг: C(A)=∑ C(U), когда U P(A). Теоремы о транспортных потоках . Т1. Если S А, t (X-A), то величина любого потока У, проходящего из ист-ка S в сток t, опр-ся по ф-ле: φ _s=φ (А, Х-А)-φ (Х-А, А). Т.о. величина потока в сети измер-ся ч/з разность знач-й потока, ч/з разрез и знач-е потока, идущего в обратном направл-ии. Min-ым разрезом, разделяющим вход S и выход t сети наз-ся произвольный разрез Р(А), S A, t (X-A) с minпропускной способностью. Т2. Величина любого птока от входа к выходу не превосходит пропускной способности min-го разреза, разделяющего вход и выход сети. При чем сущ-ет max-ый поток, чья величина = пропускной способ-ти min-го разреза. Опр5. Дуга u U, соед-щая вершины xi, xj из Х сети S яв-ся допустимой дугой, если для нее вып-ся одно из усл-й: 1. если направл-е дуги совпадает с напр-м потока, и знач-е потока по этой дуге < ее пропускной способ-ти, т.е. U(xi, xj): φ (U)< C(U). 2. напр-е дуги противоположно напр-ю потока, и по ней проходит нулевой поток. U(xi, xj): φ (U)> 0. Дуги, для к-х вып-ся усл-е1, наз-ся увеличивающимися, а усл-е 2- уменьшающимися. Опр6. Увеличивающейся цепью, соед-щей вход и выход сети, наз-ся цепь, все дуги к-й яв-ся допустимыми. δ =min(∆ (U)); ∆ U={ C(U)- φ (U), U↑; φ (U), U↓. По каждой увел-щейся дуге поток м. ↑ на δ, по уменьш-щейся- ↓ на δ. Алгоритм постр-я max-го потока . 1. задаем начальное знач-е потока (обычно 0). 2. строим увеличивающуюся цепь от S к t. Если такой цепи не сущ-ет, то max-ый поток построен, и его знач-е = φ _s_.3. вдоль построенной цепи увел-ем знач-е потока на δ и переходим к щагу 2. По всем дугам, заходящим в t, поток равен их пропускным способностям. Такие дуги наз-ся насыщенными. Док-м того, что построенный поток max, будет указание разреза, величина к-го = знач-ю построенного потока. При моделиров-ии реальных задач м. исп-ся с неориентированными дугами. В этом случае предостав-ся доп. возм-ти при выборе оптим-го реш-я. Н, если на уч-ке обраб-ся детали с незаданным жестко порядком вып-я операции, то, изменяя направл-я их перемещ-я м/у станками, м. увеличить пропускную способность уч-ка. Т.к. по неориентированному ребру ток м. идти в любом напр-ии, то следует каждое ребро заменить двумя противоположно направленными дугами с той же пропускной способностью. Максимальный поток нах-ся по изложенному выше алгоритму. В общем случае для неориентированной сети max поток ≥, чем для ориентир. сети с той же стр-рой. Трансп. сеть вместе с проходящим по ней потоком м. ипс-ть, Н, для моделир-я передачи инф-ии в комп. сети: источник- фирма, генерирующая инф-ю. Вершина сети- пользователи, не имеющие права изменять ее. Сток- глав. польз-ль, к-му разрешено не только считывать, но и работать с полученной инф-ей.

Модели управления запасами.

⇐ Предыдущая 37 38 39 40 414243 44 45 46 Следующая ⇒