Собственные векторы и собственные значения матриц

1. Пусть 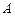– квадратная матрица порядка 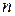и . Число называется собственным значением матрицы , если существует ненулевой вектор 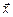, такой что выполнено равенство

Вектор 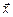, удовлетворяющий данному соотношению называется собственным вектором матрицы , соответствующим собственному значению .

Справедливы следующие свойства.

1. Собственному вектору матрицы соответствует единственное собственное значение. Действительно, если – два собственных значения вектора , то и , откуда или , значит 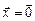, что противоречит определению. Значит .

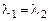2. Если 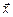собственный вектор матрицы 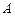, удовлетворяющий собственному значению , и – произвольное действительное число, то - так же собственный вектор с собственным значением . Действительно, умножим обе части равенства на , получим или , следовательно, ненулевой вектор , удовлетворяет определению и поэтому является собственным вектором матрицы , соответствующим собственному значению .

3. Если и линейно независимые собственные векторы матрицы с одним и тем же собственным значением , то + – собственный вектор с собственным значением . Действительно, в силу линейной независимости и , причём , что согласно определению и означает, что вектор – собственный, отвечающий собственному значению .

4. Собственные векторы матрицы , соответствующие попарно различным собственным значениям являются линейно независимыми. Докажем свойство для . Пусть и , . Предположим, что и - линейно зависимы, следовательно, существует линейная комбинация причём хотя бы один из коэффициентов и 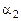ненулевой. Пусть , тогда где . Значит, согласно свойству 2 вектор является собственным вектором матрицы , отвечающим собственному значению 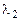. Из единственности собственного значения для вектора следует, что 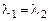. Значит, векторы и линейно независимы.

Преобразуем равенство

получим

В развёрнутом виде данное равенство есть однородная система уравнений с неизвестными. Такая система имеет ненулевое решение тогда и только тогда, когда её определитель равен нулю, то есть

Левая часть есть многочлен степени по . Он называется характеристическим многочленом матрицы . Данное уравнение называется характеристическим уравнением, а его корни – характеристические числа или собственные значения матрицы . Совокупность всех собственных значений матрицы с учётом их кратности (как корней характеристического уравнения) называется спектром матрицы .
2. Приведение матрицы к диагональному виду
ТЕОРЕМА 1. Сумма собственных значение матрицы А, равна сумме её диагональных элементов, а произведение собственных значений равно определителю матрицы.

Рассмотрим случай размерности . Выпишем характеристическое уравнение:

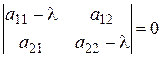или .

По теореме Виета, 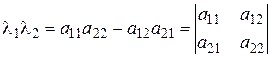и .

Если матрица А имеет треугольный или диагональный вид, то собственные значения в точности совпадают с диагональными элементами. Поставим задачу привести данную матрицу к диагональной или треугольной форме не меняя собственных значений.

Квадратная матрица А называется приводимой к диагональному виду, если существует невырожденная матрица такая, что – диагональная.

ТЕОРЕМА 2. Пусть А – квадратная матрица порядка имеет линейно независимых собственных векторов. Если взять эти векторы в качестве столбцов матрицы , тогда матрица имеет диагональный вид, причём на диагонали стоят собственные значения матрицы А, то есть

Пример

Пусть дана леонтьевская балансовая модель «затраты–выпуск». Определить, будет ли продуктивной матрица технологических коэффициентов . Найти вектор валовой продукции при заданном , где

; .

► Для решения вопроса о продуктивности матрицы следует найти собственные значения этой матрицы. Составим характеристическое уравнение:

или

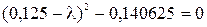Следовательно, ; . Оба корня по модулю меньше единицы, значит, матрица технологических коэффициентов продуктивная. Для определения вектора валовой продукции имеем формулу . Найдем обратную матрицу для матрицы

Обозначим , тогда . Следовательно,

.◄

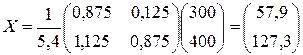Пример (простая модель обмена)

Пусть имеется система 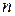отраслей производства , каждая из которых выпускает продукцию одного вида. Примем за единицу объем продукции каждой отрасли в рассматриваемом периоде. Обозначим через 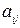долю продукции отрасли , которая поступает в отрасль . Будем считать, что обмен продукцией происходит только внутри системы (система замкнута), т.е. . Рассмотрим матрицу коэффициентов :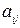

где .

Матрица со свойством (сумма элементов ее любого столбца равна единице), называется матрицей обмена. Требуется установить такие цены на продукцию каждой отрасли, при которых вся система находится в равновесии, т.е. ни одна отрасль не обогащается за счет другой.

Пусть - цена одной единицы продукции отрасли , а - вектор цен. Тогда расход отрасли , т.е. стоимость всей закупаемой ее продукции определяется как

Чтобы отрасль могла развиваться, ее расход не должен превышать дохода, который равен стоимости произведенной ее продукции, т.е. :

Если искомые равновесные цены существуют, то система данных неравенств выполняется для них как система равенств:

Данную систему удобно записать в матричном форме

или .

Матричное уравнение означает, что собственный вектор матрицы обмена , отвечающий ее собственному значению , представляет собой искомый вектор равновесных цен.

Пример (модель международной торговли)

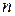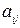Пусть имеется система стран , бюджет каждой из которых равен соответственно . Обозначим через долю бюджета , которую страна тратит на закупку у страны . Будем считать, что весь бюджет расходуется на закупку товаров либо внутри страны, либо на импорт из других стран (система замкнута), т.е. .

Рассмотрим матрицу коэффициентов :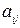

где .

Матрица со свойством (сумма элементов ее любого столбца равна единице), называется структурной матрицей торговли.

Требуется найти вектор бюджетов стран , обеспечивающий равновесие всей системы, при котором отсутствует значительный дефицит торгового баланса для каждой из стран участниц.

Для любой страны , выручка от внешней и внутренней торговли определяется как .

Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е.

Если искомые бездефицитные бюджеты существуют, то данная система неравенств выполняется для них как система уравнений:

Данную систему можно записать в матричной форме:

или .

Матричное уравнение означает, что собственный вектор структурной матрицы торговли , отвечающей ее собственному значению , состоит из бюджетов стран бездефицитной международной торговли.

Пример

Экономическая система состоит из трех отраслей производства, каждая из которых выпускает один вид продукции. Обмен внутри системы происходит в соответствии с данной матрицей обмена

Найдите вектор равновесных цен.

► Найдем собственный вектор , матрицы , отвечающий ее собственному значению , решив уравнение , которое в нашем случае имеет вид

Решив ее, найдем . Полагая , находим равновесные цены на продукцию каждой отрасли: , где параметр можно трактовать как множитель, связанный с денежной единицей. ◄

Пример

Структурная матрица торговли трех стран имеет вид

Найдите соотношение бюджетов этих стран для сбалансированной торговли.

Решив данную однородную систему линейных уравнений, получим . Полученный результат означает, что при бюджеты стран определяются как 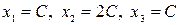, и сбалансированность торговли трех стран достигается при следующем соотношении бюджетов .◄

Пример

Структурная матрица торговли четырех стран имеет вид

Найдите бюджеты этих стран, удовлетворяющие сбалансированной торговли при условии, сумма бюджетов задана:

(усл. ден. ед.)

Решив данную систему получим 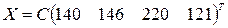. Полученный результат означает, что при бюджеты стран определяются как . Подставив найденные значения в заданную систему бюджетов, получим , откуда . Окончательно находим искомые величины стран при бездефицитной торговле (в усл. ден. ед.): ◄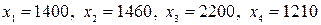

§6. Квадратичные формы и их применения

1. Квадратичной формой 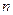переменных 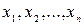, принимающих числовые значения, называется числовая функция вида

где - числа, называемые коэффициентами квадратичной формы.

Матрицей квадратичной формы 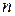переменных 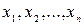, называется симметрическая матрица порядка 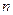, элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в ой строке ом столбце, равен половине коэффициента при в квадратичной форме.

Рангом квадратичной формы называется ранг её матрицы. Квадратичная форма может быть записана в матричном виде где матрица квадратичной формы и .

Квадратичная форма называется канонической (имеет канонический вид), если коэффициенты при , то есть, если матрица квадратичной формы диагональная и следовательно

где не все коэффициенты равны нулю.

ТЕОРЕМА (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.

Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны .

Квадратичная форма называется положительно (отрицательно) определённой, если при всех и положительно (отрицательно) полуопределённой, если при всех .

ТЕОРЕМА (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны, то есть, чтобы

Здесь -угловые миноры матрицы квадратичной формы.

Следствие

Для того чтобы квадратичная форма была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались следующим образом:

Типовые примеры

1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование

► Следуя алгоритму метода Лагранжа, выделим вначале в квадратичной форме все члены, содержащие , и дополним их до полного квадрата:

Сделаем в этом выражении замену и подставим его в квадратичную форму. Получим:

Далее выделим в члены, содержащие и проделаем с ними аналогичную процедуру:

Если положить 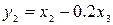, то квадратичная форма уже не будет содержать смешанных произведений. Примем также 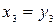, тогда

канонический вид квадратичной формы есть

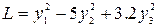Соответствующее преобразование от переменных 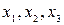к переменным имеет вид:

.◄

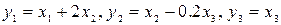2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:

► В исходном базисе 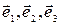матрица оператора, соответствующая данной квадратичной форме, есть

Эта матрица будет определять квадратичную форму канонического вида в ортонормированном базисе , составленном из собственных векторов матрицы . Найдем их. Характеристическое уравнение для матрицы имеет вид

Откуда следует

и .

Как известно собственные векторы матрицы находятся из уравнений

Для случая имеем:

Ранг матрицы этой системы уравнений (относительно ) равен 1. Следовательно, ФСР системы состоит из двух линейно независимых решений.

Как видно из данной системы, величина принимает произвольные значения, а величины связаны соотношением . В качестве собственных можно выбрать, например, векторы

Эти векторы ортогональны: (если бы они оказались не ортогональными, то их нужно было бы ортогонализировать с помощью стандартной процедуры). Вектор к тому же и нормирован. Откуда следует - . Нормируем теперь вектор :

Для случая уравнение, определяющее собственный вектор есть

Ранг матрицы этой системы уравнений равен 2. Следовательно она имеет одно линейно независимое решение, например, Отнормируем этот вектор: .

Теперь можно составить искомую матрицу ортогонального преобразования:

Исходная квадратичная форма будет иметь следующий канонический вид

При этом переменные связаны с переменными соотношением

или

.◄

3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду

► Выделим в этом выражении квадратичную форму . Это три первых слагаемых уравнения .

Матрица квадратичной формы равна . Проведём процедуру приведения квадратичной формы к каноническому виду с помощью ортогонального преобразования. Характеристическое уравнение матрицы имеет вид

Его корни таковы: . Найдём теперь собственные векторы, соответствующие этим корням и ортонормируем их. Для вектора 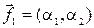, соответствующего 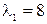, имеем

В итоге собственный вектор, соответствующий 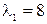, можно выбрать в виде

Аналогичная процедура для собственного вектора даёт:

Откуда:

После нормировки полученных векторов имеем:

Эти векторы представляют собой ортонормированный базис новой системы координат. Матрица ортогонального оператора, приводящего квадратичную форму 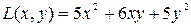к каноническому виду , есть

Связь старых и новых координат определяется соотношением .

Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду

. Это есть каноническое уравнение эллипса в системе координат , которая получается из исходной её поворотом на угол и переносом начала координат в точку .◄

Предыдущая 1 2 3 4 5 6 7 89Следующая