Изучение сезонных колебаний в динамическом ряду
Расчёт индексов сезонности
Динамические ряды, состоящие из месячных или квартальных уровней обычно содержат периодические колебания, связанные со сменой времён года, и называются сезонными.
Для выявления интенсивности сезонных колебаний применяют различные способы расчёта индексов сезонности:
1) метод простых средних;
2) метод помесячных отношений;
3) метод скользящих средних.
Метод простых средних состоит в определении простой средней за одни и те же месяцы всего изучаемого периода, а затем в сопоставлении полученных средних со средней за весь изучаемый период.
Например: Имеются данные о механическом движении населения в Хабаровском крае (таблица 26):
Решение
Таблица 26 − Расчётная таблица
| Месяц
| Сальдо миграции, чел.
| Сальдо миграции в среднем за 3 года
| Индексы сезонности, %
| |
|
|
| | январь
| -17, 0
| -186, 0
| -153, 0
| -118, 7
|
| | февраль
| -57, 0
| 71, 0
| -110, 0
| -32, 0
|
| | март
| 69, 0
| -5, 0
| 71, 0
| 45, 0
| -90
| | апрель
| 263, 0
| 189, 0
| -463, 0
| -3, 7
|
| | май
| 112, 0
| 13, 0
| -150, 0
| -8, 3
|
| | июнь
| 358, 0
| -34, 0
| -301, 0
| 7, 7
| -10
| | июль
| -88, 0
| -91, 0
| -379, 0
| -186, 0
|
| | август
| -182, 0
| -181, 0
| -358, 0
| -240, 3
|
| | сентябрь
| 174, 0
| 14, 0
| -193, 0
| -1, 7
| 3, 2
| | октябрь
| -179, 0
| -93, 0
| -170, 0
| -147, 3
|
| | ноябрь
| 164, 0
| -61, 0
| -219, 0
| -38, 7
|
| | декабрь
| 89, 0
| 416, 0
| -219, 0
| 95, 3
| -180
| 1. Определяем среднемесячный уровень сальдо миграции за 3 года:
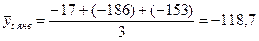 ; ;
 и т.д. и т.д.
2. Вычисляем среднюю из среднемесячных уровней:
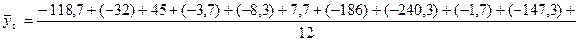  . .
3. Находим индексы сезонности:
 ; ;
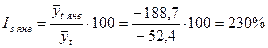 ; ;  и т.д. (таблица 26). и т.д. (таблица 26).
4. Изобразим сезонную волну на графике (рисунок 4):

Рисунок 4 – Сезонная волна сальдо миграции в Хабаровском крае
Метод помесячных отношений заключается в том, что вычисляется по каждому году цепные темпы роста месячных уровней, а затем из полученных отношений определяется средняя арифметическая.
Например: По данным предыдущего примера (таблица 26) рассчитаем индексы сезонности методом помесячных отношений:
Решение
Таблица 27 − Расчётная таблица
| Месяц
| Помесячные отношения, %
| Средняя помесячных отношений, %
| |
|
|
| | январь
| -
| -209, 0
| -36, 8
| -122, 9
| | февраль
| 335, 3
| -38, 2
| 71, 9
| 123, 0
| | март
| -121, 1
| -7, 0
| -64, 5
| -64, 2
| | апрель
| 381, 2
| -3780, 0
| -652, 1
| -1350, 3
| | май
| 42, 6
| 6, 9
| 32, 4
| 27, 3
| | июнь
| 319, 6
| -261, 5
| 200, 7
| 86, 3
| | июль
| -24, 6
| 267, 6
| 125, 9
| 123, 0
| | август
| 206, 8
| 198, 9
| 94, 5
| 166, 7
| | сентябрь
| -95, 6
| -7, 7
| 53, 9
| -16, 5
| | октябрь
| -102, 9
| -664, 3
| 88, 1
| -226, 4
| | ноябрь
| -91, 6
| 65, 6
| 128, 8
| 34, 3
| | декабрь
| 54, 3
| -682, 0
| | -313, 8
|
1. Найдем цепные темпы роста:
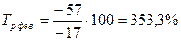 ; ;  и т.д. и т.д.
2. Рассчитаем их среднюю арифметическую:
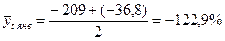 ; ; 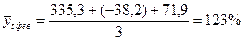 и т.д. (таблица 27). и т.д. (таблица 27).
Метод подвижных или скользящих средних. Главный уровень определяется путём вычисления 12-ти месячных скользящих средних.
Например: Воспользуемся данными о механическом движении населения в Хабаровском крае (таблица 26).
Решение
1. Расчёт 12-членной скользящей средней проведем по формуле средней хронологической:
 ; ;
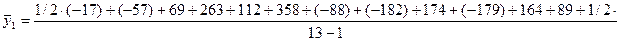 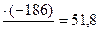 ; ;
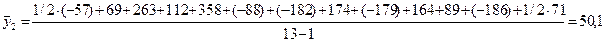 и т. д. и т. д.
Таблица 28 − Расчётная таблица
| Месяц
| 12-членная скользящая средняя
| Индекс колеблемости, %
| Индексы сезонности, %
| |
|
|
|
|
|
| | январь
| -
| 2, 0
| -123, 2
| -
| -9110, 2
| 147, 4
| -4481, 4
| | февраль
| -
| -4, 7
| -139, 2
| -
| 3625, 5
| 89, 3
| 1857, 4
| | март
| -
| -7, 8
| -151, 0
| -
| 107, 1
| -51, 0
| 28, 1
| | апрель
| -
| -13, 5
| -160, 8
| -
| -2438, 7
| 306, 5
| -1066, 1
| | май
| -
| -9, 3
| -193, 9
| -
| -96, 0
| 93, 3
| -1, 4
| | июнь
| -
| 5, 7
| -214, 0
| -
| 365, 9
| 155, 3
| 260, 6
| | июль
| 51, 8
| -0, 5
| -
| -169, 9
| -1594, 2
| 177, 1
| -708, 5
| | август
| 50, 1
| -4, 8
| -
| -363, 4
| 39490, 9
| -
| -882, 0
| | сентябрь
| 52, 3
| -28, 8
| -
| 332, 5
| -289, 7
| -
| 19563, 8
| | октябрь
| 46, 2
| -62, 8
| -
| -387, 7
| 322, 5
| -
| 21, 4
| | ноябрь
| 39, 0
| -80, 7
| -
| 421, 0
| 97, 1
| -
| -32, 6
| | декабрь
| 18, 5
| -103, 8
| -
| 481, 1
| -515, 4
| -
| 259, 1
| 2. Рассчитаем индекс колеблемости по формуле 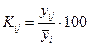 , ,
где  − номер месяца; − номер месяца;
 − номер года. − номер года.
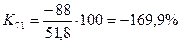 ; ; 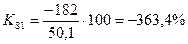 и т.д. и т.д.
3. Рассчитаем индекс сезонности по формуле 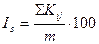 , ,
где  − число индексов колеблемости за месяц. − число индексов колеблемости за месяц.
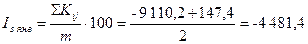 ; ;  и т.д. (таблица 28). и т.д. (таблица 28).
Модели периодических колебаний
Построение модели сезонной волны позволяет изучать размах сезонных колебаний. Модель периодических колебаний хорошо описывает ряд Фурье:
 , ,
где 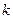 − определяет номер гармоники ряда Фурье (обычно от 1 до 4). − определяет номер гармоники ряда Фурье (обычно от 1 до 4).
При решении уравнения параметры определяются на основе положений метода наименьших квадратов.
Для вычисления параметров уравнения ряда Фурье используют следующие формулы:
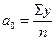 ; ; 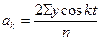 ; ;  . .
Последовательные значения 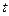 (времени) выражаются в радиальной мере или в градусах и определяются от 0 с увеличением (приростом), равным (времени) выражаются в радиальной мере или в градусах и определяются от 0 с увеличением (приростом), равным 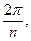
где 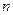 − число уровней эмпирического ряда. − число уровней эмпирического ряда.
Для изучения сезонности используют 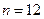 (по числу месяцев в году) или (по числу месяцев в году) или 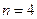 (по числу кварталов в году). (по числу кварталов в году).
При 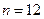 значения представлены в таблице 29. значения представлены в таблице 29.
Таблица 29 − Значения синусов и косинусов 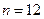 , при , при  
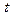
| 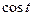
| 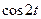
| 
| 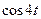
| 
| 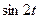
| 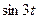
| 
| |
|
|
|
|
|
|
|
|
| 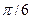
| 0, 866
| 0, 5
|
| -0, 5
| 0, 5
| 0, 866
|
| 0, 866
| 
| 0, 5
| -0, 5
| -1
| -0, 5
| 0, 866
| 0, 866
|
| -0, 866
| 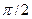
|
| -1
|
|
|
|
| -1
|
| 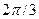
| -0, 5
| -0, 5
|
| -0, 5
| 0, 866
| -0, 866
|
| 0, 866
| 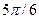
| -0, 866
| 0, 5
|
| -0, 5
| 0, 5
| -0, 866
|
| -0, 866
| 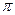
| -1
|
| -1
|
|
|
|
|
| 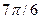
| -0, 866
| 0, 5
|
| -0, 5
| -0, 5
| 0, 866
| -1
| 0, 866
| 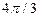
| -0, 5
| -0, 5
|
| -0, 5
| -0, 866
| 0, 866
|
| -0, 866
| 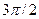
|
| -1
|
|
| -1
|
|
|
| 
| 0, 5
| -0, 5
| -1
| -0, 5
| -0, 866
| -0, 866
|
| 0, 866
| 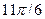
| 0, 866
| 0, 5
|
| -0, 5
| -0, 5
| -0, 866
| -1
| -0, 866
|
На практике при выравнивании ряда Фурье обычно рассчитывают не более 4 гармоник, а затем определяют гармонику, которая наилучшим образом описывает периодичность изменений уровней динамического ряда.
Так при  : :  ; ;
 : :  ; ;
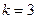 : : 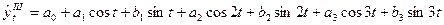 ; ;
 : : 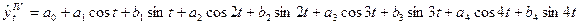 . .
Остаточные дисперсии 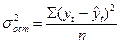 , рассчитанные по каждой из четырёх гармоник, позволяют сделать вывод, какая гармоника Фурье лучше описывает периодичность изменений в исследуемом временном ряду. , рассчитанные по каждой из четырёх гармоник, позволяют сделать вывод, какая гармоника Фурье лучше описывает периодичность изменений в исследуемом временном ряду.
Например: По данным о механическом движении населения в Хабаровском крае (таблица 26) определить модель сезонной волны, рассчитав четыре гармоники ряда Фурье.
Решение
1. Рассчитаем показатели, необходимые для получения уравнения по первой гармонике (таблица 29):
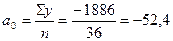 ; ; 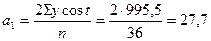 ; ;
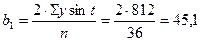 . .
Отсюда уравнение первой гармоники  имеет вид: имеет вид:
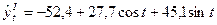
2. Определим теоретические значения первой гармоники:
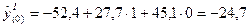 ; ;
 ; ;
 и т.д. (таблица 30). и т.д. (таблица 30).
3. Рассчитаем уравнение второй гармоники  . .
Находим параметры  и и  : :  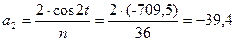 ; ;
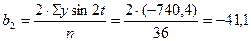 ; ;
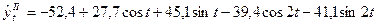 . .
4. Определим теоретические значения второй гармоники:
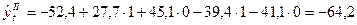
 и т.д. (таблица 30). и т.д. (таблица 30).
5. Рассчитаем уравнение третьей гармоники: 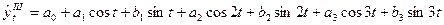 : :
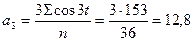 ; ; 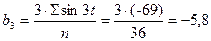 ; ;
 . .
6. Найдём теоретические значения третьей гармоники:
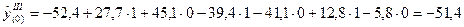 ; ;
 и т.д. (таблица 30). и т.д. (таблица 30).
7. Определим уравнение четвёртой гармоники
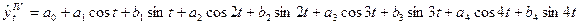 ; ;
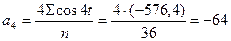 ; ; 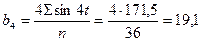 ; ;
  . .
8. Рассчитаем теоретические значения четвёртой гармоники:
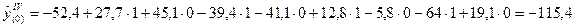 ; ;
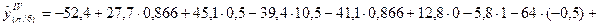 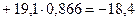 и т.д. (таблица 30). и т.д. (таблица 30).
9. Сальдо миграции наилучшим образом описывается уравнением параболы второго порядка вида  . .
10. Рассчитаем вклад в дисперсию каждой гармоники (таблица 31).
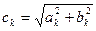 ; ;
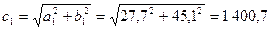 ; ;
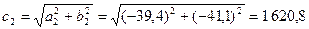 и т.д. и т.д.
Вклад в дисперсию определяется по формуле:  и т.д. (таблица 31). и т.д. (таблица 31).
Вклад отдельный определяется:
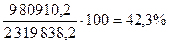 ; ; 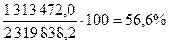 (таблица 31) (таблица 31)
Таблица 30 − Расчётные данные для определения четырёх гармоник Фурье
| Месяц
| Сальдо мигра-ции,
чел. 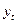
| 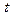
| 
| 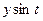
| 
| 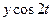
| 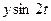
| 
| 
| 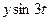
| 
| 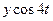
| 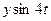
|  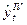
| | |
|
-17, 0
|
|
-17
|
|
-24, 7
|
-17
|
|
-64, 2
|
-17
|
|
-51, 4
|
-17
|
|
-115, 4
| | январь
| | февраль
| -57, 0
| 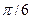
| -49, 4
| -28, 5
| -5, 3
| -28, 5
| -49, 4
| -61, 2
|
| -57
| -67, 0
| 24, 7
| -42, 7
| -18, 4
| | март
| 69, 0
| 
| 34, 5
| 59, 8
| 1, 4
| -34, 5
| 59, 8
| -15, 4
| -69
|
| -28, 2
| -17, 3
| -29, 9
| -12, 6
| | апрель
| 263, 0
| 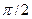
|
|
| -7, 3
| -263
|
| 32, 1
|
| -263
| 37, 9
| 0, 0
| 0, 0
| -26, 2
| | май
| 112, 0
| 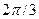
| -56
| 97, 0
| -27, 1
| -56
| -97, 0
| 28, 2
|
|
| 40, 9
| 28, 0
| -48, 5
| 89, 5
| | июнь
| 358, 0
| 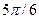
| -310, 0
|
| -53, 8
|
| -310, 0
| -37, 9
|
|
| -43, 6
| 155, 0
| 268, 5
| -28, 1
| | июль
| -88, 0
| 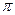
|
|
| -80, 0
| -88
|
| -119, 5
|
|
| -132, 2
| 88, 0
| 0, 0
| -196, 3
| | август
| -182, 0
| 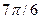
| 157, 6
|
| -98, 9
| -91
| -157, 6
| -154, 2
|
|
| -148, 5
| -78, 8
| 136, 5
| -100, 0
| | сентябрь
| 174, 0
| 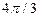
| -87
| -150, 7
| -105, 3
| -87
| 150, 7
| -121, 2
|
|
| -108, 4
| 43, 5
| 75, 3
| -92, 9
| | октябрь
| -179, 0
| 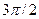
|
|
| -97, 5
|
|
| -58, 1
|
| -179
| -63, 8
| 0, 0
| 0, 0
| -127, 9
| | ноябрь
| 164, 0
| 
|
| -142, 0
| -77, 6
| -82
| -142, 0
| -22, 3
| -164
|
| -35, 0
| -41, 0
| 71, 0
| 13, 5
| | декабрь
| 89, 0
| 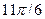
| 77, 1
| -44, 5
| -51, 0
| 44, 5
| -77, 1
| -35, 1
|
| -89
| -29, 3
| -38, 5
| -66, 7
| -13, 8
| |
|
-186, 0
|
|
-186
|
|
-24, 7
|
-186
|
|
-64, 2
|
-186
|
|
-51, 4
|
-186
|
|
-652, 7
| | январь
| | февраль
| 71, 0
| 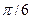
| 61, 5
| 35, 5
| -5, 9
| 35, 5
| 61, 5
| -61, 2
|
|
| -67, 0
| -35, 5
| 53, 2
| -18, 4
| | март
| -5, 0
| 
| -2, 5
| -4, 3
| 0, 5
| 2, 5
| -4, 3
| -15, 4
|
|
| -28, 2
| 2, 5
| 2, 2
| -12, 6
| | апрель
| 189, 0
| 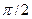
|
|
| -7, 3
| -189
|
| 32, 1
|
| -189
| 37, 9
|
| 0, 0
| -26, 2
| | май
| 13, 0
| 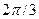
| -6, 5
| 11, 3
| -27, 1
| -6, 5
| -11, 3
| 28, 2
|
|
| 40, 9
| -6, 5
| -5, 6
| 89, 5
| | июнь
| -34, 0
| 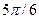
| 29, 4
| -17
| -53, 8
| -17
| 29, 4
| -37, 9
|
| -34
| -43, 6
|
| -25, 5
| -28, 1
| | июль
| -91, 0
| 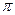
|
|
| -80, 0
| -91
|
| -119, 5
|
|
| -132, 2
| -91
| 0, 0
| -196, 3
| | август
| -181, 0
| 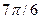
| 156, 7
| 90, 5
| -98, 9
| -90, 5
| -156, 7
| -154, 2
|
|
| -148, 5
| 90, 5
| 135, 7
| -100, 0
| | сентябрь
| 14, 0
| 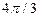
| -7
| -12, 1
| -105, 3
| -7
| 12, 1
| -121, 2
|
|
| -108, 4
| -7
| 6, 1
| -92, 9
| | октябрь
| -93, 0
| 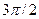
|
|
| -97, 5
|
|
| -58, 1
|
| -93
| -63, 8
| -93
| 0, 0
| -127, 9
| | ноябрь
| -61, 0
| 
| -30, 5
| 52, 8
| -77, 6
| 30, 5
| 52, 8
| -22, 3
|
|
| -35, 0
| 30, 5
| -26, 4
| 13, 5
| | декабрь
| 416, 0
| 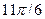
| 360, 3
| -208
| -51, 0
|
| -360, 3
| -35, 1
|
| -416
| -29, 3
| -208
| -312, 0
| -13, 8
| |
|
-153, 0
|
|
-153
|
|
-24, 7
|
-153
|
|
-64, 2
|
-153
|
|
-51, 4
|
-153
|
|
-115, 4
| | январь
| | февраль
| -110, 0
| 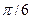
| -95, 3
| -55
| -5, 9
| -55
| -95, 3
| -41, 0
|
| -110
| -67, 0
|
| -82, 5
| -18, 4
| | март
| 71, 0
| 
| 35, 5
| 61, 5
| 0, 5
| -35, 5
| 61, 5
| -35, 6
| -71
|
| -28, 2
| -35, 5
| -30, 7
| -12, 6
| | апрель
| -463, 0
| 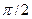
|
| -463
| -7, 3
|
|
| -8, 3
|
|
| 37, 9
| -463
| 0, 0
| -26, 2
| | май
| -150, 0
| 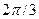
|
| -129, 9
| -27, 1
|
| 129, 9
| 8, 0
| -150
|
| 40, 9
|
| 65, 0
| 89, 5
| | июнь
| -301, 0
| 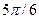
| 260, 7
| -150, 5
| -53, 8
| -150, 5
| 260, 7
| -17, 7
|
| -301
| -43, 6
| 150, 5
| -225, 7
| -28, 1
| | июль
| -379, 0
| 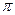
|
|
| -80, 0
| -379
|
| -79, 0
|
|
| -132, 2
| -379
| 0, 0
| -196, 3
| | август
| -358, 0
| 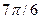
| 310, 0
|
| -98, 9
| -179
| -310, 0
| -134, 0
|
|
| -148, 5
|
| 268, 5
| -100, 0
| | сентябрь
| -193, 0
| 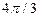
| 96, 5
| 167, 1
| -105, 3
| 96, 5
| -167, 1
| -141, 4
| -193
|
| -108, 4
| 96, 5
| -83, 6
| -92, 9
| | октябрь
| -170, 0
| 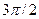
|
|
| -97, 5
|
|
| -98, 5
|
| -170
| -63, 8
| -170
| 0, 0
| -127, 9
| | ноябрь
| -219, 0
| 
| -109, 5
| 189, 7
| -77, 6
| 109, 5
| 189, 7
| -42, 5
|
|
| -35, 0
| 109, 5
| -94, 8
| 13, 5
| | декабрь
| -219, 0
| 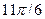
| -189, 7
| 109, 5
| -51, 0
| -109, 5
| 189, 7
| -14, 9
|
|
| -29, 3
| 109, 5
| 164, 2
| -13, 8
| | Итого
| -1886
| -
| 995, 5
| 812, 0
| -1884, 5
| -709, 5
| -740, 4
| -1926, 4
|
| -69
| -1886, 0
| -576, 4
| 171, 5
| -2423, 2
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
Таблица 31 − Распределение дисперсии между гармониками
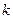
| 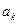
| 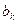
| 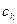
| Вклад в дисперсию
| Вклад, %
| | отдельный
| суммарный
| |
| 27, 7
| 45, 1
| 1400, 7
| 9 80910, 2
| 42, 3
| 42, 3
| |
| -39, 4
| -41, 1
| 1620, 8
| 1 313 472, 0
| 56, 6
| 98, 9
| |
| 12, 8
| -5, 8
| 98, 7
| 4 874, 8
| 0, 2
| 99, 1
| |
| -6, 4
| 19, 1
| 202, 9
| 20 581, 2
| 0, 9
| 100, 0
| | Итого
| -
| -
| -
| 2 319 838, 2
| 100, 0
| -
|
Результаты расчётов свидетельствуют о том, что вторая гармоника наилучшим образом описывает исследуемый процесс.
11. Периодическая модель имеет вид:
 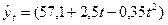 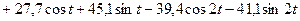 , а прогноз можно осуществлять, используя формулу: , а прогноз можно осуществлять, используя формулу:
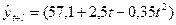 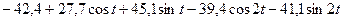 . .
Прогноз на январь 2012 года будет составлять:
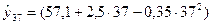 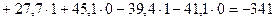 . .
Прогноз на февраль 2012 года:
  . .
Популярное:
|

