Выбор наилучшей математической модели для осуществления прогноза и доверительные интервалы прогноза
Для выбора наилучшей математической модели развития изучаемого явления применяется средняя квадратическая ошибка:
 , ,
где 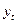 − фактическое значение ряда; − фактическое значение ряда;
 − выравненное значение ряда; − выравненное значение ряда;
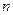 − длина ряда; − длина ряда;
 − число параметров уравнения. − число параметров уравнения.
По минимальной величине средней квадратической ошибки определяют наилучшую модель развития динамического ряда и осуществляют прогноз.
В дополнении к точечному прогнозу определяют доверительные интервалы прогноза. Доверительный интервал определяется по формуле
 , ,
где 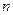 − длина временного ряда; − длина временного ряда;
 − период упреждения; − период упреждения;
 − точечный прогноз на момент − точечный прогноз на момент  ; ;
 − значение − значение 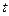 -статистики Стьюдента; -статистики Стьюдента;
 − средняя квадратическая ошибка прогноза. − средняя квадратическая ошибка прогноза.
Предположим, что тренд характеризуется прямой:
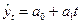
В связи с тем, что параметры уравнения определяются по выборочной совокупности, то они содержат погрешность. Погрешность параметра  приводит к вертикальному сдвигу прямой, а параметра приводит к вертикальному сдвигу прямой, а параметра  − к изменению угла наклона прямой относительно оси абсцисс. Учитывая эти погрешности дисперсию − к изменению угла наклона прямой относительно оси абсцисс. Учитывая эти погрешности дисперсию 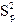 можно представить в виде: можно представить в виде:
 , ,
где  − дисперсия отклонений фактических наблюдений от расчётных; − дисперсия отклонений фактических наблюдений от расчётных;
 − время упреждения, для которого делается экстраполяция; − время упреждения, для которого делается экстраполяция;
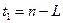 ; ;
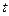 − порядковый номер уровней ряда, − порядковый номер уровней ряда,  ; ;
 − порядковый номер уровня, стоящего в середине ряда, − порядковый номер уровня, стоящего в середине ряда,  . .
Доверительный интервал можно представить в виде:
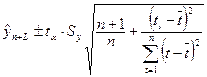
Обозначим корень в представленной формуле через 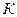 . Значение . Значение 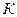 зависит только от зависит только от 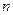 и и  , то есть от длины ряда и периода упреждения. Поэтому можно составить таблицы значений , то есть от длины ряда и периода упреждения. Поэтому можно составить таблицы значений 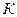 или или  . Тогда интервальная оценка будет иметь вид: . Тогда интервальная оценка будет иметь вид:
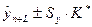
Аналогичное выражение, можно получить для полинома второго порядка:
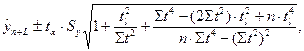
или
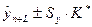 . .
Дисперсия отклонений фактических наблюдений от расчётных определяется выражением:
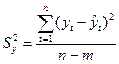 , ,
где 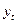 − фактические значения уровней ряда, − фактические значения уровней ряда,
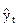 − расчётные значения уровней ряда, − расчётные значения уровней ряда,
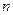 − длина временного ряда, − длина временного ряда,
 − число оцениваемых параметров выравнивающей кривой. − число оцениваемых параметров выравнивающей кривой.
Таким образом, ширина доверительного интервала зависит от уровня значимости, периода упреждения, среднего квадратического отклонения от тренда и степени полинома. Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении 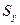 . .
Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяют аналогичным образом. Отличие состоит в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используют не сами значения уровней временного ряда, а их логарифмы. По такой же схеме могут быть определены доверительные интервалы для ряда кривых, имеющих асимптоты, в случае, если значение асимптоты известно (например, для модифицированной экспоненты).
В таблице 21 приведены значения   в зависимости от длины временного ряда в зависимости от длины временного ряда 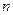 и периода упреждения и периода упреждения  для прямой и параболы. Очевидно, что при увеличении длины рядов ( для прямой и параболы. Очевидно, что при увеличении длины рядов ( 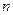 ) значения ) значения  уменьшаются, с ростом периода упреждения уменьшаются, с ростом периода упреждения  значения значения  увеличиваются. При этом влияние периода упреждения неодинаково для различных значений увеличиваются. При этом влияние периода упреждения неодинаково для различных значений 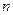 : чем больше длина ряда, тем меньшее влияние оказывает период упреждения : чем больше длина ряда, тем меньшее влияние оказывает период упреждения  . .
Таблица 21 − Значения  для оценки доверительных интервалов прогноза на основе линейного тренда и параболического тренда при доверительной вероятности 0, 9 (7). для оценки доверительных интервалов прогноза на основе линейного тренда и параболического тренда при доверительной вероятности 0, 9 (7).
Длина ряда ( 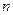 ) )
| Линейный и экспоненциальный тренды
| Длина ряда ( 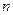 ) )
| Параболический тренд
| период упреждения (  ) )
| период упреждения (  ) )
| |
|
|
|
|
|
| |
| 2, 6380
| 2, 8748
| 3, 1399
|
| 3, 948
| 5, 755
| 8, 152
| |
| 2, 4631
| 2, 6391
| 2, 8361
|
| 3, 459
| 4, 754
| 6, 461
| |
| 2, 3422
| 2, 4786
| 2, 6310
|
| 3, 144
| 4, 124
| 5, 408
| |
| 2, 2524
| 2, 3614
| 2, 4827
|
| 2, 926
| 3, 695
| 4, 698
| |
| 2, 1827
| 2, 2718
| 2, 3706
|
| 2, 763
| 3, 384
| 4, 189
| |
| 2, 1274
| 2, 2017
| 2, 2836
|
| 2, 636
| 3, 148
| 3, 808
| |
| 2, 0837
| 2, 1463
| 2, 2155
|
| 2, 536
| 2, 965
| 3, 516
| |
| 2, 0462
| 2, 1000
| 2, 1590
|
| 2, 455
| 2, 830
| 3, 286
| |
| 2, 0153
| 2, 0621
| 2, 1131
|
| 2, 386
| 2, 701
| 3, 100
| |
| 1, 9883
| 2, 0292
| 2, 0735
|
| 2, 330
| 2, 604
| 2, 950
| |
| 1, 9654
| 2, 0015
| 2, 0406
|
| 2, 280
| 2, 521
| 2, 823
| |
| 1, 9455
| 1, 9776
| 2, 0124
|
| 2, 238
| 2, 451
| 2, 717
| |
| 1, 9280
| 1, 9568
| 1, 9877
|
| 2, 201
| 2, 391
| 2, 627
| |
| 1, 9117
| 1, 9375
| 1, 9654
|
| 2, 169
| 2, 339
| 2, 549
| |
| 1, 8975
| 1, 9210
| 1, 9461
|
| 2, 139
| 2, 293
| 2, 481
| |
| 1, 8854
| 1, 9066
| 1, 9294
|
| 2, 113
| 2, 252
| 2, 422
| |
| 1, 8738
| 1, 8932
| 1, 9140
|
| 2, 090
| 2, 217
| 2, 371
| |
| 1, 8631
| 1, 8808
| 1, 8998
|
| 2, 069
| 2, 185
| 2, 325
| |
| 1, 8538
| 1, 8701
| 1, 8876
|
| 2, 049
| 2, 156
| 2, 284
|
Например: На основе построенных математических моделей развитияпо данным о числе разводов в Хабаровском крае (таблица 18) определить наилучшую модель развития динамического ряда и осуществить прогноз.
Решение
Таблица 22 − Расчётная таблица
| Год
| Модели
| Квадрат отклонений 
| |
| линей-ный тренд
| парабо-ла второго порядка
| экспо-нента
| линейный тренд
| парабола второго порядка
| экспонента
| |
| 9 619, 9
| 9 777, 1
| 7 856, 5
| 7 639 143, 0
| 8 533 023, 0
| 1 000 892, 0
| |
| 9 545, 5
| 9 918, 7
| 7 872, 2
| 2 183 006, 0
| 3 424 914, 0
| 38 350, 8
| |
| 9 471, 1
| 10 017, 0
| 7 887, 9
| 39 561, 2
| 120 401, 7
| 3 175 814, 0
| |
| 9 396, 7
| 10 072, 2
| 7 903, 7
| 2 680 751, 0
| 925 164, 4
| 9 798 763, 0
| |
| 9 322, 3
| 10 084, 1
| 7 919, 5
| 72 738, 1
| 242 181, 9
| 2 797 197, 0
| |
| 9 247, 9
| 10 052, 9
| 7 935, 4
| 3 440 654, 0
| 7 075 137, 0
| 294 159, 4
| |
| 9 173, 5
| 9 978, 5
| 7 951, 2
| 6 192 632, 0
| 10 847 307, 0
| 1 603 372, 0
| |
| 9 099, 1
| 9 860, 9
| 7 967, 2
| 3 069 854, 0
| 6 319 972, 0
| 384 590, 7
| |
| 9 024, 7
| 9 700, 2
| 7 983, 1
| 609 492, 0
| 2 120 532, 0
| 68 070, 9
| |
| 8 950, 3
| 9 496, 3
| 7 999, 1
| 692 723, 0
| 1 899 636, 0
| 14 144, 3
| |
| 8 875, 9
| 9 249, 2
| 8 015, 1
| 310 138, 0
| 865 196, 3
| 92 369, 6
| |
| 8 801, 5
| 8 958, 9
| 8 031, 1
| 1 328 256, 0
| 1 715 745, 0
| 146 011, 5
| | Итого
| -
| -
| -
| 28 258 950, 4
| 44 089 211, 0
| 19 413 735, 0
|
Рассчитаем среднюю квадратическую ошибку:
 . .
Линейный тренд − 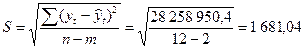 . .
Парабола второго порядка − 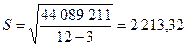 . .
Экспонента −  . .
Наименьшая квадратическая ошибка получилась у экспоненциальной формы тренда:
 . .
Прогноз на 2011, 2012 и 2013 годы (  , ,  , ,  ): ):
 ; ;
 ; ;
 (таблица 22) (таблица 22)
Рассчитаем доверительные интервалы по формуле
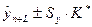
Таблица 23 − Результаты прогноза числа разводов в Хабаровском крае
| Год
| 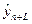
| 
| 
| Доверительный интервал прогноза 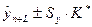
| | нижняя граница
| верхняя граница
| |
| 7 840, 7
| 2, 1274
|
| 4876, 7
|
| |
| 7 824, 9
| 2, 2017
|
| 4756, 9
|
| |
| 7 809, 3
| 2, 2836
|
| 4627, 3
|
|
Прогнозные данные свидетельствуют о том, что наметилась позитивная тенденция снижения числа разводов (таблица 23). Ежегодное число разводов будет сокращаться в среднем на 16 разводов (около 1%).
Популярное:
|

