
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Понятия скорости и ускорения
Кинематика Основные понятия кинематики
Раздел механики, изучающий движение материальных тел в пространстве и времени без рассмотрения причин, вызывающих это движение, называется кинематикой. Характер движения одного и того же тела может быть различным в зависимости от того, по отношению к какому телу это движение рассматривается. Поэтому для описания движения необходимо условиться, относительно какого другого тела будет отсчитываться перемещение данного тела. Выбранное для этой цели тело называется телом отсчета. Жестко связанная с этим телом система координат совместно с эталоном длины и часами образуют систему отсчета.
Системы отсчета можно подразделить на инерциальные и неинерциальные. Инерциальная система жестко связана с опорным телом, на которое не действуют внешние силы (или эти силы пренебрежимо малы). В инерциальных системах справедливы и выполняются законы классической механики Ньютона. Тел, на которые не действуют внешние силы, в природе весьма много, поэтому и инерциальных систем отсчета также очень много. Друг относительно друга инерциальные системы отсчета либо неподвижны, либо движутся с постоянными по величине и направлению скоростями. Если в какой либо инерциальной системе на некоторое тело действует сила и эта сила вызывает ускоренное движение тела, то и в любой другой инерциальной системе и сила и ускорение будут такими же. В неинерциальных системах отсчета все совсем не так, т.е. при переходе из одной неинерциальной системы в другую изменяются и величины сил и ускорения тел. Рассмотрим вначале движение самого простого объекта классической механики – материальной точки. По определению, материальная точка это тело, размеры которого пренебрежимо малы по сравнению с масштабами движения. Пространственное положение и движение материальной точки может быть задано в декартовой системе координат, которая жестко связана с телом, на которое не действуют силы. Положение точки М в этой системе характеризуется координатами x, y, z (рис.1):
где
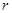 и два угла j и q, которые составляет радиус-вектор с осями y и z. и два угла j и q, которые составляет радиус-вектор с осями y и z.
Рассмотрим теперь движение материальной точки. Совокупность последовательных положений, занимаемых точкой в процессе ее движения, образует в пространстве линию, называемую траекторией движущейся точки (рис.2).
Пусть движущаяся точка в момент времени t находится в положении М1 и ее радиус-вектор Длина дуги М1М2=
Вектор перемещения характеризует изменение положения точки М в пространстве. Вектор перемещения характеризует как направление перемещения так и величину перемещения. Модуль вектора перемещения Рис.5
|
Из уравнений (4) и (5) следует связь между величинами мгновенной скорости 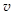 и угловой скорости w
и угловой скорости w
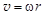 .
.
Так как линейная и угловая скорости являются векторами, то связь между ними можно записать также в форме векторного произведения
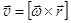 .
.
Рассмотрим теперь равномерное вращательное движение.
При таком движении величина угловой скорости остается постоянной w = const, и из формулы (5) следует
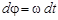 . (6)
. (6)
Чтобы найти связь w и j за конечный промежуток времени необходимо проинтегрировать выражение (6)
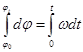 .
.
Так как w = const, то ее можно вынести за знак интеграла и в результате интегрирования получи
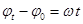 , или
, или 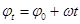 ,
,
где 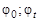 – угол поворота в начальный момент времени и в момент времени t.
– угол поворота в начальный момент времени и в момент времени t.
Эта формула верна только для вращательного движения по окружности с постоянной угловой скоростью.
Для такого движения можно ввести понятие периода обращения Т. Период Т – это время, затрачиваемое на один полный оборот. Величина обратная периоду называется частотой n. В системе СИ период измеряется в секундах, а частота в Герцах (Гц). Один Герц соответствует одному обороту за секунду.
За время, равное T, материальная точка совершает полный оборот, т.е. проходит угол j = 2p (рад). Тогда, из соотношения (6) получим:
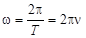 ,
,
где n – частота вращения выраженная в Гц.
Законы Ньютона
I закон Ньютона. Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
I закон Ньютона является определением инерциальной системы отсчета. Согласно этому закону, любая система координат жестко связанная с любым массивным телом, на которое не действуют внешние силы (или эти силы пренебрежимо малы), является инерциальной системой отсчета. Только в инерциальных системах отсчета справедливы и выполняются второй и третий классические законы Ньютона.
II закон Ньютона. Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела:
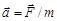 или
или 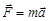 .
.
Так как ускорение 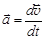 , а скорость
, а скорость 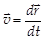 , то II закон Ньютона можно записать и в следующих математических редакциях:
, то II закон Ньютона можно записать и в следующих математических редакциях:
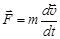
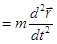 .
.
В классической механике Ньютона масса тела – величина постоянная, поэтому ее можно внести под знак производной и II закону придать еще одну математическую редакцию:
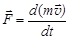 .
.
Если на тело действуют не одна, а несколько сил, то ускорение будет сообщать векторная сумма этих сил (равнодействующая всех сил):
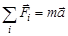 .
.
Второй закон Ньютона имеет экспериментальное обоснование.
III закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия; силы, с которыми тела действуют друг на друга, всегда равны по величине, направлены по одной прямой и противоположны по направлению.
Силы взаимодействия двух тел приложены к разным телам и поэтому не компенсируют друг друга.
Обозначая силу, действующую на первое тело со стороны второго, через 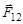 , а силу, действующую на второе тело со стороны первого, через
, а силу, действующую на второе тело со стороны первого, через 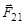 , запишем III закон Ньютона в следующей математической редакции:
, запишем III закон Ньютона в следующей математической редакции:
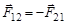 .
.
Знак минус показывает, что силы имеют противоположные направления.
Потенциальное поле сил
Любое тело подвержено воздействию сил со стороны окружающих его тел. При изменении положения данного тела в пространстве, сила, с которой действуют на него окружающие тела, будет меняться. В каждой точке пространства на тело действует определенная, характерная для данной точки, сила. Поэтому говорят, что тело находится в поле сил. Например, тело вблизи поверхности Земли находится в поле сил тяжести. Сама Земля находится в поле сил тяготения, создаваемого другими небесными телами. Можно привести и другие примеры полей сил. Например, в пространстве вокруг неподвижных электрически заряженных тел имеется электростатическое поле сил.
Различают силы консервативные (или потенциальные) и неконсервативные.
Силы , действующие на тело, называются консервативными (потенциальными), если работа этих сил при перемещении тела не зависит от формы пути, а определяется только начальным и конечным положением тела в пространстве.
Силы , действующие на тело, называются неконсервативными, если работа сил зависит от формы пути перемещения тела между двумя конкретными точками пространства.
Если в физической системе действуют только консервативные силы, то система называется консервативной; в противном случае – неконсервативной.
Так как работа консервативных сил зависит только от положения начальной и конечной точек перемещения, то на замкнутом пути, когда начальная и конечная точка совпадают, работа перемещения будет равняться нулю. Математически это выражается следующим образом:
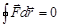 .
.
Примером консервативных сил является поле сил тяжести. Действительно, если тело в поле сил тяжести перемещать по замкнутой траектории, например, вначале поднять на некоторую высоту, а затем опустить в исходную точку, то работа этого перемещения будет равна нулю, На подъем затрачивается некоторая работа (т.е. работа в этом случае отрицательна), а при опускании тела такая же работа возвращается (т.е. работа положительна).
Примером неконсервативных сил являются силы трения. Действительно, если на тело действуют силы трения и тело перемещается между двумя точками пространства, то на перемещение придется затратить некоторое количество работы, которая превратиться в тепло. На перемещение тела в исходную точку вновь придется затратить работу. Следовательно, общий расход механической работы на перемещение по замкнутому пути не будет равен нулю откуда следует, что силы трения неконсервативны.
Энергия.
Сила трения
Силы трения весьма разнообразны. Так, например, силы трения возникают при движении одного тела по поверхности другого. Силы трения возникают также, если тело имеет форму шара или цилиндра и перемещается за счет качения. В этом случае говорят о трении качения. Если тело движется в жидкости или газе то также возникают силы трения, препятствующие движению тела. Эти силы зависят от формы, размеров и скорости движения тела по отношению к среде. Если в жидкости или в газе два соседних слоя двигаются с разными скоростями, то между ними также действует сила трения. В этом случае явление называется внутренним трением.
Трение между поверхностями двух твердых тел при отсутствии какой-либо прослойки между ними, например, смазки, называют сухим трением.
Далее рассматривается только сухое трение. Другие силы трения рассматриваются в последующих разделах курса физики.
В случае сухого трения сила трения возникает не только при скольжении одного тела по поверхности другого, но также при попытках вызвать такое скольжение (т.е. при попытке сдвинуть тело с места). Иначе говоря, если приложенная к телу сила меньше некоторой величины, то движение вызвать невозможно. Силу, действующую между поверхностями соприкосновения в этом случае, называют силой трения покоя. Если величина приложенной к телу силы больше этой величины, то возникает скольжение тела по поверхности другого тела. Сила трения, если тело движется, направлена противоположно скорости тела. Как следует из экспериментальных исследований, величина силы трения в этом случае практически не зависит от скорости тела и площади соприкасающихся поверхностей, но зависит от силы, с которой трущиеся поверхности «прижимаются» друг к другу и от свойств самих поверхностей (например, шероховатости). Движущееся тело «прижимается» силой нормального давления, т.е. силой с которой движущееся тело действует на поверхность того тела, по которому происходит скольжение. Термин – нормальное давление подчеркивает то обстоятельство, что эта сила нормальна (перпендикулярна) поверхности скольжения. По III закону Ньютона и поверхность скольжения, действует на движущееся тело с такой же по величине и противоположно направленной силой. Эта сила называется реакцией опоры. Поэтому величина силы трения равна:
Fтр = mN,
где m – коэффициент трения, зависящий от свойств соприкасающихся поверхностей; N – реакция опоры Отметим еще раз, что последняя формула определяет только величину силы трения, но не направление силы трения, которое всегда противоположно скорости движения тела.
В качестве примера рассмотрим соскальзывание тела массы m с наклонной плоскости с углом при основании α (рис.8). На тело действуют три силы: сила тяжести 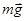 , сила трения
, сила трения 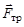 и сила реакции опоры
и сила реакции опоры 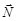 . Результирующая этих трех сил согласно II закону Ньютона вызывает движение тела с ускорением
. Результирующая этих трех сил согласно II закону Ньютона вызывает движение тела с ускорением 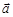 вдоль наклонной плоскости:
вдоль наклонной плоскости:
Рис.8
|
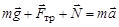 .
.
Проекции векторов на оси координат, указанные на рис.8, дают два уравнения:
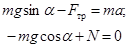 .
.
Из второго уравнения определяем реакцию опоры и затем величину силы трения:
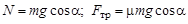 .
.
Первое уравнение позволяет рассчитать ускорение тела:
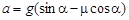 .
.
При малых углах наклона a тело будет оставаться неподвижным. Для этого необходимо чтобы:
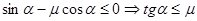 .
.
Таким образом, при 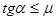 тело будет неподвижным на наклонной плоскости, т.е. сила трения покоя в этом случае достаточна, чтобы удержать тело и не позволить ему соскальзывать с наклонной плоскости.
тело будет неподвижным на наклонной плоскости, т.е. сила трения покоя в этом случае достаточна, чтобы удержать тело и не позволить ему соскальзывать с наклонной плоскости.
Центр масс твердого тела
Рассмотрим твердое тело произвольной геометрии и распределения масс. Разобьем мысленно тело на малые (не обязательно одинаковые) элементы и пронумеруем их. Допустим, что к некоторому элементу тела с номером i и массой Dmi приложена внешняя сила 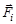 и кроме этого действуют внутренние силы со стороны остальных элементов тела
и кроме этого действуют внутренние силы со стороны остальных элементов тела 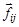 . Под воздействием результирующей всех сил, приложенных к рассматриваемому элементу тела, будет происходить движение в соответствии со II законом Ньютона:
. Под воздействием результирующей всех сил, приложенных к рассматриваемому элементу тела, будет происходить движение в соответствии со II законом Ньютона:
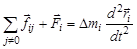 ,
,
где 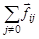 – сумма всех внутренних сил, действующих на элемент c номером i со стороны всех остальных элементов тела;
– сумма всех внутренних сил, действующих на элемент c номером i со стороны всех остальных элементов тела;
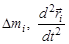 –масса и ускорение элемента тела с номером i.
–масса и ускорение элемента тела с номером i.
Проведем суммирование по всем элементам тела. При суммировании внутренние силы взаимно сокращаются, так как всякой силе, действующей на элемент тела i со стороны элемента j, согласно III закону Ньютона, имеется равная и противоположно направленная сила, действующая на элемент j со стороны элемента i. Сумма всех внешних сил (результирующая сила) будет равна:
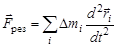 . (13)
. (13)
Рассмотрим теперь точку, радиус-вектор которой
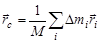 ,
,
где M – масса всего тела. Назовем эту точку центром масс тела. Смысл этого термина выясняется ниже.
Дважды продифференцируем последнее выражение по времени:
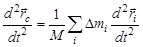 . (14)
. (14)
Из сравнения (13) и (14) следует, что
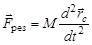 .
.
Так как 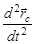 , является ускорением центра масс тела, то последнее соотношение означает, что центр масс движется в соответствии со II законом Ньютона, причем движение происходит так, как если бы вся масса тела была сосредоточена в точке центра масс.
, является ускорением центра масс тела, то последнее соотношение означает, что центр масс движется в соответствии со II законом Ньютона, причем движение происходит так, как если бы вся масса тела была сосредоточена в точке центра масс.
Рассмотрим теперь замкнутую (изолированную) систему тел. В замкнутой системе 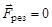 (сумма всех внешних сил равна нулю), поэтому центр масс будет либо двигаться прямолинейно и равномерно либо оставаться в покое. Внутренние силы, при этом, между отдельными частями системы могут и не равняться нулю, но как только что было показано, они не могут повлиять на движение центра масс, но влияют на движение отдельных тел, составляющих систему.
(сумма всех внешних сил равна нулю), поэтому центр масс будет либо двигаться прямолинейно и равномерно либо оставаться в покое. Внутренние силы, при этом, между отдельными частями системы могут и не равняться нулю, но как только что было показано, они не могут повлиять на движение центра масс, но влияют на движение отдельных тел, составляющих систему.
Заметим также, что вместо термина «центр масс» иногда используется термин «центр инерции».
В ряде случаев задача отыскания положения центра масс может быть упрощена. Так, например, если рассматривается движение твердого тела, обладающего тем или иным типом симметрии, то можно указать на пространственное положение центра масс и без детальных расчетов. Приведем некоторые примеры: - центр масс однородного по плотности шара совпадает с его центром; центр масс тонкого однородного по плотности стержня расположен на его середине; три материальные точки одинаковой массы, расположенные в вершинах жесткого равностороннего треугольника имеют центр масс в точке пересечения биссектрис внутренних углов треугольника и т.д.
Решение задач по определению положения центра масс некоторого тела может быть упрощена, если находить отдельно все три проекции радиус-вектора 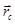 центра масс.
центра масс.
В качестве примера, рассмотрим два шара массами m1 и m2 находящимися на фиксированном расстоянии l друг от друга и найдем центр масс этой системы (рис.9). Каждый шар можно рассматривать как материальную точку с массой, расположенной в его центре.
 Рис.9
Рис.9
|
Направим ось X вдоль прямой проходящей через центры шаров, а начало координат поместим на расстоянии а от левого шара. Тогда координату Xc центра масс можно записать в виде:
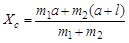 .
.
Если поместить начало координат в центр первого шара (т.е. положить а = 0), то выражение для Xc будет иметь более простой вид
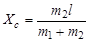 .
.
В частном случае, когда m1 = m2, Хс = l/2, т.е. для одинаковых шаров центр масс будет находиться в точке, расположенной посередине между шарами.
Контрольные вопросы и задачи
1. Как формулируется первый закон Ньютона?
2. Сформулируйте второй закон Ньютона и напишите его формулу.
3. Сформулируйте третий закон Ньютона и напишите его формулу.
4. Какая физическая величина называется импульсом силы? Напишите формулу, определяющую импульс силы. В каких единицах системы СИ измеряется импульс силы?
5. Какая физическая величина называется импульсом тела? Напишите формулу, определяющую импульс тела. В каких единицах системы СИ измеряется импульс тела?
6. Как связана элементарная работа с вектором силы 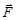 и вектором элементарного перемещения
и вектором элементарного перемещения 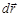 ? В каких единицах в системе СИ измеряется работа?
? В каких единицах в системе СИ измеряется работа?
7. Какая физическая величина называется мощностью? В каких единицах в системе СИ измеряется мощность?
8. Что называется консервативной физической системой? Какими свойствами обладает консервативная система?
9. Построить график зависимости от времени кинетической, потенциальной и полной энергии камня массой в 1 кг, брошенного вертикально вверх с начальной скоростью 9, 8 м/с, для промежутка времени 0-1 с через каждые 0, 2 с.
10. Тело массой 1 кг двигается по горизонтальной поверхности. Коэффициент трения m = 0, 1. Чему равна сила трения, действующая на тело? (ускорение свободного падения принять равным 10 м/с2)
11. Железнодорожный составмассы М = 3000 т. двигается с постоянной скоростью v = 72 км/ч. Коэффициент трения равен 0, 01. Чему равна сила тяги локомотива? Какую мощность развивает локомотив?
12. Цепочка массы m = 2 кг и длины l = 2 м висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.
15. Лодка находиться далеко от берега озера. Человек массы m = 70 кг перешел с носа лодки на корму. Длина лодки l = 5 м; масса лодки 210 кг. На какое расстояние при этом переместилась лодка?
16. Найти положение центра масс системы, состоящей из малых по размерам трех тел. Два из них имеют массы по m = 2 кг и находятся на расстоянии 60 см друг от друга. Третье тело имеет массу m = 4 кг и находится на расстоянии 50 см от каждого из первых двух.
17. Клеть шахтного ствола (шахтная клеть является разновидностью лифта), массой 3 т, поднимается с постоянной скоростью на высоту 200 м. Коэффициент полезного действия подъемного механизма 80 %. Время подъема составляет 3 мин. Чему равна работа, совершаемая подъемным механизмом и чему равна мощность, потребляемая подъемным механизмом?
18. Вагонетку массы 1, 5 т. при буксировке тянут горизонтально с постоянной скоростью 5 м/с. Натяжение троса равно 19, 5 кН. Какая работа совершается при перемещении вагонетки на расстояние 1, 5 км? Определить коэффициент трения и мощность, развиваемую при буксировке.
19. Для погрузки угля в вагоны применяется ленточный транспортер, который перемещает уголь вверх по наклону на высоту 5 м. В минуту погрузчик доставляет 12 т угля к товарным вагонам. Какую работу совершает транспортер за 5 мин.?
20. Вагон с углем, имеющий массу 40 т, движется со скоростью 2 м/c навстречу к неподвижному вагону такой же массы и сталкивается с ним. Определить максимальное сжатие пружины буферов вагонов, считая деформацию пружины упругой, если известно, что под действием силы F = 200 кН сжатие пружины составляет 1 см.
Главные оси инерции
Момент инерции твердого тела произвольной формы и распределения масс зависит от ориентации оси вращения. Допустим, что ось проходит через центр масс тела (центр инерции). Найдем такую ориентацию оси, для которой момент инерции максимален. Далее, как доказывается в теоретической механике, существует также ось перпендикулярная найденной, и проходящая через центр масс, для которой момент импульса твердого тела будет минимален. Для третьей оси, ортоганальной к первым двум, момент импульса в общем случае имеет величину промежуточную между максимальным и минимальным значениями. Введенные таким образом оси вращения называются главными осями инерции. Моменты инерции относительно этих осей не обязательно отличаются друг от друга по величине. Действительно, если однородное по плотности твердое тело обладает той или иной симметрией, то некоторые главные моменты инерции могут равняться друг другу. Так, например, однородный по плотности шар имеет три равных момента инерции относительно главных осей, каждый из которых равен: 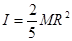 , где M, R - масса и радиус шара.
, где M, R - масса и радиус шара.
Однородный куб с массой М и длиной ребра 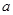 имеет также три равных момента инерции относительно главных осей инерции
имеет также три равных момента инерции относительно главных осей инерции 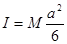 . Главные оси инерции перпендикулярны граням куба и проходят через центр куба..
. Главные оси инерции перпендикулярны граням куба и проходят через центр куба..
Тонкий однородный по плотности диск имеет максимальный по величине момент инерции относительно оси, проходящей через центр диска перпендикулярно его плоскости, а также два других главных момента инерции равных друг другу.
Приведем также пример тела, когда все три момента инерции относительно главных осей инерции различны - однородный по плотности параллелепипед с отличающимися по длине ребрами.
Твердого тела
Рис.16
|
Рассмотрим твердое тело, которое может вращаться вокруг неподвижной в пространстве оси вращения ОО (рис.16). Разобьем все тело на элементарные массы Dmi. В общем случае к каждой элементарной массе может быть приложена некоторая внешняя сила 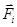 . Составляющая силы
. Составляющая силы 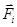 , вызывающая вращение должна быть направлена по касательной к окружности, по которой движется элементарная масса. Остальные две составляющие внешней силы вызывают либо деформацию фиксированной в пространстве оси вращения, либо определяют нагрузку на опоры оси вращения, но вращения не вызывают. Обозначим равнодействующую всех внешних сил приложенных к некоторой элементарной массе Dmi и вызывающих вращение через
, вызывающая вращение должна быть направлена по касательной к окружности, по которой движется элементарная масса. Остальные две составляющие внешней силы вызывают либо деформацию фиксированной в пространстве оси вращения, либо определяют нагрузку на опоры оси вращения, но вращения не вызывают. Обозначим равнодействующую всех внешних сил приложенных к некоторой элементарной массе Dmi и вызывающих вращение через 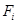 (рис.16). Внутренние силы, действующие между элементарными массами твердого тела, учитывать не будем, так как при последующем суммировании, как сами силы, так и их моменты взаимно сокращаются (III закон Ньютона! ).
(рис.16). Внутренние силы, действующие между элементарными массами твердого тела, учитывать не будем, так как при последующем суммировании, как сами силы, так и их моменты взаимно сокращаются (III закон Ньютона! ).
По второму закону Ньютона, имеем:
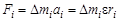 , (18)
, (18)
где 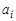 ,
, 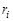 – линейное ускорение и радиус-вектор элементарной массы; e – угловое ускорение вращения тела, как единого целого (
– линейное ускорение и радиус-вектор элементарной массы; e – угловое ускорение вращения тела, как единого целого ( 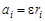 ).
).
Умножим обе части (18) на ri:
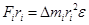 .
.
Так как Firi = DМi по определению является моментом силы, действующим на элемент массы Dmi относительно заданной оси вращения, то следовательно:
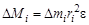 .
.
Суммируя по всем элементарным массам, на которое разбито тело, получим:
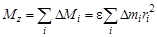 .
.
Величина суммы 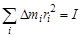 – это момент инерции тела относительно заданной оси вращения, поэтому последнее выражение можно записать в следующей форме:
– это момент инерции тела относительно заданной оси вращения, поэтому последнее выражение можно записать в следующей форме:
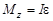 , (19)
, (19)
где 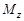 – проекция на заданную ось вращения суммарного момента внешних сил, действующих на твердое тело; e – величина углового ускорения.
– проекция на заданную ось вращения суммарного момента внешних сил, действующих на твердое тело; e – величина углового ускорения.
Напомним, что момент сил относительно заданной оси вращения, является проекцией вектора момента сил на ось вращения. Поэтому, в общем случае, когда ось вращения не фиксирована в пространстве, вращение вызывается не одной проекцией момента сил, а всеми тремя проекциями, т.е. вектором момента сил 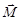 . Поэтому, уравнение (19) можно записать в следующей форме:
. Поэтому, уравнение (19) можно записать в следующей форме:
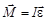 . (20)
. (20)
Добавочно напомним, что момент инерции твердого тела I в общем случае зависит от пространственного положения оси вращения.
Уравнение (20) является основным уравнением динамики вращательного движения . По форме оно сходно с уравнением II закона Ньютона и его иногда называют вторым законом динамики для вращательного движения.
Основное уравнение вращательного движения может быть дано и в иной математической редакции. Для этого вспомним, что угловое ускорение определяется производной от угловой скорости по времени: 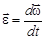 . После подстановки в (20) имеем:
. После подстановки в (20) имеем: 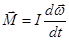 . Если I-const, то внося величину I под знак производной, получим:
. Если I-const, то внося величину I под знак производной, получим:
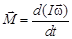 .
.
Выражение, стоящее в скобках является моментом импульса твердого тела 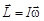 и поэтому основной закон динамики вращательного движения твердого тела можно записать еще в одной математической редакции:
и поэтому основной закон динамики вращательного движения твердого тела можно записать еще в одной математической редакции:
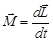 . (21)
. (21)
Законы сохранения
Закон сохранения энергии
Закон сохранения импульса
Рассмотрим систему, состоящую из N тел. Силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними силами будем называть силы, с которыми действуют друг на друга отдельные части системы, а внешними – силы, обусловленные внешними телами, не принадлежащими к системе.
В случае если внешние силы отсутствуют, система называется замкнутой или изолированной. Если сумма всех внешних сил равна нулю, то система называется квазизамкнутой (квазиизолированной).
Импульсом системы, состоящей из N тел, называется векторная сумма импульсов всех тел, образующих систему.
Для суммарного импульса изолированной (замкнутой) системы существует закон сохранения импульса: суммарный импульс замкнутой (изолированной или квазиизолированной) системы остается постоянным:
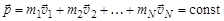 .
.
Закон сохранения импульса является теоретическим следствием законов Ньютона. Покажем это. Рассмотрим физическую систему, состоящую из N тел. Пронумеруем эти тела от i = 1 до i = N. Допустим, что между телами системы действуют внутренние силы 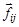 и кроме этого на тела системы действуют внешние силы со стороны тел, не принадлежащих к системе –
и кроме этого на тела системы действуют внешние силы со стороны тел, не принадлежащих к системе – 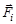 . Напишем II закон Ньютона для каждого тела физической системы:
. Напишем II закон Ньютона для каждого тела физической системы:
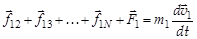 ;
;
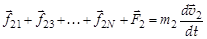 ;
;
……………………………………
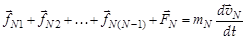 .
.
Проведем суммирование этих соотношений. В левой части равенства получим сумму всех внутренних сил и сумму всех внешних сил. Но на основании III закона Ньютона внутренние силы при сложении взаимно сокращаются, так как каждому действию есть равное и противоположно направленное противодействие, поэтому получим:
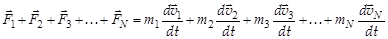 .
.
Сумма всех внешних сил определяет результирующую силу 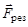 , действующую на всю физическую систему:
, действующую на всю физическую систему:
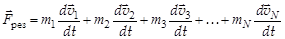 .
.
Теперь допустим, что система замкнута, т.е. внешние силы отсутствуют, или квазизамкнута, т.е. сумма всех внешних сил равна нулю. Тогда имеем:
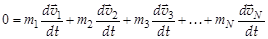 .
.
Внося постоянные массы под знаки производных, получим:
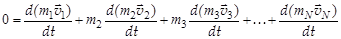 .
.
Так как сумма производных равна производной от суммы то:
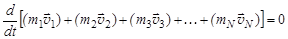 .
.
В этом соотношении производная по времени равна нулю, т.е. выражение в фигурных скобках есть величина постоянная. Легко заметить, что в фигурных скобках стоит сумма импульсов тел системы и, следовательно, сумма импульсов тел системы не изменяется с течением времени, т.е. является величиной постоянной. Это утверждение составляет содержание закона сохранения импульса, относящегося к замкнутой (изолированной), или квазизамкнутой (квазиизолированной) системе.
Рассмотрим некоторые примеры, в которых применяется закон сохранения энергии и импульса:
1. Удар двух абсолютно упругих шаров. Такназывается соударение шаров, при котором механическая энергия тел не переходит в другие, немеханические виды энергии.
При таком соударении кинетическая энергия шаров переходит при столкновении вначале в потенциальную энергию упругой деформации, затем шары возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и шары разлетаются со скоростями, величина и направление которых определяется двумя законами – законом сохранения энергии и законом сохранения импульса. Шары после столкновения будут двигаться с разными скоростями.
Закон сохранения импульса определяет равенство суммарных импульсов шаров до и после столкновения:
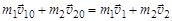 ,
,
где 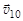 и
и 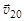 – скорость шаров до столкновения;
– скорость шаров до столкновения; 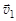 и
и 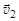 – скорости шаров после столкновения; m1, m2 – массы шаров.
– скорости шаров после столкновения; m1, m2 – массы шаров.
Закон сохранения энергии определяет равенство суммарных кинетических энергий до и после столкновения:
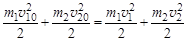 .
.
Решая совместно уравнения, выражающие законы сохранения энергии и импульса, получим для скоростей шаров после столкновения:
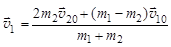 ;
; 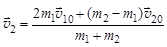 .
.
2. Удар двух абсолютно неупругих шаров характеризуется тем, что кинетическая энергия частично превращается во внутреннюю энергию, приводя к повышению температуры шаров. После удара столкнувшиеся шары движутся вместе с одинаковой скоростью как единое целое. Закон сохранения импульса определяет равенство суммарных импульсов шаров до и после столкновения:
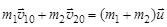 ,
,
где 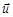 – скорость шаров после столкновения.
– скорость шаров после столкновения.
Оттуда находим скорость шаров после неупругого столкновения:
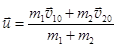 .
.
Количество механической энергии перешедшей во внутреннюю энергию (тепло) равно разности кинетических энергий этих шаров до и после удара:
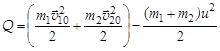 .
.
Всемирное тяготение
Законы Кеплера
Основанием для установления закона всемирного тяготения Ньютону послужили, наряду с законами динамики, носящими его имя, три открытых Кеплером (1571-1630) закона движения планет:
|
|
2. Радиус-вектор, проведенный от Солнца к конкретной планете, отсекает, за равные промежутки времени, равные площади.
3. Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей эллипсов их орбит.
Третий закон Кеплера можно записать в следующей форме:
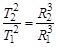 ,
,
где T1и T2 – периоды обращения двух конкретных планет; R1 и R2 – большие полуоси соответствующих эллипсов.
Последнее изменение этой страницы: 2016-08-31; Просмотров: 809; Нарушение авторского права страницы